【题解】BZOJ4669 - 抢夺

题意

给出一个包含 \(n\) 个点和 \(m\) 条边的有向图。点的编号为 \(0\) 到 \(n - 1\)。第 \(i\) 条边 \((u_i, v_i)\) 有其同一时刻最多能容纳的人数 \(c_i\) ，且通过每条边的时间均为 \(1\)。

初始时在源点 \(0\) 有 \(k\) 个人，试求 \(k\) 个人均到达汇点 \(n - 1\) 所需的最小时间。若 \(k = 0\)，则认为需要 \(0\) 个时刻。

\(1 \leq n \leq 10^3, 1 \leq m \leq 5 \times 10^3, 0 \leq k \leq 10^9\)

\(\forall (u, v) \in E,\ 0 \leq u, v < n, 1 \leq c_i \leq 10^9\)

多测，数据不超过 \(10\) 组。

思路

费用流 + 二分答案。

一个显然的思路是将每个点拆成不同时刻的若干点，然后在分层图上跑最大流。事实上这个做法可以 AC 此题的弱化版 P4400 [JSOI2008]Blue Mary的旅行，原因是该题的层数上界较小。但是此题的数据范围太大，会 TLE 30 分。

考虑将每条边的通过时间视为费用，最大能容纳的人数视为容量。贪心的想法是每次都走最短路，但是这样做可能导致若干人汇集到一个点上等待，所以可以考虑从最短路开始，每次在当前有人经过的路径集合中替换或加入路径（均为较短路），遍历到所有可行的方案。

显然答案有单调性，不妨考虑用二分答案实现。每次枚举当前的时间上限 \(t\)，如果在超过时刻 \(t\) 前可以令 \(k\) 个人都到达点 \(n - 1\)，则可以用 \(t\) 更新答案。

假设在残量网络中找到了一条长度为 \(d\)，流量为 \(f\) 的增广路。如果这条增广路不含反向边，显然可以令源点每个时刻都出发 \(f\) 个人走该路径到 \(t\)，即该路径从时刻 \(d\) 开始，在超过时刻 \(t\) 前共可以运输 \((t - d + 1) \cdot f\) 人。

如果该路径含反向边，相当于将这条路径划分给原本的一条较短路和一条新的较短路。此时将 \((t - d + 1) \cdot f\) 人统计进可以运输的总人数，实际上相当于用该反向边的费用撤销了原本的较短路花费的时间。

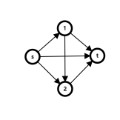
如图，假设此前有人经过路径 \(s, 1, 2, t\)，则当通过路径 \(s, 2, 1, t\) 增广到反向边 \(2, 1\) 时，相当于原本的较短路 \(s, 1, 2, t\) 替换成两条较短路 \(s, 1, t\) 和 \(s, 2, t\)，原本走过 \(1, 2\) 边需要的时间则通过 \(2, 1\) 边撤销。

我们发现上面换最短路的过程和 EK 类似，所以直接用 EK 写即可。时间复杂度为 EK 的复杂度套 \(\log(\textrm{V})\)，其中 \(V\) 为答案值域，可以取 \(10^{12}\)

代码

#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
using namespace std;

typedef long long ll;

const int maxn = 1e3 + 5;
const int maxm = 1e4 + 5;
const int maxk = 5e3 + 5;
const int inf = 0x3f3f3f3f;
const ll flow_max = 1e18;

struct node {
	int to, nxt, w, c;
} edge[maxm];

int n, m, k, s, t;
int cnt = 1, mc;
int ui[maxk], vi[maxk], wi[maxk];
int head[maxn], dis[maxn], pre[maxn];
ll sum, mf, flow[maxn];
bool in_queue[maxn];

void add_edge(int u, int v, int w, int c) {
	cnt++;
	edge[cnt].to = v;
	edge[cnt].nxt = head[u];
	edge[cnt].w = w;
	edge[cnt].c = c;
	head[u] = cnt;
}

void add(int u, int v, int w, int c) {
	add_edge(u, v, w, c);
	add_edge(v, u, 0, -c);
}

bool spfa() {
	queue<int> q;
	memset(dis, 0x3f, (t + 1) * sizeof(int));
	dis[s] = 0;
	flow[s] = flow_max;
	in_queue[s] = true;
	q.push(s);
	while (!q.empty()) {
		int u = q.front();
		q.pop();
		in_queue[u] = false;
		for (int i = head[u]; i; i = edge[i].nxt) {
			int v = edge[i].to;
			if ((dis[v] > dis[u] + edge[i].c) && edge[i].w) {
				dis[v] = dis[u] + edge[i].c;
				flow[v] = min(flow[u], 1ll * edge[i].w);
				pre[v] = i;
				if (!in_queue[v]) {
					in_queue[v] = true;
					q.push(v);
				}
			}
		}
	}
	return (dis[t] < inf);
}

void edmonds_karp(ll mid) {
	while (spfa()) {
		int cur = t;
		mf += flow[t];
		while (cur != s) {
			edge[pre[cur]].w -= flow[t];
			edge[pre[cur] ^ 1].w += flow[t];
			cur = edge[pre[cur] ^ 1].to;
		}
		sum += max(0ll, 1ll * (mid - dis[t] + 1ll) * flow[t]);
	}
}

bool check(ll mid) {
	cnt = 1;
	mc = mf = sum = 0;
	memset(head, 0, (t + 1) * sizeof(int));
	for (int i = 1; i <= m; i++) {
		add(ui[i], vi[i], wi[i], 1);
	}
	edmonds_karp(mid);
	return (sum >= k);
}

ll work() {
	ll l = 1, r = 1e12;
	while (l < r) {
		ll mid = (l + r) >> 1;
		if (check(mid)) {
			r = mid;
		} else {
			l = mid + 1;
		}
	}
	return l;
}

int main() {
	int u, v, w, c;
	while (scanf("%d%d%d", &n, &m, &k) != EOF) {
		s = 1, t = n;
		for (int i = 1; i <= m; i++) {
			scanf("%d%d%d", &ui[i], &vi[i], &wi[i]);
			ui[i]++, vi[i]++;
		}
		if (!k) {
			puts("0");
			continue;
		}
		ll ans = work();
		if (ans != 1e12) {
			printf("%d\n", ans);
		} else {
			puts("No solution");
		}
	}
	return 0;
}