【概括性记录/讲解】信息矩阵、Hessian矩阵、协方差的逆
在最大后验估计中 如果分布为高斯分布 信息矩阵 = 协方差的逆
多元变量x
x又两部分组成：
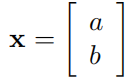
它的协方差矩阵为：
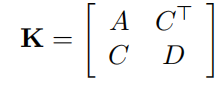
其中：
它的信息矩阵就是协方差矩阵的逆：
作用：便于计算边界概率和条件概率 但边际概率对于协方差矩阵的操作是很容易的，但不好操作信息矩阵。条件概率恰好相反，对于信息矩阵容易操作，不好操作协方差矩阵。
Hessian矩阵在最大似然问题中（MLE）约等于信息矩阵
直接反映到最小二乘的问题上：
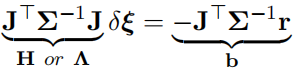
这里的 H 也被称为信息矩阵 个人理解这个信息矩阵和上一个信息矩阵虽然叫一个名 但是可以理解成两个东西
这里信息矩阵的作用：分析残差矩阵的稀疏性 进行下一步的计算 也可以用作滑动窗口算法的的分析
最大后验、最大似然、最小二乘
最大似然和最小二乘 同为求最优参数的方法 当分布为高斯分布时 二者形式上近似相同 但思想上完全不同
最小二乘：构建误差和 通过调整参数使得误差之和最小 当误差最小时认为获得了最优参数值
最大似然：前提是知道概率密度函数 求概率密度之和 通过调整参数得到最大概率 当得到最大概率时 即认为获得最优参数值
最大后验 即比最大似然多了一项先验
实际应用中大部分使用的为最大似然
