【矩阵基础与维度分析】【公式细节推导】矩阵非线性最小二乘法泰勒展开
1|0最小二乘法的一般形式
2|0将残差写成向量的形式

和上面的相比 每个计算的还是某一时刻的误差 将全部的误差求平方再求和 就相当于它的转置乘以它本身 即:
所以有如下等式
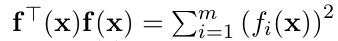
则它的雅克比矩阵为:
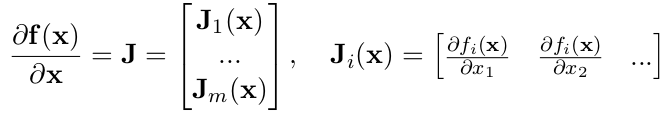
这里每个雅克比矩阵的维度都为
3|0最小二乘泰勒展开
单项展开

整体展开

上述步骤更具体一些
第一行后面到第二行推导:
这里进行一下维度分析:
f为某一时刻确定的误差值 所以是标量
J参照上面的那个J的维度分析:
为增加量 这里为列向量
所以可得以下结论:
- 为标量
- 为标量
- 为标量
所以有:
维度分析对于矩阵运算很重要
__EOF__
本文作者:铃灵狗的水墨书香
本文链接:https://www.cnblogs.com/linglingdog/p/15946532.html
关于博主:评论和私信会在第一时间回复。或者直接私信我。
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
声援博主:如果您觉得文章对您有帮助,可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力!
本文链接:https://www.cnblogs.com/linglingdog/p/15946532.html
关于博主:评论和私信会在第一时间回复。或者直接私信我。
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
声援博主:如果您觉得文章对您有帮助,可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力!

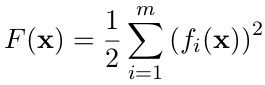


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】