IMU数学模型详细推导
旋转运动学
质量块在body坐标系下的坐标为：
body坐标系为imu坐标系 惯性系为世界坐标系
只考虑旋转 旋转到惯性系下：
对时间求导 如下：
其中
对\(R\)的求导 有如下推导：
其中\([w^b]_\times=w^{\wedge}\)
\([w^b]_\times r =w^b\times r\)
对坐标求二阶导 得出：
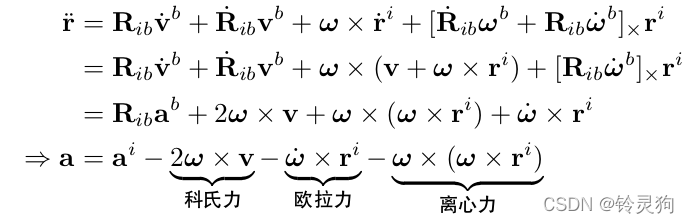
其中\(\dot{R}_{ib}w^b =R_{ib}[w^b]_\times w^b =R_{ib}w^b\times w^b =0\) 自身和自身的叉乘为零
imu测量模型
imu中包含两种测量模型：加速度计和陀螺仪
加速度计用来测量加速度的大小 陀螺仪用来测量角速度的大小
加速度计
这里用弹簧模型理解 实际中会使用电容器
加速度的坐标系通常为东北天坐标系：
静止时 加速度计测得加速度为0 重力加速度为g
自由落体时 加速度计测得加速度为g 重力加速度为0
加速度计不需要考虑科氏力的影响 因为在某一时刻科氏力会等于0 达到平衡状态
陀螺仪
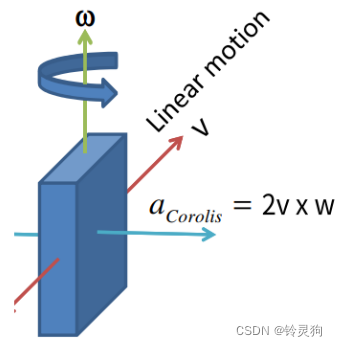
测量 a 和 v 可以求出 w
但是会受到科氏力的影响 所以会采用音叉陀螺 将科氏力抵消掉
误差模型
IMU误差分为确定性误差和随机误差
确定性误差
确定性误差主要分为：bias和scale
bias即经常说的零偏：理论上没有外力作用时 IMU的传感器输出应为0 但实际上会出现一个偏置bias
scale可以看成实际数据与传感器输出数据之间的一个比值
以及还有xyz轴不重合的误差
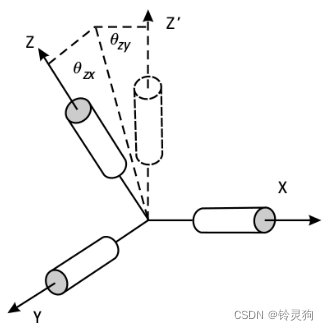
常使用六面法标定加速度计和陀螺仪 不过多介绍
随机误差（重点）
随机误差分为高斯白噪声和bias随机游走
连续时间上的随机误差
高斯白噪声：
狄拉克函数：当\(t_1 = t_2\)时为1 其他时刻均为0 说明了每段时间的独立性
bias随机游走：
我们认为它的导数为高斯白噪声 \(w\)为方差为1均值为0的白噪声
离散时间上的随机误差
一个单轴角速度受到高斯白噪声和bias的影响：
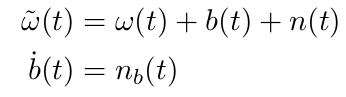
当传感器采集信号时 认为采样时间段内信息为常数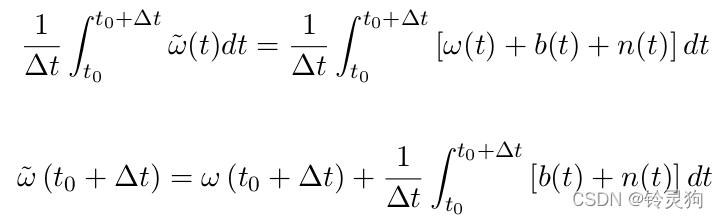
我们无法确定随机误差的积分是否为常数 所以单独对这两种随机误差进行分别积分：
高斯白噪声：
高斯白噪声的方差（这里为什么要平方？ 因为这就是方差的定义 详见《矩阵分析与应用》）
我们认为：
其中：
可以得出结论：对比高斯白噪声的连续时间和离散时间的\(n_d[k]\)，高斯白噪声的连续时间和离散时间相差一个\(\frac{1}{\sqrt{\Delta t}} \quad\) 其中\(\Delta t\)为传感器的采集时间（1/HZ）
bias随机游走：
bias积分部分：
协方差为：
上面都不重要
结果：
其中：
得出结论：同样这里对比的是\(b_d[k]\) bias随机游走的噪声方差从连续时间到离散时间需要乘以一个\(\sqrt{\Delta t}\)
实际操作时 我们会使用kalibr_allan对imu进行标定 算出高斯白噪声误差和bias随机游走误差（即\(\sigma\)）
使用ROS 生成imu数据包 再使用kalibr_allan将数据包转换为mat文件 再输入进kalibr_allan
IMU模型
其中b为bias随机游走误差 n为高斯白噪声
\(w^b\)为理想值 \(\tilde{w}^b\)为测量值 a同理
运动模型的离散积分
欧拉法
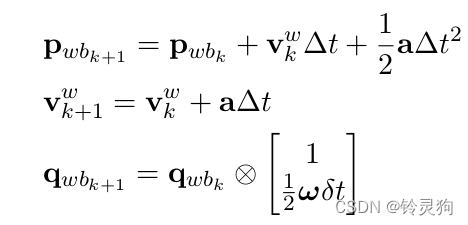
其中
对应到代码：
//delta_q = [1 , 1/2 * thetax , 1/2 * theta_y, 1/2 * theta_z]
Eigen::Quaterniond dq;
Eigen::Vector3d dtheta_half = imupose.imu_gyro * dt /2.0;
dq.w() = 1;
dq.x() = dtheta_half.x();
dq.y() = dtheta_half.y();
dq.z() = dtheta_half.z();
dq.normalize();
/// imu 动力学模型 欧拉积分
Eigen::Vector3d acc_w = Qwb * (imupose.imu_acc) + gw; // aw = Rwb * ( acc_body - acc_bias ) + gw
Qwb = Qwb * dq;
Pwb = Pwb + Vw * dt + 0.5 * dt * dt * acc_w;
Vw = Vw + acc_w * dt;
中值法
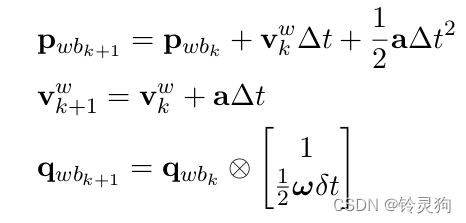
其中
对应到代码：
//delta_q = [1 , 1/2 * thetax , 1/2 * theta_y, 1/2 * theta_z]
Eigen::Quaterniond dq;
Eigen::Vector3d dtheta_half = (imupose.imu_gyro + imudata[i - 1].imu_gyro)/2.0 * dt /2.0;
dq.w() = 1;
dq.x() = dtheta_half.x();
dq.y() = dtheta_half.y();
dq.z() = dtheta_half.z();
dq.normalize();
/// 中值积分
Eigen::Vector3d acc_w = (Qwb * dq * imupose.imu_acc + gw + Qwb * imudata[i - 1].imu_acc + gw)/2.0;
Qwb = Qwb * dq;
Pwb = Pwb + Vw * dt + 0.5 * dt * dt * acc_w;
Vw = Vw + acc_w * dt;
