2024年8月4日 加训

2024年8月4日 加训

A

$$\lvert S\cap T\rvert \in V_{f(T)}$$

对于一个 $T$，限制形如 $T$ 中的元素有 $V_{f(T)}$ 个，求 $T$ 的大小为各种的子集，并将其设置为不合法

$g(S)$ 集合 $S$ 是否合法

规约不来。不会

正解

枚举 $S$，然后相应地规约限制

B

看起来像支配一类的问题.不是交换相邻

没思路，什么牛魔题

正解

确实是支配，你需要观察到交换 $A, B$，交换 $B, C$ 相当于可以交换 $C, D$。

于是需要交换的得形成一个连通块，你进一步考虑怎么搞最小生成树之类的

C

只有一个合法 $m$

若 $k = 1$，$m = n\times \max$，这个时候至少要 $n$ 次询问得到 $\max$

$m$ 是 $\max$ 的倍数，考虑找出 $\max$，这题只需要找到 $m$，所以只需判断是否有一个合法 $m$

花费 $n - 1$ 次找到 $\max$。

然后询问 $n$ 次 $k\max$，假设 $k_1$ 得到 $r_1$，$k_2$ 得到 $r_2$。

整个序列的最大和为 $n \times \max$，显然答案小于 $n/k \times \max$。

对 $n / k$ 种答案分别查询 $k$ 次即可

why? WA? 查询的时候没判断询问是否合法

D

首先得到若干连通块，和桥

首先一定要连接成连通块，所以建桥的费用是 $c\times (components - 1)$

components 内部的桥，考虑分成左右两部分，考虑分配成尽量相等的两份，这玩意应该很 NP，只能背包

于是考虑怎么快速背包，背包复杂度都爆炸了。不会，下一题

这题 $m$ 搞这么大干锤子

正解

草，直接背包 $n^2/\omega$ 居然可以过。

E

本质不同的子串数量

如何区分，保证任意两个都不同

如果有相同的两对组合，显然寄了，无法区分

如果没有，显然直接结束游戏，因为你自己建个sam出来就好了，时间复杂度 $O(len * n) = O(27000) = O(1)$。

先搞个 X，还得区分前后。来个 XO？

这怎么做，本质不同子串有什么很好的做法吗？我只会在 SAM 上统计啊哥们

难道说，对于 0/1 串，只要翻转不同，本质不同子串数量就不同

010

0, 1, 01, 10, 010

110

0, 1, 10, 11, 110

对字符串长度限制比较松

对于第 $i$ 个串，随机是不是对的？

笑死，直接随机过了

s[i].push_back((rng() % 8) ? (i & 1 ? 'X' : 'O') : (i & 1 ? 'O' : 'X'));

生成器如上，考虑在字符串中插入一些连续段，这样比较好区分你是第几个串，因为连续的多了，本质不同的就少了，这样长度带来的影响比较大，所以能区分。

此外，对奇偶分类连续段的字符是 X 或 O，这样能长度相差为 30 的串基本不可能判断不出来

建议赛后看正解

正解

这题正解就是随机，Hard Version 是构造 XOXXX... 的串，理由是这玩意不重复，能区分前后，并且好计算本质不同子串数目。

F

给出一个双射函数，求反函数

给出一个函数值，求点

初始括号序列合法，最终也合法

不会

正解

先考虑括号树上的权值，如下图：

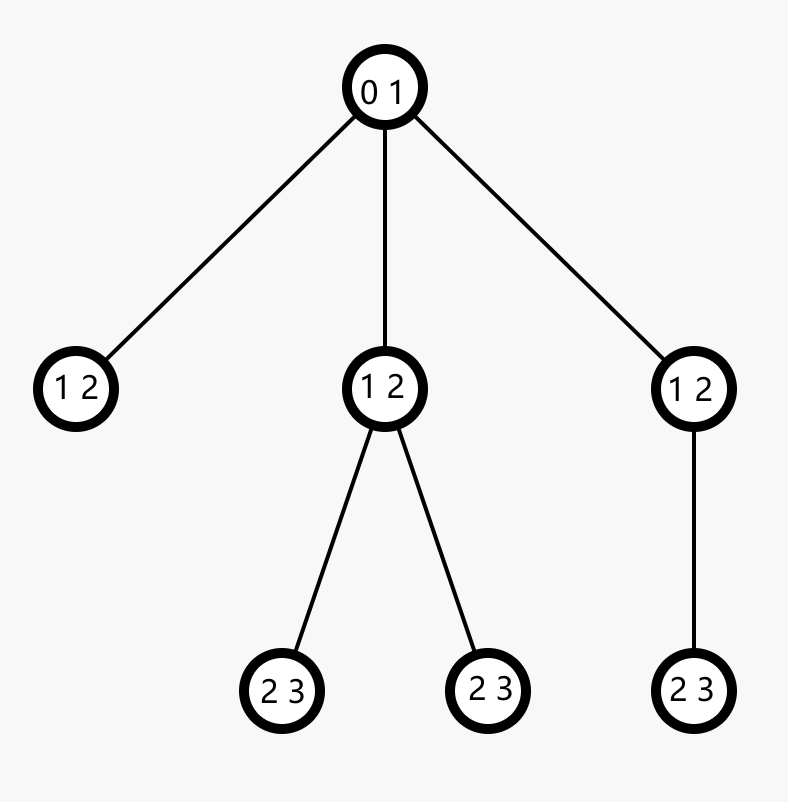
注意儿子是从左到右的顺序的。

于是这会生成一个括号序列，并且我们知道其对应的权值：

()((()()(())))
01111222222333

考虑怎么通过上面这个括号序列，确定下面的数字。

首先起始的是 $0$，接下来一定都大于等于 $0$，当出现右括号时，其匹配的一定是最先出现的左括号，并且权值是左括号权值 $+1$，故可通过如下流程确定：

int cur = 0;
queue<int> Q;
for (int i = 0; i < n; ++i) {
	char ch = s[i];
    if (ch == '(') {
        val[i] = cur;
        Q.emplace(cur);
    } else {
        val[i] = Q.front() + 1;
        Q.pop();
    }
    cur = val[i];
}

接下来考虑如何利用上面的两个信息还原树。我们知道，每一个左括号都代表了一个节点，其儿子的左括号一定出现在这个点的右括号之后，出现在其兄弟的右括号之前。此外，同样的，权值为 $v$ 的右括号匹配的是第一个未被匹配且权值为 $v-1$ 的左括号。

流程如下：

queue<int> Q[max_val];
vector<int> son(n);
int tot = 0, fa = 0;
for (int i = 0; i < n; ++i) {
    char ch = s[i];
    int v = val[i];
    if (ch == '(') {
        int x = ++tot;	// 当前节点的编号
        fat[x] = fa;
        son[fa].push_back(x);
        Q[v].emplace(x);
    } else {
        fa = Q[v - 1].front();	// 当前节点作为父亲
        Q[v - 1].pop();
    }
}
for (int i = 0; i <= tot; ++i) reverse(begin(son[i]), end(son[i]));	// 真实情况是倒序