PageRank与社交网络模型评估
SNS社交网络在近几年流行起来,并呈现出火爆的增长趋势。在仿制国外Facebook、twitter等成功先例的基础上,国内的人人网、新浪微博等一系列社交网络正风生水起。
这些社交网站表面上看起来十分普通和其他网站别无二致,但我们可以研究它们背后更深层次的数学原理,从而更有利于推广营销。在后面的分析中,我会分别举例,大家就会明白实际中的应用价值。
我们需要考虑的是怎样度量一个网络。网络其实就是一张图,图中有各个节点,节点连接起来,形成边。在社交网络中,每个人就是一个节点,人们通过好友关系相互连接。节点是有权重的,就像人具有影响力一样。

给你一张网络拓扑图,你怎样挖掘这张图所蕴含的信息呢?你怎样知道图中哪一个节点是最重要的?事实上有很多方法,我们自己也可以定义度量的标准。经常用到的有Degree Centrality,Eigenvector Centrality,Katz Centrality,PageRank,Closeness Centrality,Betweenness Centrality,Transitivity……它们从简单到复杂,从偏重某个属性到综合考虑,很多都在现实中合理地使用着,例如PageRank就是Google使用的网页排名方法。
1. Degree Centrality(节点度)
这是对网络最为简单直白的一种度量:仅仅统计每个节点有多少边。它的现实意义在于有更多边的节点具有更大的连接性,就像有更多好友的人具有更大的影响力。 例如对一个产品做推广营销,我们发放免费的试用样品给消费者,如果消费者满意他们就会购买,并且推荐给自己的朋友也去购买。这就是口碑影响力。作为厂家, 我们当然希望将样品发放给更具影响力的人,因为他们的一句赞美会传递到更多的节点上,为我们带来更多的潜在客户。我们知道,图分为有向图和无向图,他们的 区别在于节点之间的联系是否是双向的。例如Facebook或者人人网中的好友关系,就是一个无向图,你是我的好友那么我也是你的好友;而twitter 或者新浪微博则是一个有向图,因为我“关注”(follow)某些人,又有另外一些人“关注”我,这是一个从一个节点指向另一个节点的关系,不具有可逆 性。我们在讨论Degree Centrality时,对于有向图来说,其实有in-degree centrality和out-degree centrality两种。例如在微博上很多人关注了李开复,也就是说有很多节点指向他,那么李开复就具有很高的in-degree centrality. 但是要小心,in-degree高的节点不一定是最有价值的,例如在论文参考文献引用中,一篇文章的in-degree很高表示很多人引用了这篇论文。这 篇文章可能提出了一个有价值的研究问题,但是却犯了明显的错误,于是大家在写这个研究方向的论文时都会说:“快去围观这篇文章,作者太SB了,哈哈哈 哈……”
我们希望通过Degree Centrality来找出最有影响力的节点们。问题来了,想要获得具有Degree Centrality最高的前10个节点,我们需要知道整张图的结构才行。从数学上讲,即需要得到图的邻接矩阵A,对于A中的每一行统计有多少个1,最后进行排序取前k个即可得到Degree Centrality值最高的前k个节点。这在实际中并不可行,你并不是Facebook的所有者或者人人网的管理员,你怎么知道整个社会网络里谁的好友更多?
2. Eigenvector Centrality(特征向量)
这是对Degree Centrality的一种改进版。我们希望得到节点重要性的估值,但什么是重要性?什么是影响力?在Degree Centrality中,所有的邻居节点都是平等的。而在实际情况中,不同的邻居节点可能会有不同的价值。例如我有10个好友,他们都是普通人,而如果有一个人他也有10个好友,但是他的好友都是李嘉诚巴菲特奥巴马们,显然,我比不上他,自惭形秽了。
为此我们建立另一种模型:给邻居节点打分,高分的邻居会给予我更多积极的影响,使得我的得分也升高。设xi(t)为节点i在t时刻的centrality评估值(得分),centrality值越高说明这个节点越重要。则
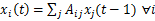
(1)
或者表示为矩阵形式
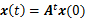
(2)
其中A为图的邻接矩阵。不知道邻接矩阵?回去复习线性代数离散数学和数据结构吧……
公式(1)比较好理解。基本思想其实就是说,节点j为节点i的邻居节点(我所说的邻居意思就是他们有边相连),在t-1时刻,我们对j叠加求和,意思就是 统计节点i的所有邻居节点的centrality值,然后累加,就是t时刻节点i的centrality值。这个公式对所有节点有效,如果我的邻居们的 centrality值改变了,我的值也会改变,所以这是一个不断迭代的过程,直到最后所有节点的值在一个阈值内进行可忽略的波动,即收敛。
第二个公式x(0)是0时刻初始化时所有节点的centrality值,它是一个数组。而
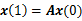
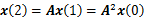
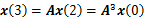
不断迭代就可以得到公式(2)了。
于是x(0)可以看作是A的特征向量Vi的线性组合,我们可以选取合适的ci使得等式
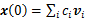
(3)
成立。
结合(2)(3)两个式子,我们得到
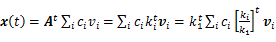
(4)
其中ki为矩阵A的特征值,k1为特征值中的最大值。
当k>1时,
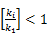
,于是当
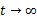
时,
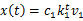
,或者直接表示为
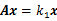
(5)
这就是eigenvector centrality。我们如果得到图A的邻接矩阵的特征向量,那么这个向量x就是所有节点的eigenvector centrality值。我们只需解方程(5)即可。它的一个明显的属性就是,xi即节点i的eigenvector centrality,与该节点所有邻居的eigenvector centrality之和成正比。即
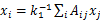
(6)
所以,这正解决了我们之前的问题,它将我们邻居的重要性施加到我们自己身上。有几种情况会使得xi的值很大,一是节点有很多邻居,二是它有一个重要邻居(该邻居拥有高eigenvector centrality值),或者以上两种情况同时存在。
同样的问题在这里也存在,那就是我们必须知道图的邻接矩阵,也就是整个网络的拓扑结构。如果网络中有100万个节点,我们生成一个100万×100万的矩阵也是困难的。另外,还有可能出现下面的情况
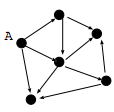
这是一个有向图,注意节点A,它没有in-degree,也就是说没有其他节点可以影响到它的centrality值。假如A的centrality值是 0,那么它对它的3个邻居的贡献也为0,其中最上面的那个邻居只有A对它施加影响,于是它的centrality值也为0,最后我们一步步地推断,会发现 整个图所有节点的centrality值都是0,也就是说图的邻接矩阵A=0.这不是我们预想的那样,因为如果我们希望对网页做PageRank,这将导 致所有页面的PageRank值都一样,没法做排名了。
上边提到两种网络模型,都有着这样那样的缺陷。下面我们继续来改善建模。
3. Katz Centrality
Katz Centrality解决了之前的问题。它的原理与eigenvector centrality差不多,只是我们给每一个节点提供一个初始化的centrality值β,即对式(6)做简单改变:
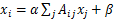
(7)
α 和 β 都是正常数。
使用矩阵表达式,我们得到:
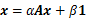
(8)
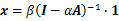
(9)
我们只关心centrality值的相对性,也就是说不管你的centrality值是10还是100,我们只关注你的centrality值是不是大于 我的centrality值,因为我们希望找到centrality值最大的前10个节点,目的是做排名。于是β可以设置为1,于是Katz Centrality表达为:
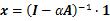
(10)
事实上α和β的比值体现了对邻居节点centrality值的侧重,如果α=0那么所有的节点的centrality值都是β=1了,完全不受邻居的影响了。所以说这个公式更具有普遍性,这就是数学之美。
需要注意的是α不可以太大,当
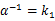
会导致
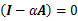
,于是
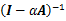
无法收敛。所以有
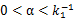
.
要计算Katz centrality,就要做逆矩阵运算 ,直接计算的复杂度为O(n3)。我们可以用迭代法
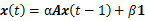
(11)
4. PageRank
Katz centrality的一个缺陷就是,一个拥有高centrality值的节点会将它的高影响力传递给它的所有邻居,这在实际生活中可能并不恰当。比如说 Google的网页有很高的centrality值,同时Google也链接了海量的页面。如果Google的网页链接到了我的网页,那我的网页作为一个 无名小卒centrality值岂不是有可能比Google还高?我们希望Katz centrality能够由节点的out-degree稀释,或者说我的centrality值能平均分给我的邻居,而不是给每个邻居都得到我的整个 centrality值。用数学语言表达为
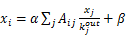
(12)
对比公式(7)就很容易理解这里对Katz centrality做的修改了。
对于没有外链的节点(例如很多链接指向了一张图片,但图片是没有out-degree指向别处的),将其
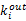
值设为1.我们将式(12)写为矩阵形式:
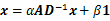
(13)
其中D是对角矩阵,
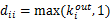
.同样设β=1,上式可以变形为
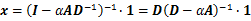
(14)
这就是著名的PageRank算法。
同样,α的取值也是有范围的,它应该小于AD-1最大的特征值的倒数。对于无向图来说,这个值是1,对于有向图来说就不一定了。Google的搜索引擎将α设为0.85。同样,要执行这个算法,我们需要知道整个图的拓扑结构。
5. HITS算法
与PageRank算法类似,HITS也是在网络建模和权重排名中比较经典的算法。
有的时候我们希望把高centrality值赋予那些链接了很多重要节点的节点,例如综述性的学术论文引用了该研究领域内的大量重要论文,于是这篇综述也 被认为很有价值。因为即使这篇论文没有为该科研领域做出什么突破,但它总结了已有成果,告诉大家去哪里找做出了突出贡献的论文。
于是我们拥有两种节点:authorities(权威型)的节点包含了具有贡献的原创信息,hubs(枢纽型)节点总结了很多信息,指向了很多 authorities节点。Kleinberg是康奈尔大学一位十分牛B的年轻教授(70后年轻有为啊!),他提出了hyperlink- induced topic search (HITS)算法来量化计算authority centrality和hubs centrality。
在HITS中对于某个节点i,xi用来表示authority centrality,yi用来表示hubs centrality。每个节点既有authority属性又有hubs属性。节点若有高xi值则该节点被很多其他hub节点关注,如论文被大量引用、微 博有很多粉丝。节点若有高yi值则该节点指向了很多其他authority节点,例如一篇综述论文,又例如hao123.com这样的网址导航站点(理解 百度为什么要收购hao123了吧)。
用数学语言描述如下:
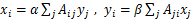
(15)
或者矩阵表达式
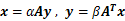
(16)
合并演化得到
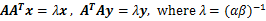
(17)
这意味着authority centrality为AAT的特征向量,而hubs centrality为ATA的特征向量。有趣的是AAT和ATA拥有相同的特征值λ,大家可以自行证明。
继续演化,我们对式(17)左乘一个AT,得到
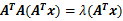
,也就是说
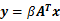
(18)
我们知道了x,也就可以计算得到y。
6. 社交网络建模工具(Python)
最近比较忙,如果没有需求,这个系列可能就不会再继续写下去了。下面用一个python程序来演示社交网络的建模分析,以实际应用作为结束吧。
假设有这样两个文本文件sigcomm_author.txt和sigcomm_network.txt,文件内容如下:
sigcomm_network.txt:
1,2 (ID_1 与 ID_2 有合作发表论文)
3,4 (ID_3 与 ID_4 有合作发表论文)
4, 216 (ID_4 与ID_216 有合作发表论文)
…
sigcomm_author.txt:
1: Amer El Abbadi (ID_1: name)
2: Thomas Lui (ID_2: name)
…
这是一个学术圈的社交网络,描述了发表论文的作者之间的一些合作关系。它一个无向图,也就是说[ID_1, ID_2] 等同于 [ID_2, ID_1]。通过编写程序,我们可以挖掘如下信息:
- n: 节点数量(有多少个作者)
- m: 边的数量(有多少个论文合作关系)
- 网络中连接部的大小(节点互相连接形成网络连接部,另外还可能有孤立的一些节点)
- clustering coefficient群聚系数
- 网络直径(两两节点间会有一条最短路径,在所有的节点对中,最长的最短路径有多长)
- 节点度分布
- 最短路径长度分布
- degree centrality
- eigenvector centrality
NetworkX是一个用Python语言开发的图论与复杂网络建模工具,内置了常用的图与复杂网络分析算法,包括我已经介绍过的degree centrality,eigenvector centrality等等。使用NetworkX可以方便的进行复杂网络数据分析、仿真建模等工作。
一般Linux都默认自带Python运行环境,Ubuntu下只需要执行以下命令即可获得NetworkX库进行程序开发。
Windows下则需要手动安装,具体可以参考这个安装步骤。环境都搭建好了之后就可以对社交网络之间的关系进行分析了,查看这个入门指南。
回到上文提出的例子,在调用NetworkX提供的接口的基础上,我们可以挖掘论文作者之间的关系,分析整个网络的一些属性。示例源代码和测试数据下载。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号