【论文阅读】Feature Inference Attack on Model Predictions in Vertical Federated Learning

发布在ICDE2021的一篇文章，链接：Feature Inference Attack on Model Predictions in Vertical Federated Learning

相关阅读：联邦学习安全么？（数据攻击）

本篇文章名为纵向联邦预测模型的特征推理攻击，本文贡献为：

 

 

 

在我们通常的纵向联邦学习中，把多方相互之间的特征值通过一些各自的处理，在相互之间传一些参数来实现共同模型的训练。训练的数据一般都是有监督学习的数据，也就是能够有标签值的数据。

其中拥有标签值的一方为主动方，其余没有标签值的一方或者几方为被动方。

在本篇文章中，把拥有标签值的一方看作进攻方，而没有标签值的一方或者几方所拥有的特征值看作目标值，进攻方通过一定的方法得到目标方的目标值，也就是通常模型中被动方的隐私数据。

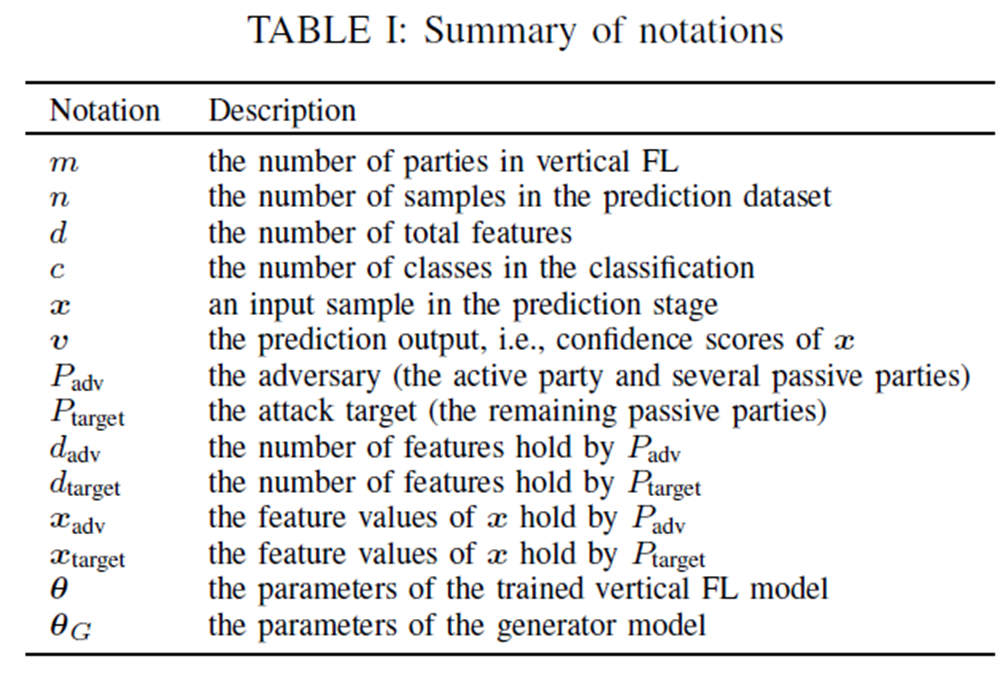
首先我们看第一个，解决逻辑回归的等式求解攻击，多分类比二分类简单，所以这里仅仅对多分类逻辑回归做解释。

 

 

 上图4式和5式是我们用逻辑回归解决多分类问题的通用的公式，其中作者在4式中把x和θ分成了攻方和目标方的数据。

本文作者将5式双方取对数，并对两个相邻类别概率v的对数取差值以得到无关z值的一个等式：等式8。其中a‘k是一个c-1维向量，其实就是限制等式8为c-1个方程。

但是在后面推理的时候本文有一些为了逻辑上方便而把纵向联邦限制减少的做法：把目标方或者说被动方的参数θ看作进攻方或者主动方能够得到的数据。

实际情况中，主动方或者进攻方在一般的纵向联邦框架中是无法得到被动方的参数θ数据的。

本文中我们姑且认为进攻方能得到，那么等式8中的未知数只有xtarget了，而xtarget的维数为dtarget，数量为目标方所用拥有的特征数。

这里我们把xtarget的未知数看作自变量，个数为目标放所拥有的特征数。那么也就是说，dtarget个自变量，c-1个方程，当dtarget≤c-1的时候，方程必有解。

这就是文章所说的，等式求解攻击。

其次，我们看一下解决决策树模型的路径限制攻击。

 

 

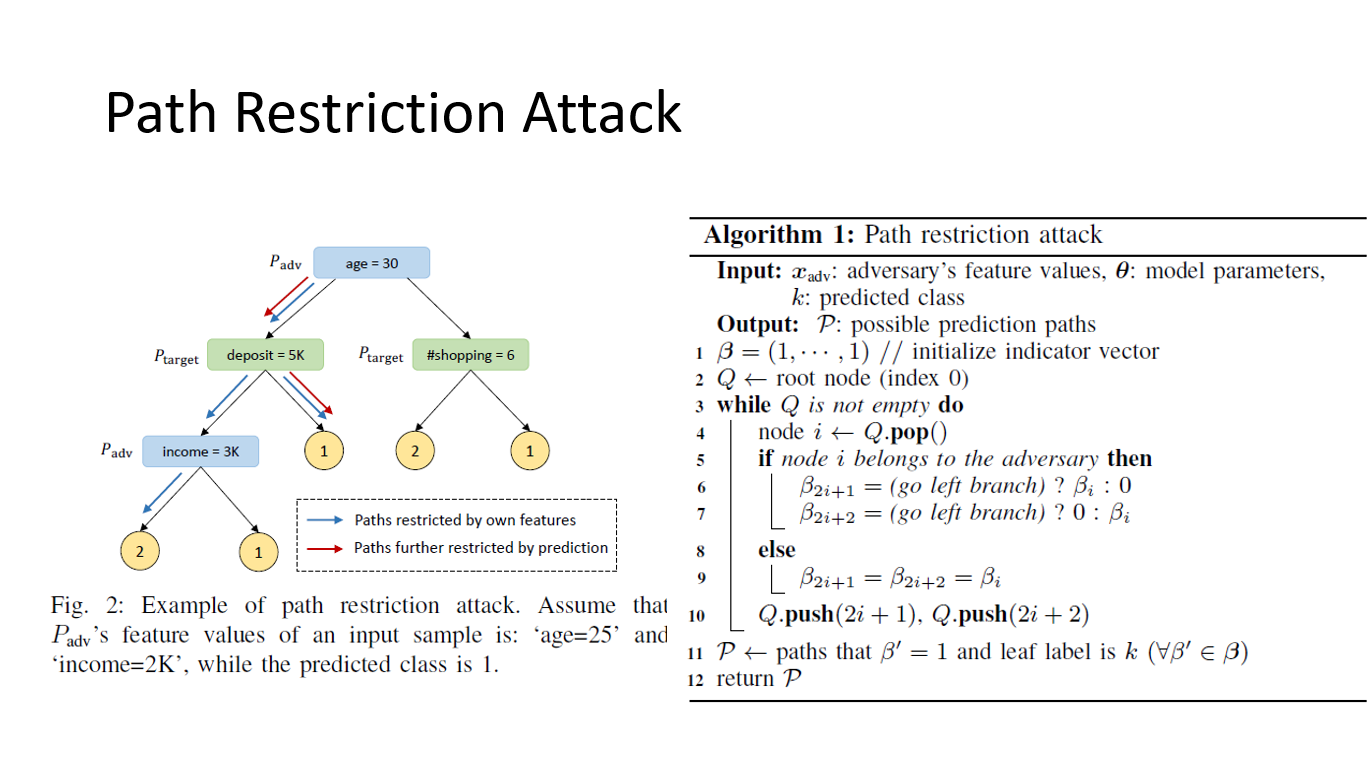
 这一部分看得也是有一点不明所以，因为文章似乎是把被动方用于分裂节点的特征也对主动方可见了，而一般的纵向联邦框架内是不可见的。比如FATE框架：

主动方可见的内容：

 

被动方可见的内容：

 

 

 

 

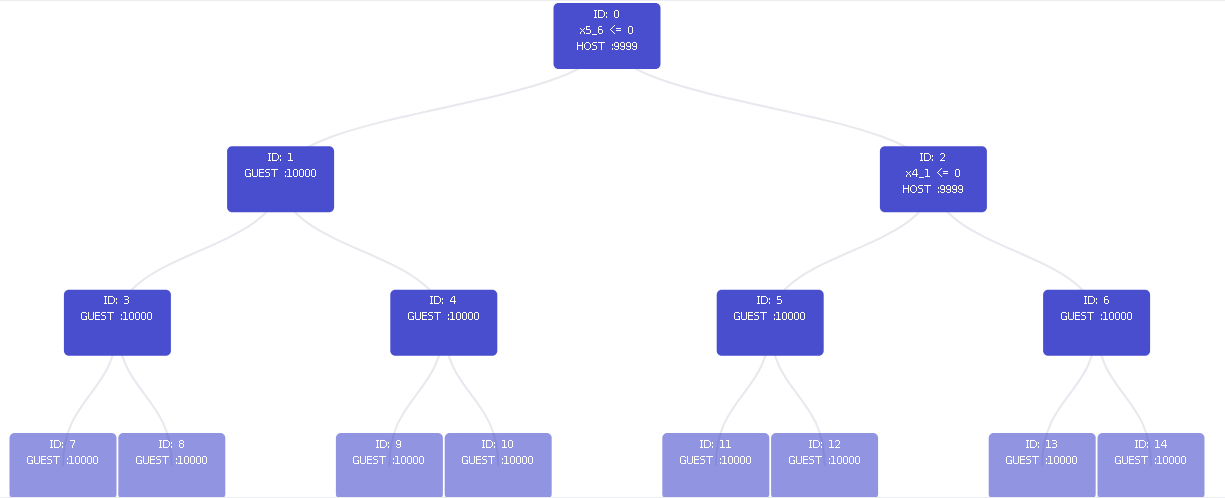
 在这里我们也姑且认为，标签内容对于主动方是可见的，那么主动方可以用自己所掌握的数据判断节点分支的与否进而得到被动方的节点特征的特征值或者范围。

右边代码就是指取得节点和路径的代码。

然后我们看本篇论文的重点，生成回归网络攻击。

 

 

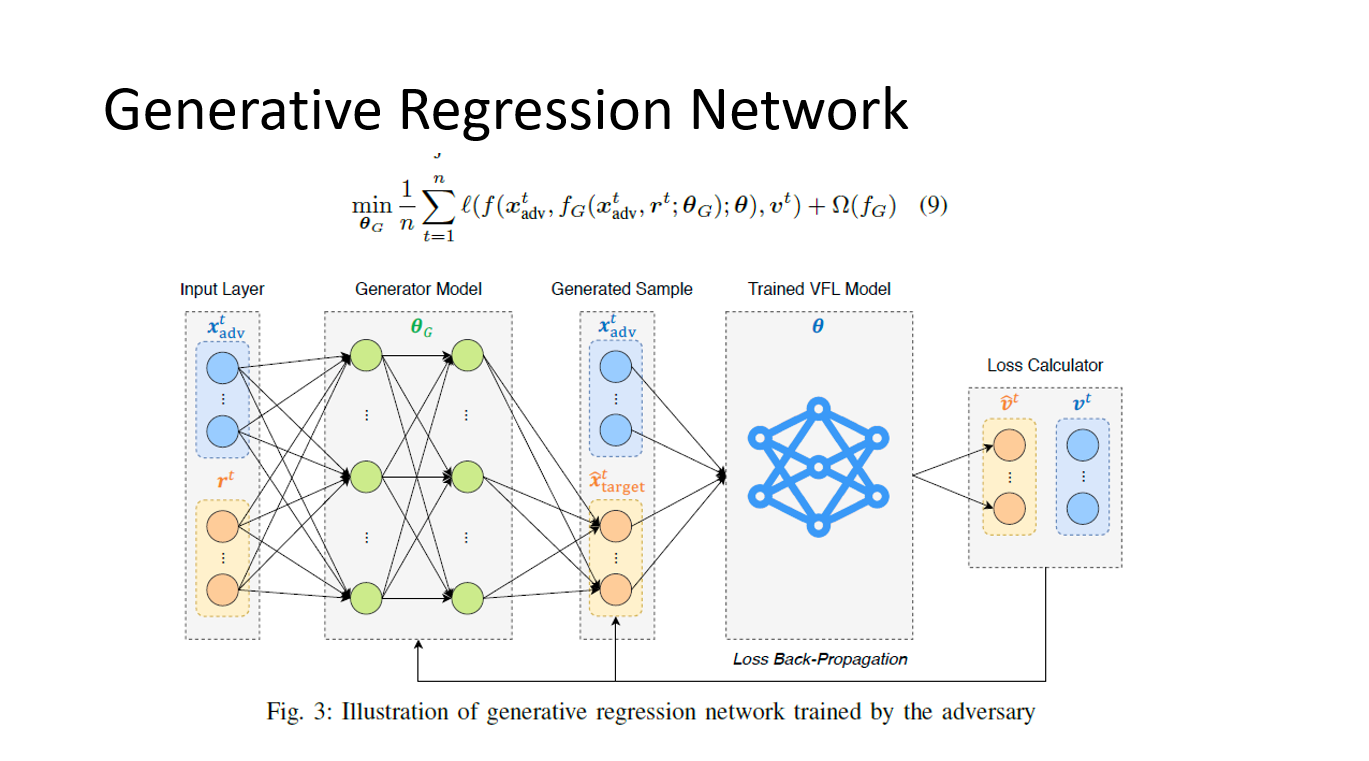
1、把进攻方所拥有的数据（蓝色）和随机生成的数据（橙色），合成一个d维向量，其中d为进攻方的特征数量和目标方特征数量之和，随机生成的数据是为了初始化生成模型的初始输入。

2、生成模型计算之后，输出生成模型对于目标方特征值的预测。

3、把生成模型生成的目标放特征值的预测（橙色）与进攻方所拥有的数据（蓝色）合并，得到另一个d维的向量，作为已经生成的纵向联邦学习预测模型（比如神经网络）的输入。

4、得到输出的对不同类别的预测概率矩阵（橙色），与真实的攻方特征值和目标方特征值得到的不同类别的预测概率矩阵（蓝色）求损失。

5、对得到的损失进行反向传播，修改生成模型的参数，得到新的生成模型对目标放特征值的预测。

这样的一种方法，对于目标函数为可微的情况下效果不错，也就说明可以用来对逻辑回归和神经网络进行生成模型攻击。

 

 

 最后是对随机森林的生成模型思想的攻击。

 

 

 

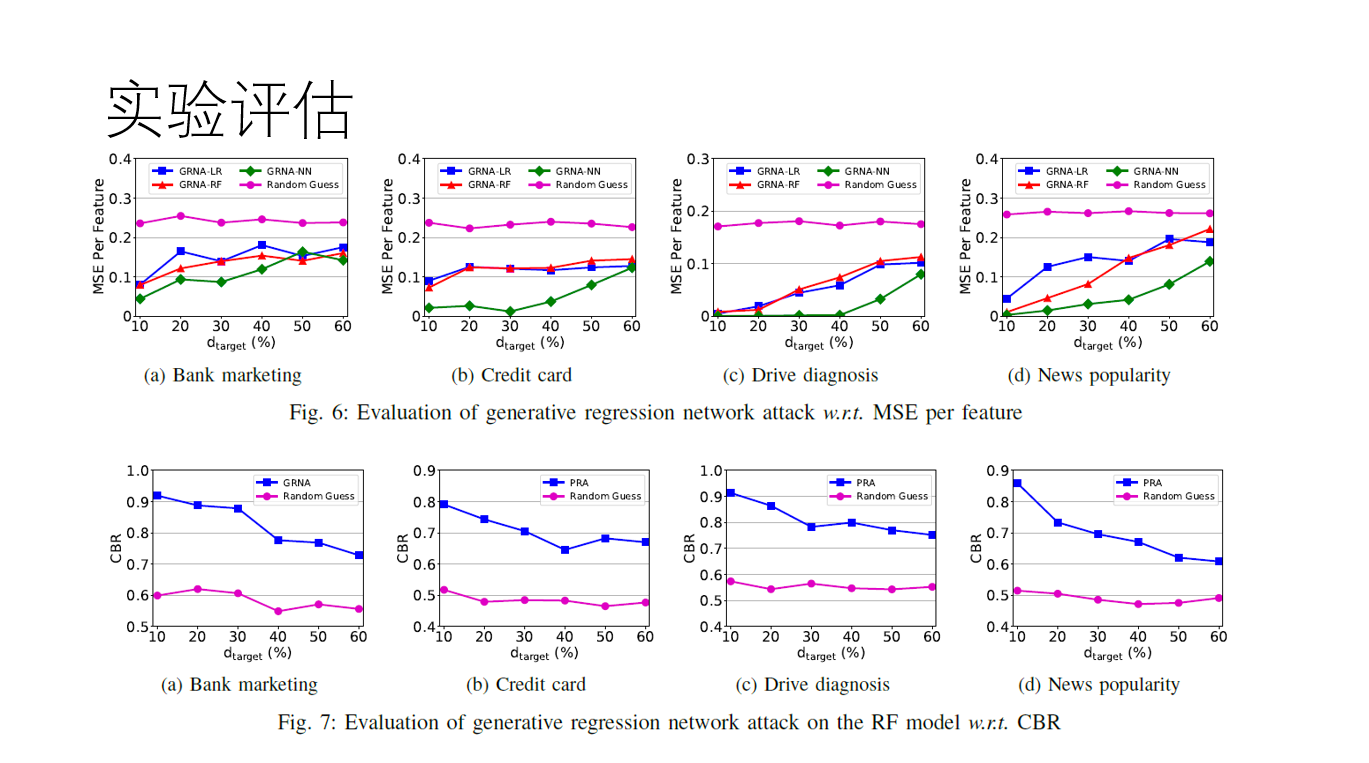
实验部分：四个数据集，分别是银行营销（20个特征的2分类），信用卡（23个特征的2分类），诊断（48个特征的11分类）和新闻流行（59个特征的5分类）。

 

 

 图中横轴表示dtarget所占的比例，比如当其是10%的时候，攻方和目标方所拥有的特征数分别是18个、2个；21个，2个；43个，5个；53个，6个。这个时候当然等式求解和路径限制攻击有很好的效果，比如等式求解的时候MSE很小，而路径限制的时候正确分支率很高。而且还有一个明显的趋势，即攻方所掌握的特征数越少，供给的准确率越低。其次就是第三个诊断数据集的一些奇怪表现，在MSE一直那么低的原因在于其类别为11个，特征数为48，在等式求解的时候更有优势，CBR一直那么高的原因在于其类别有11个，分支的信息会相对于二分类更多。