数理统计与数据分析-hw3
第八章
利用原始数据复现图8.3
illinois60=importdata('illinois60.txt');%载入伊利诺伊州1960年降雨量数据 illinois61=importdata('illinois61.txt');%载入伊利诺伊州1961年降雨量数据 illinois62=importdata('illinois62.txt');%载入伊利诺伊州1962年降雨量数据 illinois63=importdata('illinois63.txt');%载入伊利诺伊州1963年降雨量数据 illinois64=importdata('illinois64.txt');%载入伊利诺伊州1964年降雨量数据 illinois=[illinois60;illinois61;illinois62;illinois63;illinois64];%把五年的降雨量数据合成一个数据数组 x_=mean(illinois);%计算五年数据的均值 v_=var(illinois,1);%计算五年数据的均方差 lambda_1=x_/v_;%计算矩估计得到的lambda的估计值 alpha_1=x_^2/v_;%计算矩估计得到的alpha的估计值 lambda_2=1.96;%书上给出最大似然估计的lambda的估计值 alpha_2=0.441;%书上给出最大似然估计的alpha的估计值 x=0:0.01:2.5; y1=45.4*gampdf(x,alpha_1,lambda_1);%画出修正后的gamma函数的矩估计近似 y2=45.4*gampdf(x,alpha_2,lambda_2);%画出修正后的gamma函数的最大似然近似 figure histogram(illinois,11)%画出直方图 hold on plot(x,y1,'--',x,y2,'-')%画出曲线
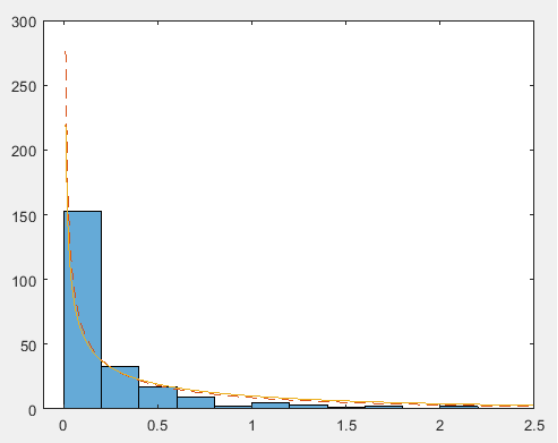
利用自主法复现8.4,并计算alpha和lambda的估计值的变异程度
M=1000;%进行1000次抽样 n=227;%抽取容量为227的样本 a=0.375;%设置矩估计的gamma函数的初始值 b=1.674;%设置矩估计的gamma函数的初始值 a0=[];%定义空数组 b0=[];%定义空数组 for i=1:M%开始循环 data=gamrnd(a,b,n,1);%随机抽取n个样本 x_=mean(data);%取n个样本的均值 v_=var(data,1);%取n个样本的方差 a1=x_^2/v_;%根据书中的对形状参数的估计公式得出a1 b1=v_/x_;%书中lambda的估计是尺度参数的倒数,也就是逆尺度参数(https://baike.baidu.com/item/伽马分布/7245468?fr=aladdin) a0=[a0 a1];%把循环得到的a1放入a0数组 b0=[b0 b1];%把循环得到的b1放入b0数组 end figure histogram(a0,10)%对a的抽样分布进行画图 figure histogram(b0,10)%对b的抽样分布进行画图 s_a=std(a0,1) s_b=std(b0,1)
Alpha的抽样分布:

Lambda的抽样分布:
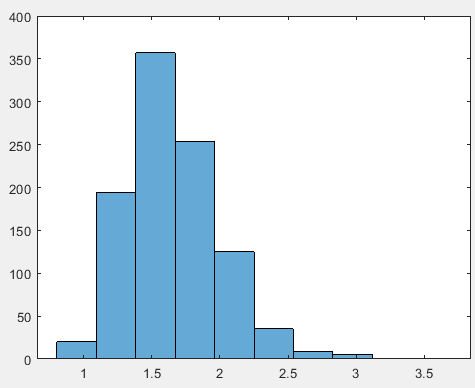
alpha和lambda的估计值的变异程度:
s_a =
0.0645
s_b =
0.3400
P218-7(a)(b)
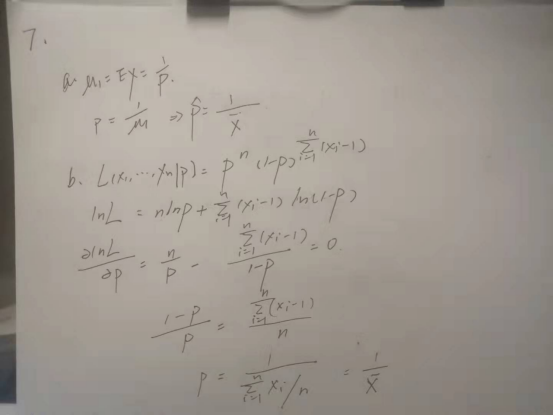
P220-20
M=1000;%进行1000次抽样 a=0;%原始的均值为0 b=10;%原始的标准差为10 mu0=[];%定义空数组mu0 sigma0=[];%定义空数组sigma0 for i=1:1000%开始循环 data=normrnd(a,b,100,1);%生成随机数,每组100个 [mu sigma]=normfit(data);%normfit得到这些数的mu和sigma mu0=[mu0 mu];%把前面得到的数据放入mu0数组 sigma0=[sigma0 sigma];%把前面得到的数据放入sigma0数组 end figure histogram(mu0,10)%对mu的抽样分布进行画图 figure histogram(sigma0,10)%对sigma的抽样分布进行画图 s_a=std(mu0,1) s_b=std(sigma0,1)
均值的抽样分布:

标准差的抽样分布:
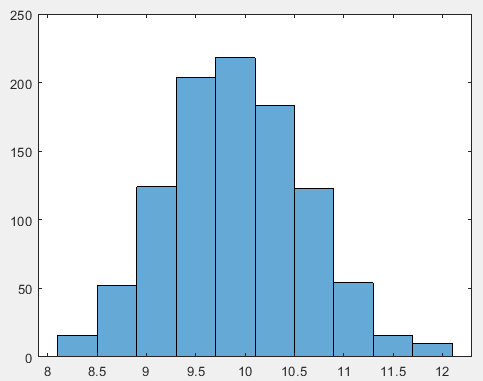
均值和标准差的估计值的变异程度:
s_a =
1.0470
s_b =
0.7003
P222-43
ga=importdata('gamma-arrivals.txt');%载入gamma-arrivals数据 x_=mean(ga);%计算gamma-arrivals的均值 v_=var(ga,1);%计算gamma-arrivals的方差 a=x_^2/v_%估计gamma分布的形状参数 b=v_/x_%估计gamma分布的逆比例参数 x=0:1:700; y=gampdf(x,a,b);%得出密度分布y figure histogram(ga,'Normalization','pdf')%画出比例密度分布直方图 hold on plot(x,y,'-')%画出矩估计得到的gamma分布 dfittool%在拟合工具箱里得到最大似然的估计
a.
根据直方图可以看到,gamma分布十分合理
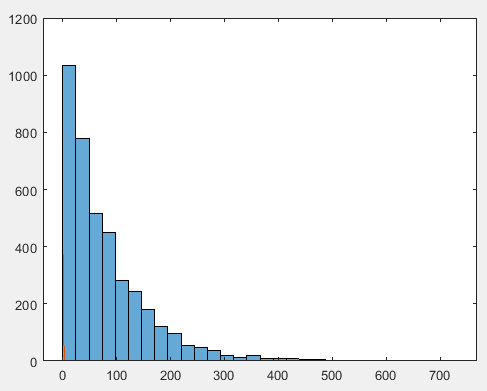
b.
矩估计拟合参数:
a =
1.0124
b =
78.9599
最大似然拟合参数:
Parameter Estimate Std. Err.
a 1.02633 0.0204199
b 77.8844 1.97566
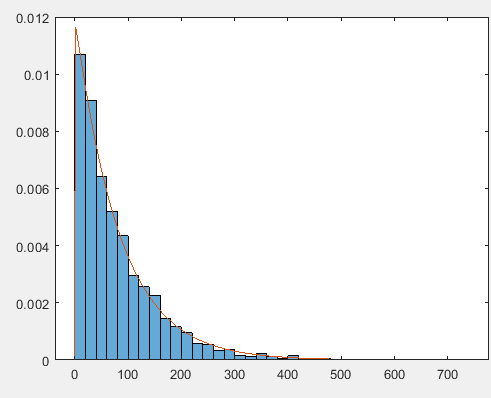
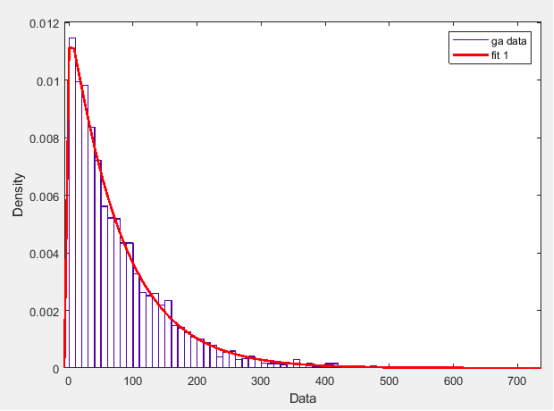
c.
我看起来肥肠合理

d.
M=1000;%进行1000次抽样 n=100;%抽取容量为100的样本 a=1.0124;%设置矩估计的gamma函数的初始值 b=78.9599;%设置矩估计的gamma函数的初始值 a_=1.02633; b_=77.8844; a0=[];%定义空数组 b0=[];%定义空数组 for i=1:M%开始循环 data=gamrnd(a,b,n,1);%随机抽取n个样本 x_=mean(data);%取n个样本的均值 v_=var(data,1);%取n个样本的方差 a1=x_^2/v_;%根据书中的对形状参数的估计公式得出a1 b1=v_/x_;%书中lambda的估计是尺度参数的倒数,也就是逆尺度参数(https://baike.baidu.com/item/伽马分布/7245468?fr=aladdin) a0=[a0 a1];%把循环得到的a1放入a0数组 b0=[b0 b1];%把循环得到的b1放入b0数组 end figure subplot(2,2,1:2) histogram(a0,10)%对a的抽样分布进行画图 subplot(2,2,3:4) histogram(b0,10)%对b的抽样分布进行画图 s_a=std(a0,1) s_b=std(b0,1)
矩估计参数分布:
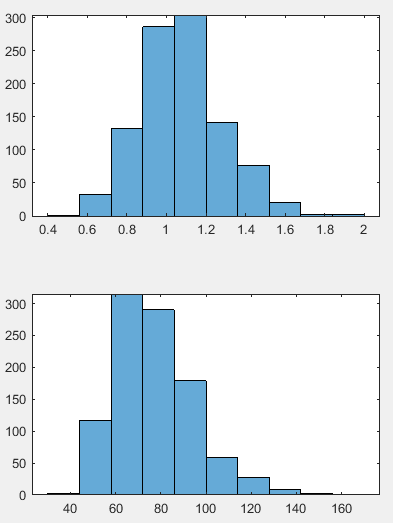
最大似然估计参数分布:

自助法1000次抽样样本容量为100的样本:
矩估计标准误差:
s_a =
0.1973
s_b =
17.6566
最大似然标准误差:
s_a =
0.1987
s_b =
16.0941
两者难分伯仲。
e.
自助法矩估计参数95%置信区间:
btm1 =
0.6814
up1 =
1.4550
btm2 =
42.9916
up2 =
112.2041
自助法最大似然估计参数95%置信区间:
btm1 =
0.6976
up1 =
1.4766
btm2 =
44.3785
up2 =
107.4661
两者差别不大,似乎最大似然好一点。
f.
不会
P224-47(a)(b)
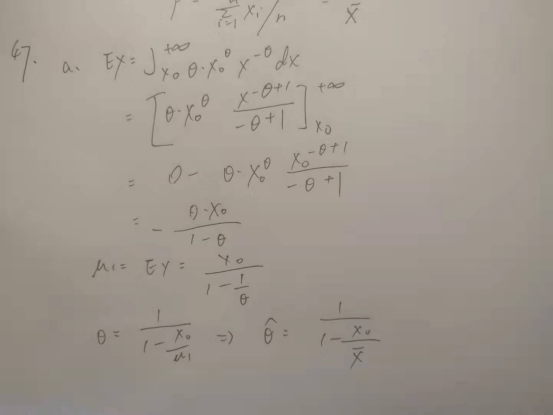



 浙公网安备 33010602011771号
浙公网安备 33010602011771号