数理统计与数据分析-hw2
习题7.7
15,
a,
%医院总数为393所以设N=393 %以n为变量去作图p和n的关系式 %其中s为总体的方差经计算为589.7 %s1的即样本均值的方差的,根据书中p149页公式计算得到 %公式:s1=(s*sqrt(N-n))./sqrt(n*(N-1)) %其中./是为了保证n向量的按位相除可以得到p的向量形式结果 %p的关系中是以200./s1为变量的标准正态分布,所以把normcdf() %公式做出经计算的分布函数的图像就可以 N=393 n=10:1:100 s=sqrt(var(hospitals.discharges)) s1=(s*sqrt(N-n))./sqrt(n*(N-1)) p=2*(1-normcdf(200./s1,0,1)) figure plot(n,p,'-')
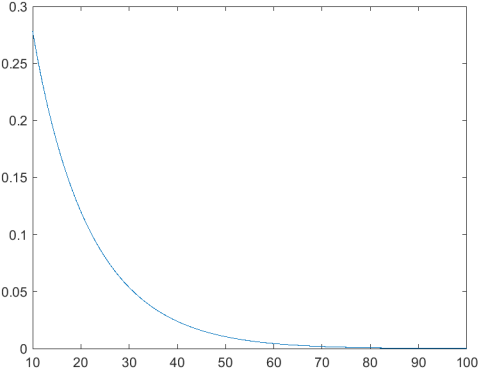
b,
%计算得到delta的办法是使用norminv函数求得 %0.10时的正态的位置,由于是双边的所以取0.95 %乘上之前得到的s1就可以得到答案 N=393 n=20 s=sqrt(var(hospitals.discharges)) s1=(s*sqrt(N-n))./sqrt(n*(N-1)) delta=s1*norminv(0.95,0,1)
n=20时
delta =
211.5765
n=40时
delta =
145.5410
n=60时
delta =
115.4183
P=0.5时
n=20,40,60的情况分别是
delta =
86.7592 59.6806 47.3285
21,
由于置信区间的宽度等于样本方差和z(α/2)的乘积,z(α/2)在95%的置信度下基本不变,所以样本方差中的参数n会发生改变,如果样本方差变为之前的1/2,那么n后=4n前/(1+2n前/N)。不考虑修正系数的话是原来的4倍。

22 ,

47,
%如果需要查看结果可以去掉句尾的分号,不需要加上分号即可 N=393%样本总数为393 n=128%抽样样本数为64/128 M=500%500次抽样 data=[]%空矩阵 for i=1:M%for循环开始 index1=randperm(numel(hospitals)/2);%用randperm函数对hospitala数据的行数进行打乱重排得到一组乱序数 hos=hospitals(index1(1:n),:);%从hospitals数据表格中抽取n条数据放入hos表格中以便后面调用数据,而不是重复抽取导致数据驴唇不对马嘴 data(i,1)=mean(hos.discharges);%对第一列的数据求均值放入data矩阵的第i行第1列 data(i,2)=mean(hos.beds);%对第二列的数据求均值放入data矩阵的第i行第2列 end mux=mean(hospitals.beds);%计算总体的床位的均值mux muy=mean(hospitals.discharges);%计算总体的出院人数的均值muy r=muy/mux;%计算总体的比率r varx=var(hospitals.beds);%计算x的方差 vary=var(hospitals.discharges);%计算y的方差 sx=std(hospitals.beds);%计算x的标准差 sy=std(hospitals.discharges);%计算y的标准差 sxy=sum((hospitals.beds-mux).*(hospitals.discharges-muy))/N;%计算x和y 的总体协方差 rou=sxy/(sx*sy);%计算总体相关系数 yr=(data(:,1)./data(:,2))*mux;%计算Y_R ey=mean(yr)%计算E(Y_R) bias=(N-n)*(r*varx-rou*sx*sy)/((N-1)*n*mux) %muy比率估计的近似偏倚 bias1=ey-muy%样本容量为n的500个出院人数均值的比率估计的偏倚 s1=std(data(:,1))%样本容量为n的500个出院人数均值的简单随机估计的标准差 s2=std(yr)%样本容量为n的500个出院人数均值的比率估计的标准差 vary=(N-n)*(r^2*varx+vary-2*r*rou*sx*sy)/(n*(N-1)); sy=sqrt(vary) figure subplot(2,2,1:2) histogram(data(:,1),20)%复现图7.6(a subplot(2,2,3:4) histogram(yr,20)%复现图7.6(b
n=64的样本中推论7.4.2的Y_R的近似偏倚为
bias =
0.9803
E(Y_R)-muy的值为
bias1 =
0.7537
估计的近似标准差为
sy =
30.2861
其中抽样500次的简单随机样本和比率估计的标准差分别为:
s1 =
66.0579
s2 =
30.0280
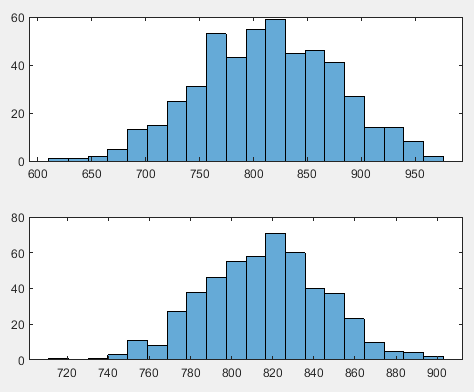
n=128的样本中推论7.4.2的Y_R的近似偏倚为
bias =
0.3948
E(Y_R)-muy的值为
bias1 =
0.0733
估计的近似标准差为
sy =
19.2200
其中抽样500次的简单随机样本和比率估计的标准差分别为:
s1 =
42.1647
s2 =
19.3754
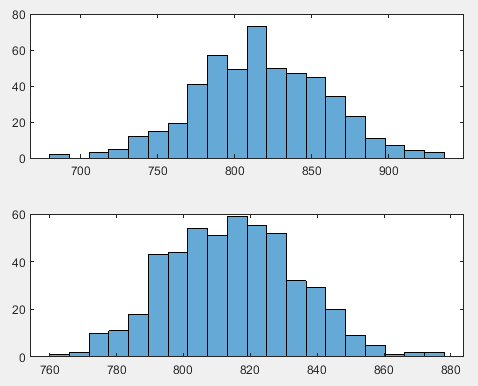
48,
n=100;%抽样样本的数量:100个城市家庭 N=100000;%城市家庭共有100000户 sumx=320;%x的加和值为320 sumy=10000;%y的加和值为10000 sumx2=1250;%x^2的加和值为1250 sumy2=1100000;%y^2的加和值为1100000 sumxy=36000;%xy的加和值为36000 r_=sumy/sumx%估计比率r的估计值 sxy=(sumxy-n*(sumx/n)*(sumy/n))/(n-1);%样本协方差 sx=sqrt((sumx2-n*(sumx/n)^2)/n);%x样本的标准差 sy=sqrt((sumy2-n*(sumy/n)^2)/n)%y样本的标准差 rou_=sxy/(sx*sy)%rou样本相关系数的计算 varr_=(N-n)*((r_^2)*sx^2+sy^2-2*r_*sx*sy)/(n*(N-1)*(sumx/n)^2);%样本的估计方差 sr_=sqrt(varr_)%样本的估计标准差 up=r_+norminv(0.975,0,1)*sr_%置信区间的上区间 btm=r_-norminv(0.975,0,1)*sr_%置信区间的下区间
- 估计比率r_:
r_ =
31.2500
- 置信区间的上界和下界分别是:
up =
32.1901
btm =
30.3099
- 周食物支出的90%置信区间的下界和上界分别是:
btm =
9.4799e+03
up =
1.0520e+04
n=100;%抽样样本的数量:100个城市家庭 N=100000;%城市家庭共有100000户 sumy=10000;%y的加和值为10000 sumy2=1100000;%y^2的加和值为1100000 vary=n*(sumy2-n*(sumy/n)^2) ssumy=sqrt((sumy2-n*(sumy/n)^2)) btm=sumy-norminv(0.95,0,1)*ssumy%置信区间的下区间 up=sumy+norminv(0.95,0,1)*ssumy%置信区间的上区间
65 a~k,
a.
clear all cancer=importdata('cancer.txt');%载入数据cancer的数据 data=cancer(:,1);%读取第一列的数据放入data figure histogram(data)%画出直方图

b.
cancer=importdata('cancer.txt');%载入数据cancer的数据 data=cancer(:,1);%读取第1列的数据放入data mean1=mean(data)%均值 sum1=sum(data)%总数 var1=var(data)%方差 s1=std(data)%标准差
癌症死亡人数的总体均值、总数、方差和标准差分别是:
mean1 =
39.8571
sum1 =
11997
var1 =
2.5987e+03
s1 =
50.9778
c.
N=301;%有N条数据 n=25;%每次抽样的数量为n M=500;%进行M次重复独立实验 for i=1:M index1=randperm(N);%用randperm函数对cancer数据的行数进行打乱重排得到一组乱序数 data=[data mean(cancer(index1(1:n),1))];%把得到的抽样数据放进data end figure histogram(data)%画出直方图
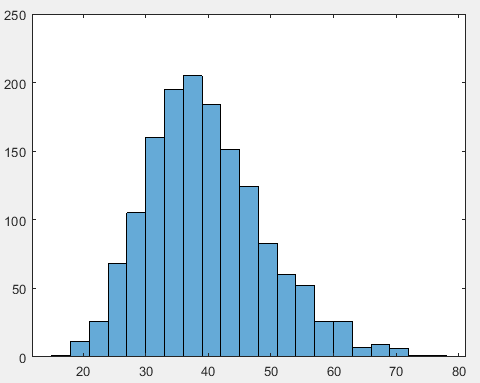
d.
cancer=importdata('cancer.txt');%载入数据cancer的数据 N=301;%有N条数据 n=25;%每次抽样的数量为n M=500;%进行M次重复独立实验 data=[];%定义经矩阵data for i=1:M index1=randperm(N);%用randperm函数对cancer数据的行数进行打乱重排得到一组乱序数 data=[data mean(cancer(index1(1:n),1))];%把得到的抽样数据放进data end mean(data) T=mean(data)*N
对500次抽取的25个样本的均值求期望得到总体均值的估计为:39.7469。总数的估计为:1.2143e+04。
e.
cancer=importdata('cancer.txt');%载入数据cancer的数据 N=301;%有N条数据 n=25;%每次抽样的数量为n M=500;%进行M次重复独立实验 data=[];%定义经矩阵data for i=1:M index1=randperm(N);%用randperm函数对cancer数据的行数进行打乱重排得到一组乱序数 data=[data mean(cancer(index1(1:n),1))];%把得到的抽样数据放进data end var2=var(data) s2=std(data)
对500次抽取的25个样本的均值求期望得到总体均值方差和标准差的估计分别为:
var2 =
95.9180
s2 =
9.7938
f.
95%置信区间的下界和上界分别是:
btm =
20.8164
up =
59.0962
包含总体值。
g.
cancer=importdata('cancer.txt');%载入数据cancer的数据 N=301;%有N条数据 n=100;%每次抽样的数量为n M=500;%进行M次重复独立实验 data=[];%定义经矩阵data for i=1:M index1=randperm(N);%用randperm函数对cancer数据的行数进行打乱重排得到一组乱序数 data=[data mean(cancer(index1(1:n),1))];%把得到的抽样数据放进data end mean2=mean(data) T=mean(data)*N var2=var(data) s2=std(data) btm=mean2-norminv(0.975,0,1)*s2 up=mean2+norminv(0.975,0,1)*s2
结果:
mean2 =
40.2013
T =
1.2101e+04
var2 =
17.1437
s2 =
4.1405
btm =
32.0861
up =
48.3165
h.
这个方法可能有效,因为县的总人口通常通过女性人口的占比多少来影响乳腺癌发病人数。所以通过计算总人口和患癌死亡人数的变异系数与两者相关系数的比较大小才能确定是否可以通过总人口的比率估计得出有效的结论。
i.
cancer=importdata('cancer.txt');%载入数据cancer的数据 N=301;%有N条数据 n=25;%每次抽样的数量为n M=500;%进行M次重复独立实验 data=[];%定义经矩阵data for i=1:M index1=randperm(N);%用randperm函数对cancer数据的行数进行打乱重排得到一组乱序数 can=cancer(index1(1:n),:);%把得到的抽样数据放进data data(i,1)=mean(can(:,1));%对第一列的数据求均值放入data矩阵的第i行第1列 data(i,2)=mean(can(:,2));%对第二列的数据求均值放入data矩阵的第i行第2列 end mux=mean(cancer(:,2));%计算总体的女性人口数的均值mux muy=mean(cancer(:,1))%计算总体的癌症死亡人数的均值muy r=muy/mux;%计算总体的比率r varx=var(cancer(:,2));%计算x的方差 vary=var(cancer(:,1));%计算y的方差 sx=std(cancer(:,2));%计算x的标准差 sy=std(cancer(:,1));%计算y的标准差 sxy=sum((cancer(:,2)-mux).*(cancer(:,1)-muy))/N;%计算x和y 的总体协方差 rou=sxy/(sx*sy);%计算总体相关系数 yr=(data(:,1)./data(:,2))*mux;%计算Y_R ey=mean(yr)%计算E(Y_R) bias=(N-n)*(r*varx-rou*sx*sy)/((N-1)*n*mux) %muy比率估计的近似偏倚 bias1=ey-muy%样本容量为n的500个癌症死亡人数均值的比率估计的偏倚 s1=std(data(:,1))%样本容量为n的500个癌症死亡人数均值的简单随机估计的标准差 s2=std(yr)%样本容量为n的500个癌症死亡人数均值的比率估计的标准差 vary=(N-n)*(r^2*varx+vary-2*r*rou*sx*sy)/(n*(N-1)); sy=sqrt(vary) figure subplot(2,2,1:2) histogram(data(:,1),20) subplot(2,2,3:4) histogram(yr,20)
样本数为25的比率估计量的抽样分布:(上图为样本容量为25的500个癌症死亡人数的简单随机估计直方图,下图为样本容量为25的500个癌症死亡人数的比率估计直方图)

其计算结果为:
s1 =
9.2789
s2 =
2.4147
比率估计的标准差显著小于简单随机估计的标准差。
j.
同一组抽样数据中d的估计为:
ey1 =
40.2878
T1 =
1.2127e+04
比率估计得出的是:
ey2 =
39.9347
T2 =
1.2020e+04
其中,总体的均值和总数分别为:
mean1 =
39.8571
sum1 =
11997
可知,比率估计的均值和总数更接近于总体的均值和方差。
k.
简单随机抽样的95%的置信区间的上下界和比率估计的95%的置信区间的上下界分别是:
btm1 =
20.5058
up1 =
58.3555
btm2 =
34.6944
up2 =
44.6762
l.
cancer=importdata('cancer.txt');%载入数据cancer的数据 N=301;%有N条数据 n=16;%每次抽样的数量为n S=4;%分层抽样分为4层 data=[];%定义空矩阵data用于存储抽样得到的数据 mu=[];%定义空矩阵mu用于存储每层得到的总体均值数据 s=[] nl=[] x_s=[];%定义空矩阵_s用于存储每层得到的均值*层比例的数据用于最后的加总 for i=1:S if i<S index1=randperm(75);%1:3层每层75打乱顺序 can=cancer(ceil((i-1)*300/S)+index1(1:n),:);%在每层中抽取n个观察值 data=[data can];%存储得到的观察值数据 mu=[mu mean(cancer(ceil((i-1)*300/S)+index1,1))];%存储每层的均值数据 s=[s std(cancer(ceil((i-1)*300/S)+index1,1))] x_s=[x_s 75*mean(data(:,2*i-1))/301]%存储前3层均值*层比例的数据 else index1=randperm(76);%4层76条数据打乱顺序 can=cancer(ceil((i-1)*300/S)+index1(1:n),:);%抽取n个观察值 data=[data can];%存储得到的观察值数据 mu=[mu mean(cancer(ceil((i-1)*300/S)+index1,1))];%存储4层的均值数据 s=[s std(cancer(ceil((i-1)*300/S)+index1,1))] x_s=[x_s 76*mean(data(:,2*i-1))/301]%存储第4层均值*层比例的数据 end end mux=mean(cancer(:,1))%总体均值真实值 T=sum(cancer(:,1))%总体总数真实值 X_S=sum(x_s)%样本估计的总体均值 TS=N*X_S%样本估计的总体总数
死亡人数的总体均值和总数的真实值:
mux =
39.8571
T =
11997
死亡人数的总体均值和总数的样本估计值:
X_S =
41.2087
TS =
1.2404e+04
m.
wl=[75/301,75/301,75/301,76/301] down=sum(s.*wl) for i=1:S if i<S nl(1,i)=round(n*S*(75*s(1,i)/301)/down); else nl(1,i)=round(n*S*(76*s(1,i)/301)/down); end end nl
如果总共抽取样本64个,那么比例分配的抽样比例是:16/75,16/75,16/75,16/76.最优分配的抽样比是:3/75,5/75,9/75,48/75.
var_all=var(cancer(:,1)) var_xs=var_all*(N-n*S)/(n*(N-1)) var_so=power(down,2)/(n*S) var_sp=sum(wl.*power(s,2))/(n*S)
简单随机抽样、比例分配和最优分配三种方法得到的总体均值估计的方差分别是:
var_xs =128.3126
var_so = 8.3383
var_sp =19.2759
可见比例分配对于简单随机抽样的方差降低十分明显,而最优分配对于比例分配的方差也有所改善。
n
假设总体分层抽样共抽取64个样本,4层的话每层16个样本;8层的话每层8个样本;16层的话每层4个样本;32层的话每层2个样本;64层的话每层1个样本。代入估计可得:
8层:
var_xs =256.6252
var_so =4.5543
var_sp =13.5653
16层:
var_xs =513.2504
var_so =2.1297
var_sp =5.5788
32层:
var_xs =1.0265e+03
var_so =2.2526
var_sp =5.1518
64层:
不会算。
事实证明,层数越多,改进的空间也会越小。
67 .
a.
families=importdata('families.txt');%载入families数据集 fam=families.data;%提取数据集中的数据部分 N=43886;%数据集中数据总数为N n=500;%样本数为n fm=[];%fm空矩阵用于存取抽取的数据 for i=1:n%for循环开始 index1=randperm(N);%打乱顺序 fm=fam(index1(1:n),:);%抽取n个数据 end p_=sum(fm(:,1)==3)/n%得到总体比例的估计:样本比例 sp_=p_*(1-p_)*(1-n/N)/(n-1)%通过方差公式得到样本方差 btm1=p_-norminv(0.975,0,1)*sp_%95%置信区间的下界 up1=p_+norminv(0.975,0,1)*sp_%95%置信区间的上界 baby_=mean(fm(:,3)) sbaby_=std(fm(:,3))*(N-n)/(n*(N-1)) btm2=baby_-norminv(0.975,0,1)*sbaby_ up2=baby_+norminv(0.975,0,1)*sbaby_ edu_=sum(fm(:,6)<39)/n sedu_=edu_*(1-edu_)*(1-n/N)/(n-1) btm3=edu_-norminv(0.975,0,1)*sedu_ up3=edu_+norminv(0.975,0,1)*sedu_ inc_=mean(fm(:,4)) sinc_=std(fm(:,4))*(N-n)/(n*(N-1)) btm4=inc_-norminv(0.975,0,1)*sinc_ up4=inc_+norminv(0.975,0,1)*sinc_
其中,女户主家庭所占比例、每户家庭的平均孩子数、家庭户主没有高中毕业证书的比例和平均家庭收入的总体估计、标准误差和95%置信区间的下界和上界分别是:
p_ =0.1960
sp_ = 3.1220e-04
btm1 =0.1954
up1 =0.1966
baby_ =0.9320
sbaby_ =0.0023
btm2 =0.9275
up2 =0.9365
edu_ =0.1960
sedu_ =3.1220e-04
btm3 = 0.1954
up3 =0.1966
inc_ =4.3030e+04
sinc_ =67.2945
btm4 =4.2898e+04
up4 =4.3162e+04
b.
families=importdata('families.txt');%载入families数据集 fam=families.data;%提取数据集中的数据部分 N=43886;%数据集中数据总数为N n=400;%样本数为n M=100%抽取M个容量为n 的样本 fm=[];%fm空矩阵用于存取抽取的数据 inc=[]%income的空矩阵 for i=1:M%for循环开始 index1=randperm(N);%打乱顺序 fm=fam(index1(1:n),:);%抽取n个数据 inc=[inc mean(fm(:,4))];%放入每组的income均值 end x=37000:10:46000;%用于正态分布的绘图 mean1=mean(inc)%mean1是样本收入均值 s1=std(inc)%s1为样本标准差 figure subplot(2,2,1:2) plot(x,normcdf(x,mean1,s1))%画出正态分布图 hold on cdfplot(inc)%画出累计分布图 subplot(2,2,3:4) histogram(inc,y)%画出直方图 histfit(inc)%画出正态分布拟合图 figure normplot(inc)%画出正态概率图
100个估计的平均数和标准差为:
mean1 =
4.1416e+04
s1 =
1.5526e+03
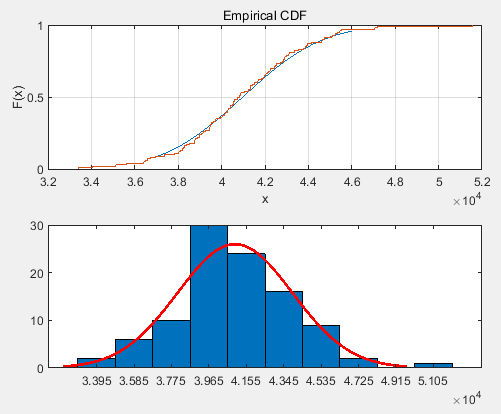
经验累积分布函数叠加正态累计分布函数,和直方图叠加同均值和标准差的正态密度线:

正态概率图:
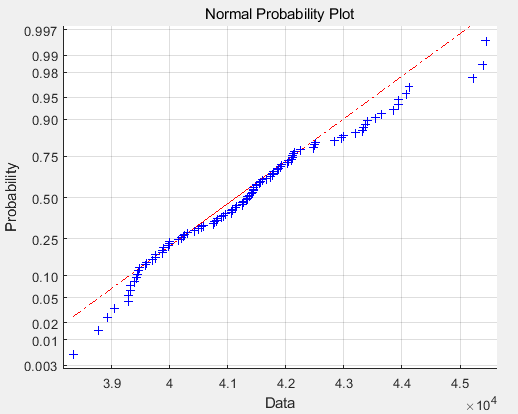
b1=sum(power((inc-mean1),3))/(n*power(s1,3))
偏度系数b1为:
b1 =
0.0817
100个容量100的样本:
经验累积分布函数叠加正态累计分布函数,和直方图叠加同均值和标准差的正态密度线:
正态概率图:
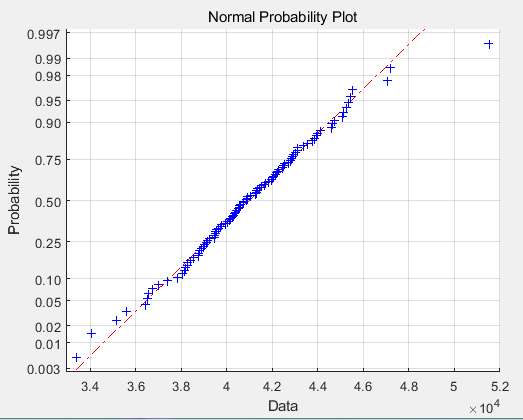
偏度系数b1为:
b1 =
0.3604
c.
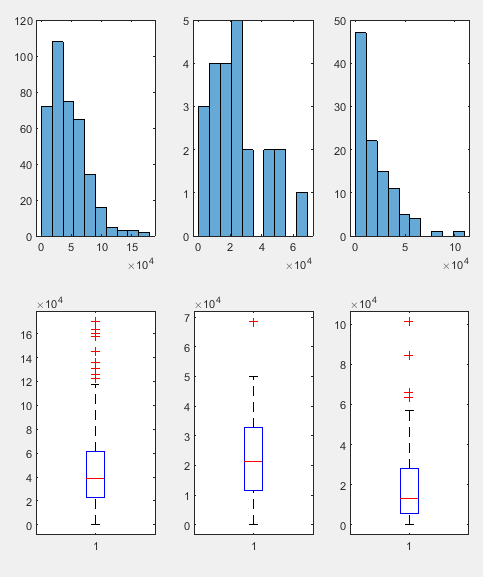
families=importdata('families.txt');%载入families数据集 fam=families.data;%提取数据集中的数据部分 N=43886;%数据集中数据总数为N n=500;%样本数为n fm=[];%fm空矩阵用于存取抽取的数据 f=[];%f空矩阵用于装i类型家庭的收入数据 figure for i=1:3%for循环开始 index1=randperm(N);%打乱顺序 fm=fam(index1(1:n),:);%抽取n个数据 index2=find(fm(:,1)==i);%找到第i个类型家庭的索引 f=fm(index2,4);%用索引找到i类家庭的收入 subplot(2,3,i)%子图 histogram(f,10)%画直方图 subplot(2,3,i+3) boxplot(f)%箱线图 f=[]; end
直方图和箱线图:
d.
families=importdata('families.txt');%载入families数据集 fam=families.data;%提取数据集中的数据部分 N=43886;%数据集中数据总数为N n=400;%样本数为n fm=[];%fm空矩阵用于存取抽取的数据 f=[];%f空矩阵用于装i类型家庭的收入数据 figure for i=1:4%for循环开始 index1=randperm(N);%打乱顺序 fm=fam(index1(1:n),:);%抽取n个数据 index2=find(fm(:,5)==i);%找到第i个分区的索引 f=fm(index2,4);%用索引找到i分区的收入 subplot(2,4,i)%子图 histogram(f,10)%画直方图 subplot(2,4,i+4) boxplot(f)%箱线图 f=[]; end
收入:

家庭规模:北区和西区的家庭规模会大于东区和南区。
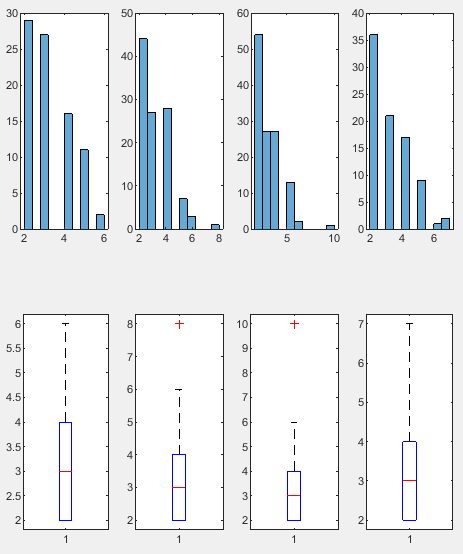
教育程度:南区和西区的教育程度会高于东区和北区。
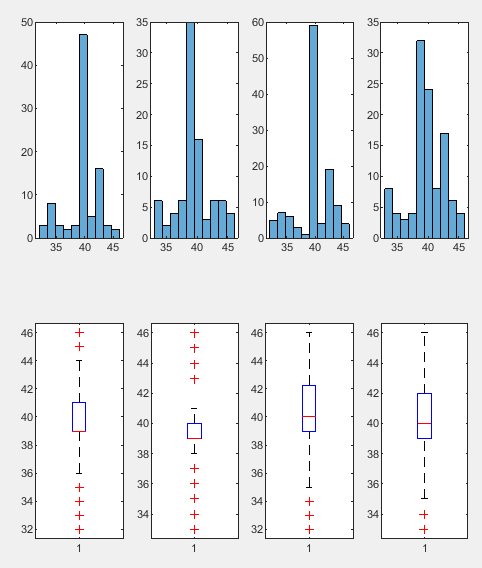
e.
每个地区的生育意愿有差别吗?
可以看到西区的生育意愿高于其他区。
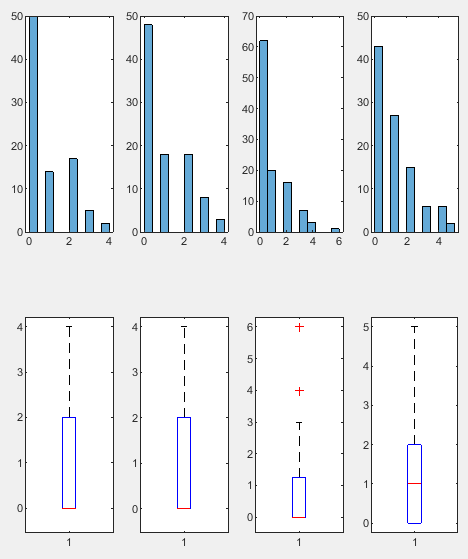
f.
400简单随机样本估计平均收入:
分层样本估计平均收入:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号