数理统计与数据分析-hw1
5章-习题5.4
13

Matlab:
m=60 n=1000 r=binornd(1,0.5,m,n)-0.5 z=sum(r)*100 figure histfit(z)
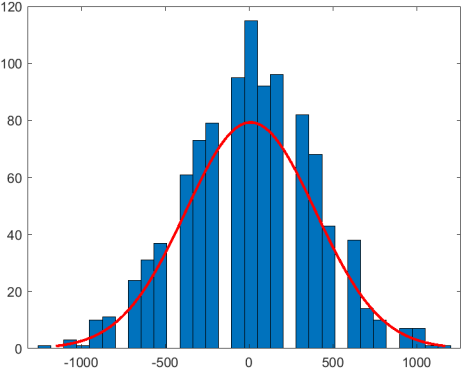
19.
a.
N=100: n=100 x=rand(n,1) f=cos(2*pi*x) I=sum(f)/n
结果:
I =
-0.0179
1000次对n=100的蒙特卡洛方法的结果的分布拟合:
n=100 x=rand(n,1000) f=cos(2*pi*x) I=sum(f)/n figure histfit(I)

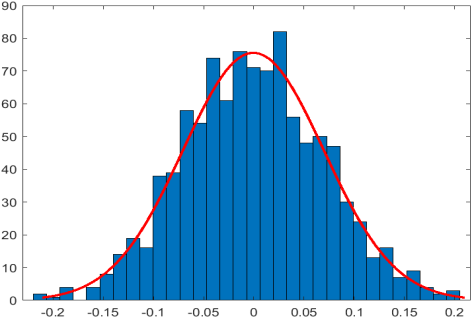
N=1000:
I =
0.0109
1000次对n=1000的蒙特卡洛方法的结果的分布拟合:

通过以上两种n=100和n=1000的蒙特卡洛方法的多次试验可以知道两种都可以得到精确答案0的近似结果,但是无法完全得到精确答案,而且多次试验的曲线拟合是均值为0的某种正态分布,可以看出来n=1000比n=100得到的结果对精确答案的偏差更小,更集中。
b.
通过积分计算器可以得到
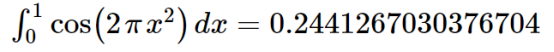
1000次蒙特卡洛方法得到的近似值是I = 0.2183
多次蒙特卡洛方法得到的分布拟合曲线是:

可以近似,但是依然无法得到精确值。
20.
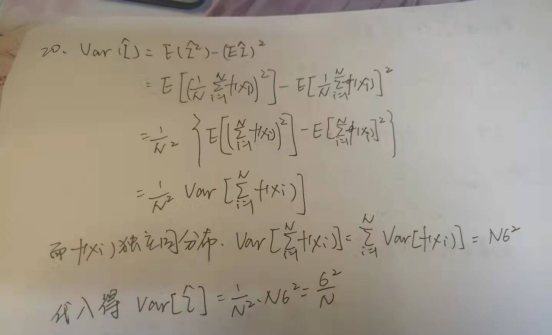
19.a.中cos(2*pi*x)的方差经计算为1/2,则Var(I)的估计标准差为√(1/2000),约等于0.02236067977,n=100和n=1000的实际误差分别是0.0708,0.0201。所以蒙特卡洛采取的样本点越多实际的误差越接近与估计标准差。
n=1000 x=rand(n,100) f=cos(2*pi*x) I=sum(f)/n s=std(I)
30.
a. Sn
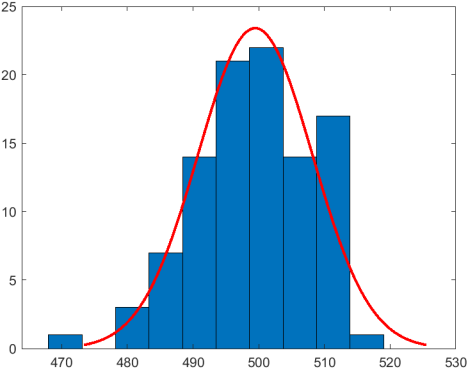
b. Sn/n

c. Sn-n/2

d. (Sn-n/2)/n

e. (Sn-n/2)/√n
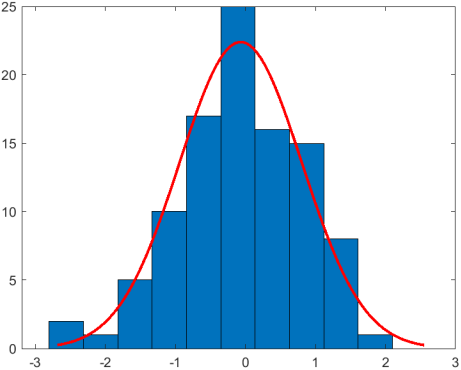
其中,绘图采取生成100组的1000个0和1之间的均匀随机变量进行加和得到Sn并对其进行统计,拟合,得到不同的曲线。
Sn的曲线是以500为均值,方差为1000/12(标准差约为9.1)的正态曲线。
Sn/n的曲线是以0.5为均值,方差为1/12000(标准差约为0.009)的正态曲线。
Sn-n/2的曲线是以0为均值,方差为1000/12(标准差约为9.1)的正态曲线。
(Sn-n/2)/n的曲线是以0为均值,方差为1/12000(标准差约为0.009)的正态曲线。
(Sn-n/2)/√n的曲线是以0为均值,方差为1/12(标准差约为0.083)的正态曲线。
6章
1、生成t分布与F分布的随机数,并画图
T分布:

n=1000 N=10 u=randn(N,n) z=randn(1,n) chi2=sum(u.^2) t=z./(sqrt(chi2/N)) histogram(t)
F分布:

n=1000 M=10 N=10 u=randn(M,n) v=randn(N,n) chi1=sum(u.^2) chi2=sum(v.^2) f=(chi1/M)./(chi2/N) histogram(f)
2、复现图6.1

x=-3:0.01:3 t1=tpdf(x,5) t2=tpdf(x,10) t3=tpdf(x,30) z=normpdf(x,0,1) figure plot(x,t1,'-.',x,t2,':',x,t3,'--',x,z,'-') axis([-3,3,0,0.4]) legend('自由度为5','自由度为10','自由度为30','标准正态分布')
3、仿真验证习题6,7,8
习题6
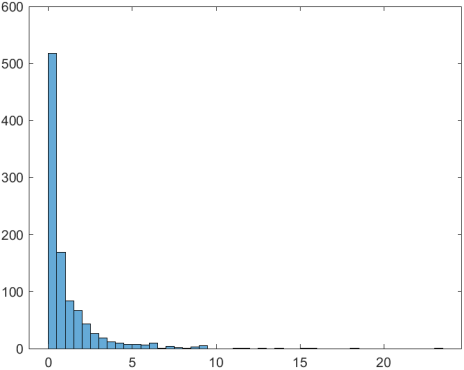
n=1000 N=10 u=randn(N,n) z=randn(1,n) chi2=sum(u.^2) t=z./(sqrt(chi2/N)) T=t.^2 histogram(T)

x=0:0.01:10 n=10 f=fpdf(x,1,n) figure plot(x,f,'--') axis([-1,25,0,4]) legend('自由度为1,n的f分布')
习题7
x=-3:0.01:3 t1=tpdf(x,1) c=1./(pi*(1+x.^2)) figure subplot(2,2,1:2) plot(x,t1,'-.') axis([-3,3,0,0.4]) legend('自由度为1的t分布') subplot(2,2,3:4) plot(x,c,'-') axis([-3,3,0,0.4]) legend('柯西分布')
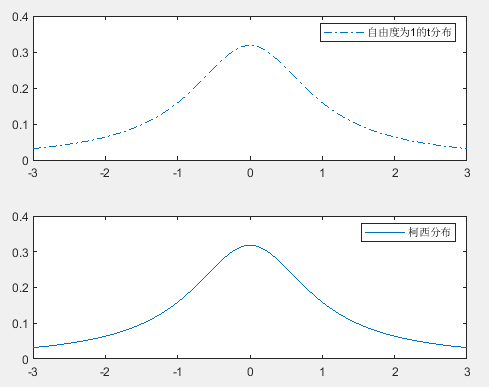
习题8
不会写,随便画的。
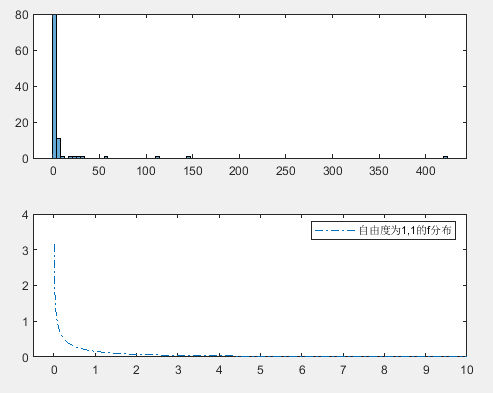
clear all a=0:0.01:10 x=exprnd(1,1,100) y=exprnd(1,1,100) z=x./y f=fpdf(a,1,1) figure subplot(2,2,1:2) histogram(z,100) subplot(2,2,3:4) plot(a,f,'-.') axis([-0.5,10,0,4]) legend('自由度为1,1的f分布')
7章-用数据hospitals生成简单随机样本,复现7.3节:
图7.2
其中一个代码:
N=393%医院总数为393 n=8%一次抽样抽n个 M=500%做500次重复独立实验 data=[]%定义空矩阵装数据 for i=1:M%for循环 index1=randperm(numel(hospitals)/2);%打乱行顺序 data=[data mean(hospitals(index1(1:n),:).discharges)];%N个数据中随机抽取n个数据 end figure histogram(data)%画图
A.n=8
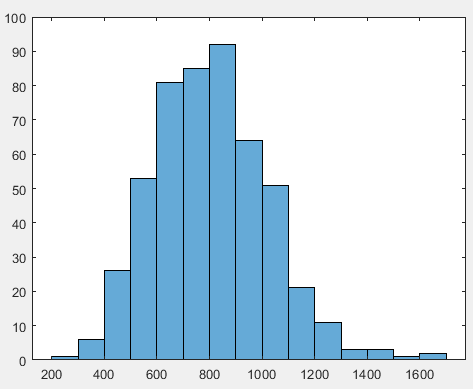
B.n=16

C.n=32
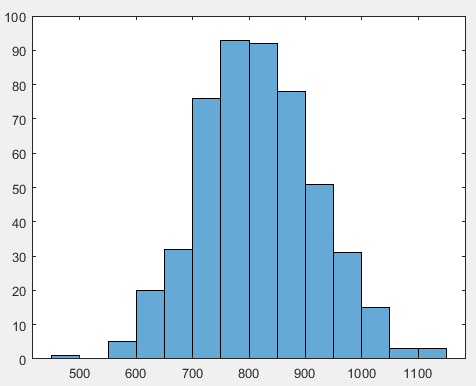
D.n=64

例7.3.1.2-3
7.3.1.2
抽样的样本均值的方差为:
s =
99.5562
代码:
N=393%医院总数为393 n=8%一次抽样抽n个 M=500%做500次重复独立实验 data=[]%定义空矩阵装数据 for i=1:M%for循环 index1=randperm(numel(hospitals)/2);%打乱行顺序 data=[data mean(hospitals(index1(1:n),:).discharges)];%N个数据中随机抽取n个数据 end v=var(data) s=sqrt(v)
总体样本的标准差为:
s =
589.7173
代码:
v=var(hospitals.discharges) s=sqrt(v)
符合例7.3.1.2所描述
7.3.1.3
总体样本的比例为:
p =
0.6539
代码:
p=sum(hospitals.discharges<1000)/N
样本的比例的方差为:
s =
0.0817
代码:
N=393%医院总数为393 n=32%一次抽样抽n个 M=500%做500次重复独立实验 data=[]%定义空矩阵装数据 for i=1:M%for循环 index1=randperm(numel(hospitals)/2);%打乱行顺序 data=[data sum(hospitals(randi(N,1,n),:).discharges<1000)/n];%N个数据中随机抽取n个数据 end s=std(data)
例7.3.2.1-3
7.3.2.1
容量为50的简单随机样本的方差和标准差分别是:
v =
7.7610e+03
s =
88.0967
代码:
N=393%医院总数为393 n=50%一次抽样抽n个 M=500%做500次重复独立实验 data=[]%定义空矩阵装数据 for i=1:M%for循环 index1=randperm(numel(hospitals)/2);%打乱行顺序 data=[data mean(hospitals(randi(N,1,n),:).discharges)];%N个数据中随机抽取n个数据 end v=var(data) s=sqrt(v)
7.3.2.2
总人数估计的标准差为:
s =
4.2676e+03
代码:
N=393%医院总数为393 n=50%一次抽样抽n个 M=500%做500次重复独立实验 data=[]%定义空矩阵装数据 for i=1:M%for循环 index1=randperm(numel(hospitals)/2);%打乱行顺序 data=[data sum(hospitals(randi(N,1,n),:).discharges)];%N个数据中随机抽取n个数据 end v=var(data) s=sqrt(v)
7.3.2.3
出院人数少于1000的医院比例的p的标准差为:
s =
0.0687
代码:
N=393%医院总数为393 n=50%一次抽样抽n个 M=500%做500次重复独立实验 data=[]%定义空矩阵装数据 for i=1:M%for循环 index1=randperm(numel(hospitals)/2);%打乱行顺序 data=[data sum(hospitals(randi(N,1,n),:).discharges<1000)/n];%N个数据中随机抽取n个数据 end v=var(data) s=sqrt(v)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号