KMP——强大的next数组
\(KMP\) 的原理不在这里仔细讲了,主要说说最近刷题总结出的 \(next\) 数组的强大功能。
部分例题来自《信息学奥赛一本通》的配套练习。
基于定义——字符串相同前后缀
“基于定义”:我们求的 \(next\) 数组就是字符串到某一位时最长相同前后缀的长度。
注意 \(next\) 数组求的为“最长”的,那如果想知道一个字符串所有相同的前后缀长度咋办?
举个栗子:
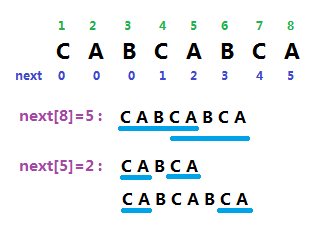
假设一个 \(n\) 位的字符串(下标从 \(1\) 到 \(n\)),\(next[n]=p\)
那么该字符串的子串 \([1,p]\) 与 \([n-p+1,n]\) 应是相同的
设 \(next[p]=q\) ,那么子串 \([1,q]\) 与 \([p-q+1,p]\) 是相同的
综上,子串 \([1,q]\) 与 \([n-q+1,n]\) 是相同的,即 \(next[next[n]]\) 也是该字符串相同前后缀长度
就这样 \(next\) 一遍遍向前找,直到某一位的 \(next\) 为 \(0\), 拓展出一棵 \(next\) 树(也叫 \(fail\) 树)。
例题 \(bzoj3620\)
\(PROBLEM:\)
求一个长度为 \(n\) 的字符串所有形似 \(A+B+A\) , 且 \(len(A) \geq k,len(B) \geq 1\) 的子串数目。
\(n \leq 15000\)
\(SOLUTION:\)
一个奇妙的事情是这个题 \(O(n^2)\) 能过。
于是枚举每一位为起点,\(KMP\) 的过程中,\(next\) 值相当于这一段子串 \(len(A)\) 的最大值
如果它小于 \(k\) ,显然不行。
而若 \(它 \times 2+1 > 子串长度\) 也不行。
所以需要找到合适的 \(len(A)\) 满足 \(len(A) \geq k\) 且 \(len(A) \times 2 +1 \leq 子串长度\)
这就用到 \(next\) 树的思想了!
还有一个小优化,用一个数组记录某一段 \(\geq k\) 的最短的相同前后缀长度,把它作为 \(len(A)\) 判断比较快。
代码:
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 15005;
char s[N];
int nxt[N],KK,ok[N],ans;
void KMP(char p[]){
int len=strlen(p+1),k=0;
nxt[1]=0; ok[0]=ok[1]=-1;
for(int i=2;i<=len;i++){
while(k && p[i]!=p[k+1]) k=nxt[k];
if(p[i]==p[k+1]) k++;
nxt[i]=k;
if(k<KK) { ok[i]=-1; continue; }
if(ok[k]==-1) ok[i]=k;
else ok[i]=ok[k];
if(ok[i]*2+1<=i) ans++;
}
}
int main()
{
int len;
scanf("%s",s+1);
scanf("%d",&KK);
len=strlen(s+1);
for(int i=1;i<=len;i++) {
if(KK*2+1>len-i+1) break;
KMP(s+i-1);
}
printf("%d\n",ans);
return 0;
}
拓展功能——字符串循环节
“拓展”:这里的主角为 \(n-next[n]\)
还是举个栗子:
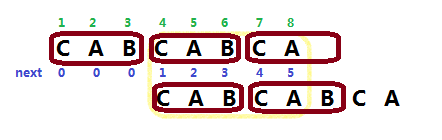
上图中 \(n-next[n]=3\) ,那 \(3\) 是什么呢?
看那些棕圈圈,\(3\) 其实可以叫做字符串的 “类”循环节,因为字符串并不是由这个循环节完完整整组成的。
而若一个字符串有真正的循环节要满足什么条件呢?
答案是 \(n-next[n]\) 整除 \(n\)
同样举个栗子就明了了:
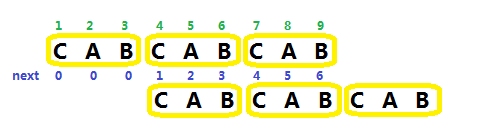
对于所有字符串, \(n-next[n]\) 只是它最短的循环节(类循环节),其他循环节(类循环节)的长度通过 \(next\) 一遍遍向前找求出。
还是 \(next\) 树的思想,结合栗子即可证明,这里就不赘述了。
!!!
注意:有真正循环节的字符串,所有循环节长度都为最短循环节长度的倍数。而类循环节并不满足这一性质!
例题1 \(bzoj1511\)
\(PROBLEM:\)
一个串是有限个小写字符的序列,特别的,一个空序列也可以是一个串. 一个串 \(P\) 是串 \(A\) 的前缀, 当且仅当存在串 \(B\) , 使得 \(A = PB\). 如果 \(P \neq A\) 并且 \(P\) 不是一个空串,那么我们说 \(P\) 是 \(A\) 的一个 \(proper\) 前缀. 定义 \(Q\) 是 \(A\) 的周期, 当且仅当 \(Q\) 是 \(A\) 的一个 \(proper\) 前缀并且 \(A\) 是 \(QQ\) 的前缀(不一定要是 \(proper\) 前缀). 比如串 \(abab\) 和 \(ababab\) 都是串 \(abababa\) 的周期. 串 \(A\) 的最大周期就是它最长的一个周期或者是一个空串(当 \(A\) 没有周期的时候), 比如说, \(ababab\) 的最大周期是 \(abab\). 串 \(abc\) 的最大周期是空串. 给出一个串,求出它所有前缀的最大周期长度之和.
\(串长度 \leq 10^6\)
\(SOLUTION:\)
其实题中说的最大周期就是 \(\neq A\) 的最长“类循环节”
\(next\) 树的思想,用一个数组记录每个“点”在该“树”上最小的非零祖先,否则会超时
#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1000005;
typedef long long ll;
int n;
int nxt[N],snxt[N];
char s[N];
int main()
{
scanf("%d",&n);
scanf("%s",s+1);
ll ans=0;
int k=0;
nxt[1]=0; snxt[1]=1;
for(int i=2;i<=n;i++){
while(k && s[i]!=s[k+1]) k=nxt[k];
if(s[i]==s[k+1]) k++;
nxt[i]=k;
snxt[i]=(k?snxt[k]:i);
ans+=i-snxt[i];
}
printf("%lld\n",ans);
return 0;
}
例题2 \(bzoj4974\)
\(PROBLEM:\)
一个串 \(T\) 是 \(S\) 的循环节,当且仅当存在正整数 \(k\),使得 \(S\) 是 \(T^k\) (即 \(T\) 重复 \(k\) 次)的前缀,比如 \(abcd\) 是 \(abcdabcdab\) 的循环节。给定一个长度为 \(n\) 的仅由小写字符构成的字符串 \(S\), 请对于每个 \(k(1 \leq k \leq n)\),求出 \(S\) 长度为 \(k\) 的前缀的最短循环节的长度 \(per_i\) 。小 \(Q\) 告诉你 \(n\) 以及 \(per_1,per_2,...,per_n\),请找到一个长度为 \(n\) 的小写字符串 \(S\),使得 \(S\) 能对应上 \(per\) 。
\(n \leq 10^5\)
\(SOLUTION:\)
可以发现,\(per_i\) 值其实就是最短“类循环节”长度,也就是 \(n-next[i]\)
于是我们可以求出所有 \(next\) 值,然后进行逆向 \(KMP\) ,得出原字符串。
代码:
#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 100005;
int n;
int nxt[N],vis[26];
char s[N];
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&nxt[i]),nxt[i]=i-nxt[i];
s[1]='a';
for(int i=2;i<=n;i++){
if(nxt[i]!=0) { s[i]=s[nxt[i]]; continue; }
for(int j=0;j<26;j++) vis[j]=0;
int k=nxt[i-1];
while(k!=0) vis[s[k+1]-'a']=1,k=nxt[k];
vis[s[k+1]-'a']=1;
for(int j=0;j<26;j++)
if(!vis[j]) { s[i]='a'+j; break; }
}
printf("%s",s+1);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号