[bzoj3991] [洛谷P3320] [SDOI2015] 寻宝游戏
Description
小B最近正在玩一个寻宝游戏,这个游戏的地图中有 \(N\) 个村庄和 \(N-1\) 条道路,并且任何两个村庄之间有且仅有一条路径可达。游戏开始时,玩家可以任意选择一个村庄,瞬间转移到这个村庄,然后可以任意在地图的道路上行走,若走到某个村庄中有宝物,则视为找到该村庄内的宝物,直到找到所有宝物并返回到最初转移到的村庄为止。小B 希望评测一下这个游戏的难度,因此他需要知道玩家找到所有宝物需要行走的最短路程。但是这个游戏中宝物经常变化,有时某个村庄中会突然出现宝物,有时某个村庄内的宝物会突然消失,因此小B需要不断地更新数据,但是小B太懒了,不愿意自己计算,因此他向你求助。为了简化问题,我们认为最开始时所有村庄内均没有宝物
Input
第一行,两个整数 \(N\) 、\(M\) ,其中 \(M\) 为宝物的变动次数。
接下来的 \(N-1\) 行,每行三个整数 \(x\)、\(y\)、\(z\),表示村庄 \(x\)、\(y\) 之间有一条长度为 \(z\) 的道路。
接下来的 \(M\) 行,每行一个整数 \(t\),表示一个宝物变动的操作。若该操作前村庄 \(t\) 内没有宝物,则操作后村庄内有宝物;若该操作前村庄 \(t\) 内有宝物,则操作后村庄内没有宝物。
Output
\(M\) 行,每行一个整数,其中第 \(i\) 行的整数表示第 \(i\) 次操作之后玩家找到所有宝物需要行走的最短路程。若只有一个村庄内有宝物,或者所有村庄内都没有宝物,则输出0。
Sample Input
4 5
1 2 30
2 3 50
2 4 60
2
3
4
2
1
Sample Output
0
100
220
220
280
HINT
\(1 \leq N \leq100000\)
\(1 \leq M \leq 100000\)
对于全部的数据,\(1 \leq z \leq10^9\)
想法
由于题目中要求找到所有宝物后要返回起点,故走过的每条路都走了2遍。
如果我们把所有有宝物的村庄(不妨称它们为关键节点)及它们的 \(lca\) 拎出来,单独建一棵树,我们要走的所有边便是这棵树上的所有边。
比如下图(蓝色的为关键节点):
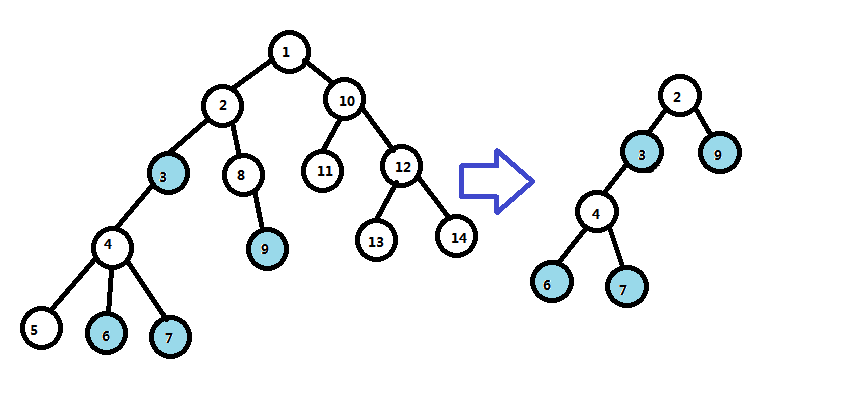
我们叫这棵树”虚树“。
让我们先回顾一下虚树的建树过程:
现在原树上 \(dfs\) 求出每个点的 \(dep\) 及 \(dfs序\)
然后将关键点按 \(dfs序\) 排序,依次考虑
用一个栈维护根到当前点 \(p\) 的路径
插入下一个点 \(q\) 时,根到 \(q\) 的路径中,\(q\) 的父节点为 \(lca(p,q)\)
于是就在原来根到 \(p\) 的路径中找合适的位置将 \(lca(p,q)\) (如果原路径中有就不用)及 \(q\) 插进去就行了。
这其中关键一步是“按 \(dfs序\) 排序”
而在这道题中,虚树的边数的二倍 便是按 \(dfs序\) 排序后的相邻的关键点之间的距离和(包括最后一个关键点与第一个关键点之间的距离)
(画个图就可理解了。。。每条边相当于在“进入”和“离开”时各经过一次)
那么我们只要对虚树中排序后所有相邻关键点求一遍距离,再加起来就行了。
但题目中还有修改,怎么办?
注意到每次修改只改一个点——如果这个点在虚树中,删掉它影响的只是虚树中与它相邻的两个关键点;如果不在虚树中,影响的也只是它插到虚树中后与它相邻的两个点。
于是我们可以用一个 \(set\) 来维护虚树中点的 \(dfs序\) ,每次修改只需在 \(set\) 中 \(O(logn)\) 寻找这个点的前驱后继。
如果要把这个点加到虚树中,\(ans\) 减去它相邻两个点之间的距离,加上它分别到相邻两个点的距离
如果要把这个点从虚树中删除,\(ans\) 减去它分别到相邻两个点的距离,加上它相邻两个点之间的距离
代码
一直用 \(set\) 不是很熟练
这次 \(get\) 了新技能:
y=*--st.lower_bound(x); //找小于x的最大数
z=*st.upper_bound(x); //找大于x的最小数
还有一个小技巧是在 \(set\) 中先加入 \(inf 与 -inf\) ,避免出现奇怪问题
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<set>
#define INF 1000000
using namespace std;
typedef long long ll;
const int N = 100005;
struct node{
int v,len;
node *next;
}pool[N*2],*h[N];
int cnt;
void addedge(int u,int v,int l){
node *p=&pool[++cnt],*q=&pool[++cnt];
p->v=v;p->next=h[u];h[u]=p;p->len=l;
q->v=u;q->next=h[v];h[v]=q;q->len=l;
}
int n,m,vis[N];
int f[N][20],dep[N],dfn[N],re[N],tot;
ll sum[N];
void dfs(int u){
int v;
dfn[u]=++tot; re[tot]=u;
for(node *p=h[u];p;p=p->next)
if(!dep[v=p->v]){
dep[v]=dep[u]+1;
f[v][0]=u; sum[v]=sum[u]+p->len;
for(int j=1;j<20;j++)
f[v][j]=f[f[v][j-1]][j-1];
dfs(v);
}
}
int lca(int x,int y){
if(dep[x]<dep[y]) swap(x,y);
for(int i=19;i>=0;i--)
if(dep[f[x][i]]>=dep[y]) x=f[x][i];
if(x==y) return x;
for(int i=19;i>=0;i--)
if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
return f[x][0];
}
inline ll Sum(int x,int y) { return sum[x]+sum[y]-sum[lca(x,y)]*2; }
set<int> st;
int main()
{
int x,y,z;
scanf("%d%d",&n,&m);
for(int i=1;i<n;i++){
scanf("%d%d%d",&x,&y,&z);
addedge(x,y,z);
}
dep[1]=1;
dfs(1);
int s,p,q;
ll t=0;
st.insert(-INF); st.insert(INF);
while(m--){
scanf("%d",&x);
if(vis[x]==0){
vis[x]=1;
s=st.size();
if(s==2) { st.insert(dfn[x]); printf("0\n"); continue; }
p=*--st.lower_bound(dfn[x]); q=*st.upper_bound(dfn[x]);
if(p==-INF) p=*--(--st.end());
if(q==INF) q=*++st.begin();
p=re[p]; q=re[q];
t=t-Sum(p,q)+Sum(p,x)+Sum(x,q);
st.insert(dfn[x]);
}
else{
vis[x]=0;
s=st.size();
if(s==2) { st.erase(dfn[x]); printf("0\n"); continue; }
p=*--st.lower_bound(dfn[x]); q=*st.upper_bound(dfn[x]);
if(p==-INF) p=*--(--st.end());
if(q==INF) q=*++st.begin();
p=re[p]; q=re[q];
t=t+Sum(p,q)-Sum(p,x)-Sum(x,q);
st.erase(dfn[x]);
}
printf("%lld\n",t);
}
return 0;
}

