[bzoj2115] [洛谷P4151] [Wc2011] Xor

Description###

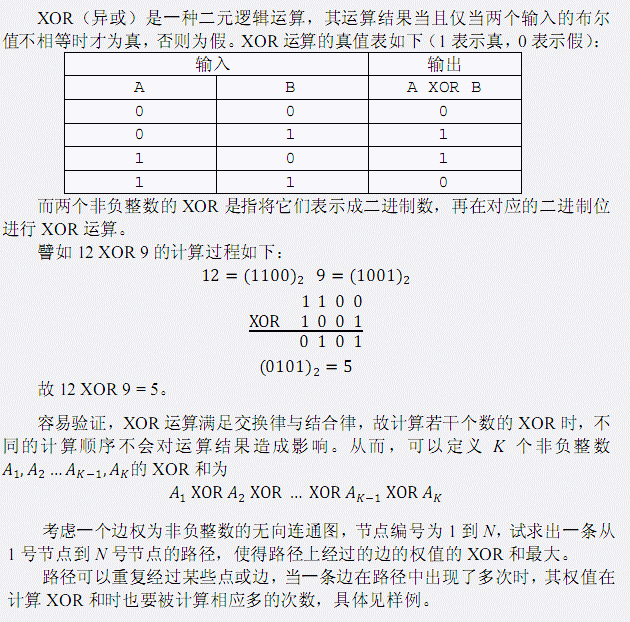
Input###

第一行包含两个整数N和 M， 表示该无向图中点的数目与边的数目。 接下来M 行描述 M 条边，每行三个整数Si，Ti ，Di，表示 Si 与Ti之间存在 一条权值为 Di的无向边。 图中可能有重边或自环。

Output###

仅包含一个整数，表示最大的XOR和（十进制结果）,注意输出后加换行回车。

Sample Input###

5 7

1 2 2

1 3 2

2 4 1

2 5 1

4 5 3

5 3 4

4 3 2

Sample Output###

6

HINT###

---

想法##

手动画画图后可以发现，最终对答案有贡献的边为一条从1到n的路径，及若干个环。
于是我们可以dfs一遍，找到所有的简单环及一条路径。
（为什么一条路径就可以呢？因为一条路径与某些 包括这路径上某些边的 环 异或起来，新的对答案有贡献的边会形成另一条路径。）
线性基维护每个简单环的异或和。
在已经选了的这个路径的异或和基础上，线性基中找出总异或和的max

---

代码##

#include<cstdio>
#include<iostream>
#include<algorithm>

using namespace std;

typedef long long ll;
const int N = 50005;

struct node{
    int v;
    ll len;
    node *next;	
}pool[N*4],*h[N];
int cnt;
void addedge(int u,int v,ll len){
    node *p=&pool[++cnt],*q=&pool[++cnt];
    p->v=v; p->next=h[u]; h[u]=p; p->len=len;
    q->v=u; q->next=h[v]; h[v]=q; q->len=len;
}

ll C[65];
void ins(ll x){
    if(!x) return;
    for(int i=63;i>=0;i--){
        if((x&(1ll<<i))==0) continue;
        if(!C[i]) { C[i]=x; return; }
        x^=C[i];
    }
}
ll cal(ll ret) { 
    for(int i=63;i>=0;i--) ret=max(ret,ret^C[i]);
    return ret;	
}

int vis[N];
ll d[N];
void dfs(int u){
    int v;
    vis[u]=1;
    for(node *p=h[u];p;p=p->next){
        v=p->v;
        if(!vis[v]){
            d[v]=d[u]^p->len;
            dfs(v);
        }
        else if(vis[v]==1)ins(d[u]^d[v]^p->len);
    }
    vis[u]=2;
}

int n,m;

int main()
{
    int u,v;
    ll len;
    scanf("%d%d",&n,&m);
    for(int i=0;i<m;i++){
        scanf("%d%d%lld",&u,&v,&len);
        addedge(u,v,len);	
    }
    
    dfs(1);
    printf("%lld\n",cal(d[n])); /*注意是在d[u]的基础上使异或和最大*/
    
    return 0;
}