《组合数学》学习笔记 之 二项式系数
5.1 帕斯卡三角形
换言之,杨辉三角。
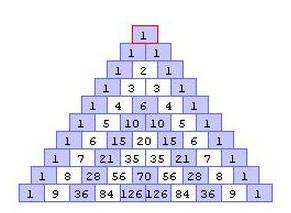
由其可发现3个性质:
1) \(\binom{n}{k}=\binom{n}{n-k}\)
2) \(\sum\limits_{k=0}^n \binom{n}{k}=2^n\)
3) 杨辉三角的项 \(\binom{n}{k}\) 的值代表从最上的点到这一项的路径数。
5.2 二项式定理
二项式定理
设 \(n\) 是正整数,对所有的 \(x\) 和 \(y\) 有 \((x+y)^n=\sum\limits_{k=0}^n \binom{n}{k} x^ky^{n-k}\)
在 \(y=1\) 时有特殊情形 : \((1+x)^n=\sum\limits_{k=0}^n \binom{n}{k} x^k\) ,也为常用公式。
关于二项式系数的常用恒等式:
1) \(k\binom{n}{k}=n\binom{n-1}{k-1}\)
将式子用定义打开即可证。
2) \(\binom{n}{0}+\binom{n}{1}+\binom{n}{2}+...+\binom{n}{n}=2^n\)
令 \(x=1,y=1\) ,代入二项式定理即可证。(也可组合推理)
3) 交错和 \(\binom{n}{0}-\binom{n}{1}+\binom{n}{2}-\binom{n}{3}+...+(-1)^n\binom{n}{n}=0\)
也可写成 \(\binom{n}{0}+\binom{n}{2}+...=\binom{n}{1}+\binom{n}{3}+...=2^{n-1}\)
令 \(x=1,y=-1\) ,代入二项式定理即可证。(也可组合推理)
4) \(1\binom{n}{1}+2\binom{n}{2}+...+n\binom{n}{0}=n2^{n-1}\)
利用 \(k\binom{n}{k}=n\binom{n-1}{k-1}\) ,左式可写成 \(n\binom{n-1}{0}+n\binom{n-1}{1}+...+n\binom{n-1}{n-1}=n2^{n-1}\)。
5) 利用连续求导及关于 \(x\) 的乘法得到 \(\sum\limits_{k=1}^n k^p\binom{n}{k}\) 关于正整数 \(p\) 的恒等式
由 \((1+x)^n=\sum\limits_{k=0}^n \binom{n}{k} x^k\)
两边对 \(x\) 求导 : \(n(1+x)^{n-1}=\sum\limits_{k=0}^n \binom{n}{k} kx^{k-1}\)
(令 \(x=1\) 可得 : \(n2^{n-1}=\sum\limits_{k=0}^n k\binom{n}{k}=\sum\limits_{k=1}^n k\binom{n}{k}\) )
两边同乘 \(x\) 得 : \(nx(1+x)^{n-1}=\sum\limits_{k=0}^n \binom{n}{k} kx^k\)
两边对 \(x\) 求导 : \(n((1+x)^{n-1}+x(n-1)(1+x)^{n-2})=\sum\limits_{k=0}^n \binom{n}{k} k^2x^{k-1}\)
(令 \(x=1\) 可得 : \(n(n+1)2^{n-2}=\sum\limits_{k=0}^n k^2\binom{n}{k}=\sum\limits_{k=1}^n k^2\binom{n}{k}\) )
6) 范德蒙卷积公式 \(\sum\limits_{k=0}^n \binom{m1}{k}\binom{m2}{n-k}=\binom{m1+m2}{n}\)
特殊形式 \(\sum\limits_{k=0}^n \binom{n}{k}^2=\binom{2n}{n}\)
利用组合推理证明:
设 \(S\) 为拥有 \(m1+m2\) 个元素的集合,则 \(\binom{m1+m2}{n}\) 计数的是 \(S\) 的 \(n\) 元子集的数目。
把 \(S\) 划分为 \(A,B\) 两个子集,其中 \(|A|=m1,|B|=m2\)。
考虑每个 \(S\) 的 \(n\) 元子集,其包含 \(k\) 个 \(A\) 元素和 \(n-k\) 个 \(B\) 元素,\(k\) 为 \(0\) 到 \(n\) 之间的整数。
则 \(S\) 的 \(n\) 元子集可根据 \(k\) 的大小划分为 \(n+1\) 个部分,而每部分的大小为 \(\binom{m1}{k}\binom{m2}{n-k}\)
由加法原理可得,\(\sum\limits_{k=0}^n \binom{m1}{k}\binom{m2}{n-k}=\binom{m1+m2}{n}\)
广义二项式系数
\(\binom{r}{k}\) ,\(r\in R,k\in Z\)
公式 \(\binom{r}{k}=\binom{r-1}{k}+\binom{r-1}{k-1}\) 与 \(k\binom{r}{k}=r\binom{r-1}{k-1}\) 仍成立。
可由帕斯卡公式递推得到两个求和公式:
1) \(\binom{r}{0}+\binom{r+1}{1}+..\binom{r+k}{k}=\binom{r+k+1}{k}\)
在左式首加 \(\binom{r}{-1}\) 即可证。
2) \(\binom{0}{k}+\binom{1}{k}+..\binom{n}{k}=\binom{n+1}{k+1}\)
在左式首加 \(\binom{0}{k+1}\) 即可证。
5.3 二项式系数的单峰性
二项式系数序列 \(\binom{n}{0},\binom{n}{1},...,\binom{n}{n}\) 为单峰序列,最大者为 \(\binom{n}{\lfloor n/2 \rfloor}=\binom{n}{\lceil n/2 \rceil}\)
5.4 多项式定理
符号太难打了,略……
5.5 牛顿二项式定理

几个导出式在生成函数中很重要。
5.6 再论偏序集
定理5.6.1 (\(Dilworth\) 定理的“对偶”定理)
设(\(X,\leq\)) 为有限偏序集,设 \(r\) 为链的最大大小。则 \(X\) 可被划分成 \(r\) 条反链,不可划分成小于 \(r\) 条反链。
\(Dilworth\) 定理
设(\(X,\leq\)) 为有限偏序集,设 \(m\) 为反链的最大大小。则 \(X\) 可被划分成 \(m\) 条链,不可划分成小于 \(m\) 条链。

