【复习】图论

 

一、并查集

1、普通并查集

 

inline int father(int x)
{
	if(fath[x]==x) return x;
	return fath[x]=father(fath[x]);
}

inline void Union(int x,int y)
{
	int f1=father(x),f2=father(y);
	if(f1==f2) return;
	fath[f1]=f2;
}

 

 

2、带权并查集

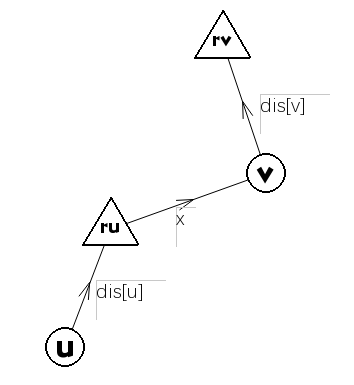
如图，$dis[u]$表示$u$到$root-u$的距离，此时要合并两颗树，则以$root-v$为新根，$dis[ru]=Relationship(u,v)+dis[v]-dis[u]$。

当路径压缩时，$dis[x]+=dis[fath[x]]$。

此时有个重点，假如关系类型种类为$P$，所有$dis$要模$P$，关系种类满足递增性，循环性，可理解为$P$个一循环。

重点例题: [HNOI2005]狡猾的商人 (多种关系), Rochambeau (三种关系) , True Liars (两种关系)，食物链 (三种关系)

 

inline int father(int x)
{
	if(fath[x]==x) return x;
	int fa=father(fath[x]);
	dis[x]=(dis[x]+dis[fath[x]])%P;
	return fath[x]=fa;
}

inline void Union(int x,int y,int rela)
{
	int f1=father(x),f2=father(y);
	if(f1==f2) return;
	dis[f2]=(rela+dis[x]-dis[y]+P)%P;
	fath[f2]=f1;
}

 

二、联通分量（$O(n+m)$）

1、强连通分量

inline void Tarjan(int x)
{
	st.push(x);
	vis[x]=1;
	low[x]=dfn[x]=++idx;
	for(int i=head[x];i;i=edge[i].nxt)
	{
		int v=edge[i].to;
		if(!dfn[v])
		{
			Tarjan(v);
			low[x]=min(low[v],low[x]);
		}
		else if(vis[v]) low[x]=min(low[x],dfn[v]);
	}
	if(low[x]==dfn[x])
	{
		int now=0;
		ncon++;
		while(now!=x)
		{
			now=st.top();
			st.pop();
			col[now]=ncon;
			vis[now]=0;
		}
	}
}

 

2、边双联通分量（只加一个fa）

inline void Tarjan(int x,int fa)
{
	st.push(x);
	vis[x]=1;
	low[x]=dfn[x]=++idx;
	for(int i=head[x];i;i=edge[i].nxt)
	{
		int v=edge[i].to;
		if(!dfn[v])
		{
			Tarjan(v,x);
			low[x]=min(low[v],low[x]);
		}
		else if(vis[v] && v!=fa) low[x]=min(low[x],dfn[v]);
	}
	if(low[x]==dfn[x])
	{
		int now=0;
		ncon++;
		while(now!=x)
		{
			now=st.top();
			st.pop();
			col[now]=ncon;
			new_val[ncon]+=val[now];
			vis[now]=0;
		}
	}
}

 

3、点双联通分量

不含桥，环与环必定含有公共边，且公共点至少两个，简单圈中的点一定属于同一个点BCC：

inline void Tarjan(int x,int fa)
{
	st.push(x);
	low[x]=dfn[x]=++idx;
	vis[x]=1;
	for(int i=head[x];i;i=edge[i].nxt)
	{
		int v=edge[i].to;
		if(!dfn[v])
		{
			Tarjan(v,fa);
			if(low[v]<low[x]) low[x]=low[v];
			else if(low[v]>=low[x]) 
			{
				ncon++;
				int now=0;
				while(1)
				{
					now=st.top();
					st.pop();
			 		col[now]=ncon;
					vis[now]=0;
					if(now==v) break;
				}
				col[x]=ncon;
			}
		}
		else if(vis[v]) low[x]=min(low[x],dfn[v]);
	}
}

　　

4、桥

inline void Tarjan(int x,int fa)
{
	low[x]=dfn[x]=++idx;
	for(int i=head[x];i;i=edge[i].nxt)
	{
		int v=edge[i].to;
		if(!dfn[v])
		{
			Tarjan(v,x);
			low[x]=min(low[x],low[v]);
			if(low[v]>low[x]) bri.push(mp(x,v));
		}
		else if(v!=fa) low[x]=min(low[x],dfn[v]);
	}
}

 

5、割点

inline void Tarjan(int x,int fa)
{
	int child=0;
	low[x]=dfn[x]=++idx;
	for(int i=head[x];i;i=edge[i].nxt)
	{
		int v=edge[i].to;
		if(!dfn[v])
		{
			Tarjan(v,x);
			low[x]=min(low[x],low[v]);
			if(low[v]>=dfn[x]) cut[x]=1;
			child++;
		}
		else if(v!=fa) low[x]=min(low[x],dfn[v]);
	}
	if(child==1 && fa==0) cut[x]=0;
}

 

6、2-sat

输出方案，对于每个对立的问题，选择BCC编号小的那个。