CF999E Reachability from the Capital

1、处理以$s$开头的联通块

2、处理以入度为零的点开头的联通块

3、处理环的联通块，此时要注意，有可能出现环串，所以要允许标号覆盖，否则会多记，因为是环的缘故，无法像2那样一次做到从头处理。就是下面这种情况（2,3,4都是环的标号）

 

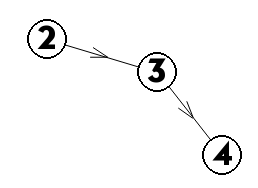
但是无论如何，1所在的环都只能从1遍历到，所以1所在的环不能被覆盖，所有指向1的边干脆不要建。

CODE:

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <set>
using namespace std;
const int maxn=5005;
struct point
{
	int to;
	int nxt;
}edge[maxn];
int n,tot,m,s,cnt;
int head[maxn];
int in[maxn],vis[maxn];
set<int> S;


inline void add(int u,int v)
{
	tot++;
	edge[tot].nxt=head[u];
	edge[tot].to=v;
	head[u]=tot;
}

inline void dfs(int x)
{
	vis[x]=cnt;
	for(int i=head[x];i;i=edge[i].nxt)
	{
		int v=edge[i].to;
		if(vis[v]==cnt || v==s) continue;
		dfs(v);
	}
}

int main()
{
	scanf("%d%d%d",&n,&m,&s);
	for(int i=1;i<=m;i++)
	{
		int u,v;
		scanf("%d%d",&u,&v);
		add(u,v);
		in[v]++;
	}
	cnt=1;
	dfs(s); 
	for(int i=1;i<=n;i++)
		if(!vis[i] && in[i]==0)
		{
			cnt++;
			dfs(i);
			
		}
	for(int i=1;i<=n;i++)
		if(!vis[i]) 
		{
			cnt++;
			dfs(i);
			
		}
	for(int i=1;i<=n;i++) S.insert(vis[i]);
	printf("%d",S.size()-1);
	return 0;
}