【复习】关于莫比乌斯

 

一、 $\mu$的基本定义

 $\mu(x)=$$\begin{cases}1\ \ \ \ \ (x=1)\\0\ \ \ \ \  (x有平方因子)\\-1\ \ (x有奇数个质因子)\\1\ \ (x有偶数数个质因子) \end{cases}$

 

二、相关性质

1、莫比乌斯反演常用：

$$\sum_{d|n}\mu(d)=[n=1]$$

2、把欧拉函数和莫比乌斯函数结合起来：

$$\sum_{d|n}\frac{\mu(d)}{d}=\frac{\varphi(n)}{n}$$

 

三、莫比乌斯反演

1、倍数莫比乌斯反演：

若：$f(n)=\sum_{n|d}g(d)$
则：$g(n)=\sum_{n|d}\mu(\frac{d}{n})f(d)$

2、约数莫比乌斯反演：

若：$f(n)=\sum_{d|n}g(d)$
则：$g(n)=\sum_{d|n}\mu(d)f(\frac{n}{d})$

 

四、求$\mu$

1、线性筛

void get_miu()
{
	miu[1]=1;
	for(int i=2;i<maxn;i++)
	{
		if(!mark[i])
		{
			p[++p[0]]=i;
			miu[i]=-1;
		}
		for(int j=1;j<=p[0] && i*p[j]<maxn;j++)
		{
			mark[i*p[j]]=1;
			if(i%p[j]==0)
			{
				miu[i*p[j]]=0;
				break;
			}
			else miu[i*p[j]]=-miu[i];
		}
	}
}

2、杜教筛求前缀和

 

 

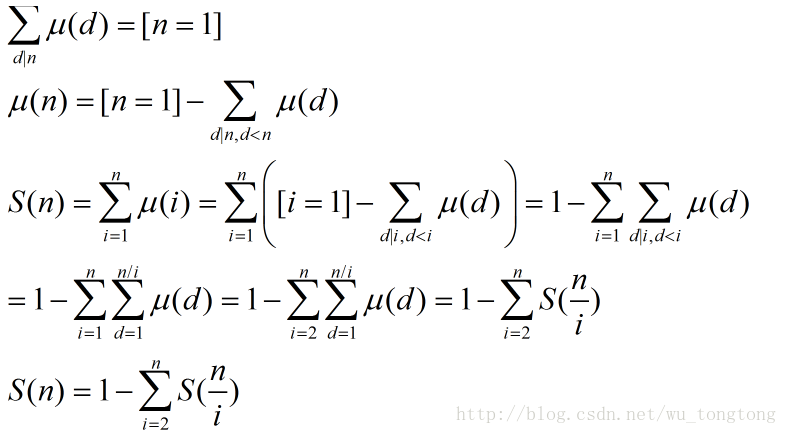
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <map> 
typedef long long ll;
using namespace std;
const int maxn=5e6+10;
ll a,b;
int miu[maxn],tot;
map<ll,ll> mp;

bool mark[maxn];
int p[maxn];

void init()
{
	miu[1]=1;
	for(int i=2;i<maxn;i++)
	{
		if(!mark[i])
		{
			p[++p[0]]=i;
			miu[i]=-1;
		}
		for(int j=1;j<=p[0] && i*p[j]<maxn;j++)
		{
			mark[i*p[j]]=1;
			if(i%p[j]==0)
			{
				miu[i*p[j]]=0;
				break;
			}
			else miu[i*p[j]]=-miu[i];
		}
	}
	for(int i=1;i<maxn;i++) miu[i]+=miu[i-1];
}

ll sum(ll x)
{
	if(x<maxn) return miu[x];
	if(mp.count(x)) return mp[x]; 
	ll r=0,res=1;
	for(long long i=2;i<=x;i=r+1)
	{
		r=x/(x/i);
		res-=sum(x/i)*(r-i+1);
	}
	return mp[x]=res; 
}

int main()
{
	init();
	scanf("%lld%lld",&a,&b);
	printf("%lld\n",sum(b)-sum(a-1));	
	return 0;
}