NOI 2012

[NOI2012]随机数生成器

矩阵乘法，要注意两数相乘时，可能会爆long long，用快速乘。

 

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
long long mod1,a,c,x,n,mod2;

long long mul(long long p,long long b)
{
    long long res=0;
    for(;b;b>>=1)
    {
        if(b&1) res=(res+p)%mod1;
        p=(p+p)%mod1;
    }
    return res;
}

struct Matrix
{
    long long a[10][10];
    Matrix(){memset(a,0,sizeof(a));}
    Matrix operator * (const Matrix &aa)
    {
        Matrix c;
        for(int i=1;i<=9;i++)
            for(int j=1;j<=9;j++)
                for(int p=1;p<=9;p++)
                    c.a[i][j]=(c.a[i][j]%mod1+mul((a[i][p]%mod1),(aa.a[p][j]%mod1))%mod1)%mod1;
        return c;
    }
};

Matrix Pow(Matrix p,long long b)
{
    Matrix res;
    for(int i=1;i<=3;i++) res.a[i][i]=1LL;
    for(;b;b>>=1)
    {
        if(b&1) res=res*p;
        p=p*p;
    }
    return res;
}

int main()
{
    scanf("%lld%lld%lld%lld%lld%lld",&mod1,&a,&c,&x,&n,&mod2);
    Matrix trans,ini;
    trans.a[1][1]=0,trans.a[1][2]=0,trans.a[1][3]=0;
    trans.a[2][1]=1,trans.a[2][2]=a%mod1,trans.a[2][3]=0;
    trans.a[3][1]=0,trans.a[3][2]=1,trans.a[3][3]=1;
    ini.a[1][1]=0,ini.a[1][2]=x,ini.a[1][3]=c%mod1;
    Matrix ans=ini*Pow(trans,n);
    printf("%lld",(ans.a[1][2]%mod2+mod2)%mod2);
    return 0;
}

 

 

[NOI2012]美食节

本来应该这样建图，把每个厨师拆成sigma_p个点，分别表示倒数第i次做菜的该位厨师j，向每个菜品p连边。

但是这样会TLE，我们不妨模拟一下MCMF的过程，对于每个厨师来说，首先SPFA出来的代价最小的通路肯定是最后一次做某菜，因为等待的时间短。我们不妨先建所有的倒数第一个点，哪个满流了就建倒数第二个点，很好的模拟了增广的过程，剪掉了许多不必要的边。

CODE:

 

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int maxm=1e7+10;
const int maxn=1e5+10;
#define idd(i,j) ((i-1)*sum+j+n)
#define left(x) ((x-n-1)/sum+1)
#define right(x) ((x-n-1)%sum+1)
struct point
{
    int to,nxt;
    int cap,cost;
}edge[maxm];
int n,m,Mincost,Maxflow,tot,S,T,sum;
int head[maxn],p[maxn],flow[maxn],vis[maxn],id[maxn],pre[maxn],dis[maxn];
int ti[120][120];

inline void add(int u,int v,int c,int f)
{
    edge[tot]=(point){v,head[u],c,f};
    head[u]=tot++;
    edge[tot]=(point){u,head[v],0,-f};
    head[v]=tot++;
}

inline bool Bfs()
{
    queue<int> q;
    memset(dis,-1,sizeof(dis));
    memset(vis,0,sizeof(vis));
    dis[S]=0; flow[S]=1e9; vis[S]=1;
    q.push(S);
    while(!q.empty())
    {
        int tt=q.front();
        q.pop();
        vis[tt]=0;
        for(int i=head[tt];~i;i=edge[i].nxt)    
        {
            int v=edge[i].to;
            if(edge[i].cap && (dis[v]==-1 || dis[v]>dis[tt]+edge[i].cost))
            {
                dis[v]=dis[tt]+edge[i].cost;
                flow[v]=min(edge[i].cap,flow[tt]);
                id[v]=i; pre[v]=tt;
                if(!vis[v]) vis[v]=1,q.push(v);
            }
        }
    }    
    return dis[T]!=-1;
}

inline void Mcmf()
{
    while(Bfs())
    {
        int tmp=T,ad=0;
        while(tmp!=S)
        {
            edge[id[tmp]].cap-=flow[T];
            edge[id[tmp]^1].cap+=flow[T];
            tmp=pre[tmp];
        }
        Mincost+=flow[T]*dis[T];
        ad=pre[T]+1;
        add(ad,T,1,0);
        for(int i=1;i<=n;i++)
            add(i,ad,1,ti[i][left(ad)]*right(ad));
    }
}

int main()
{
    memset(head,-1,sizeof(head));
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        scanf("%d",&p[i]),sum+=p[i];
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            scanf("%d",&ti[i][j]);
    S=0,T=sum*m+n+1;
    for(int i=1;i<=n;i++) add(S,i,p[i],0);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            add(i,idd(j,1),1,ti[i][j]);
    for(int i=1;i<=m;i++)
        add(idd(i,1),T,1,0);
    Mcmf();
    printf("%d",Mincost);
    return 0;
}

 

　　

 

 

[NOI2012]迷失游乐园

当只有树的时候很套路，up[x]表示从节点x向上走的期望长度，down[x]表示从节点x向下走的期望长度。

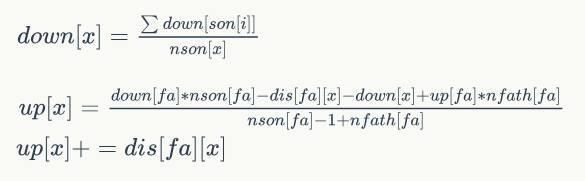
当是基环树的时候，先算down[x]，每棵树的树根的up[x]要注意一下，左右全部跑一遍，对于每个环内的点都有可能继续走或下到树里面。

CODE:

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn=1e5+10;
struct point
{
    int to;
    int nxt;
    double w;
}edge[maxn*2];
int n,m,tot,cnt,flag;
double up[maxn],down[maxn],w_fa[maxn],W[33][33];
int hav[maxn],nson[maxn],head[maxn],nn[33],in[maxn],vis[maxn],hash[maxn];
int fath[maxn],pre[maxn],nex[maxn];
 
inline void add(int u,int v,double w)
{
    tot++;
    edge[tot].nxt=head[u];
    edge[tot].to=v;
    edge[tot].w=w;
    head[u]=tot;
}
 
inline void dfs1(int x,int fa)
{
    for(int i=head[x];i;i=edge[i].nxt)
    {
        int v=edge[i].to;
        if(vis[v] || v==fa) continue;
        nson[x]++,w_fa[v]=edge[i].w;
        hav[v]=1;
        dfs1(v,x);
        down[x]+=down[v]+(double)edge[i].w;
    }
    if(nson[x]) down[x]/=(double)nson[x];
}
 
inline void dfs2(int x,int fa)
{
    if(fa)
    {
        if(nson[fa]-1+hav[fa]>0)
            up[x]=(double)(down[fa]*nson[fa]-w_fa[x]-down[x]+hav[fa]*up[fa])/(double)(nson[fa]-1+hav[fa]);
        up[x]+=(double)w_fa[x];
    }
    for(int i=head[x];i;i=edge[i].nxt)
    {
        int v=edge[i].to;
        if(vis[v] || v==fa) continue;
        dfs2(v,x);
    }
}
 
inline void Tree_solve()
{
    dfs1(1,0);
    dfs2(1,0);
}
 
inline void get_cir(int x,int fa)
{
    vis[x]=1;
    for(int i=head[x];i;i=edge[i].nxt)
    {
        int v=edge[i].to;
        if(v==fa) continue;
        if(vis[v]){flag=v; return;}
        get_cir(v,x);
        if(flag>0){if(flag==x) flag=-1; return;}
        if(flag==-1) break;
    }
    vis[x]=0;
}
 
void find_cir(int x, int f)
{
    if(hash[x]) return;
    nn[++cnt] = x;
    hash[x] = cnt;
    hav[x]=2;
    for(int i=head[x];i;i=edge[i].nxt)
    {
        int v=edge[i].to;
        if (v == f) continue;
        if (!vis[v]) continue;
        pre[v] = x; nex[x] = v;
        find_cir(v, x);
        W[hash[x]][hash[v]] = W[hash[v]][hash[x]] = edge[i].w;
        break;
    }
}
 
inline void Cir_Tree_solve()
{
    for(int i=1;i<=n;i++) if(vis[i])
    {
        find_cir(i,0);
        break;   
    }
    double nowp;
    memset(w_fa,0,sizeof(w_fa));
    for(int i=1;i<=cnt;i++) dfs1(nn[i],0);
    for (int i=1;i<=cnt;i++)
    {
        double k=1.0;
        int u=nn[i];
        for(int j=nex[u];j!=u;j=nex[j])
        {
            if(nex[j]!=u) up[u]+=(double)k*((down[j]*nson[j])/(double)(nson[j]+1)+W[hash[pre[j]]][hash[j]]);
            else up[u]+=k*(down[j]+W[hash[pre[j]]][hash[j]]);
            k/=(nson[j]+1);
        }
        k=1.0;
        for(int j=pre[u];j!=u;j=pre[j])
        {
            if(pre[j]!=u) up[u]+=(double)k*((down[j]*nson[j])/(double)(nson[j]+1)+W[hash[nex[j]]][hash[j]]);
            else up[u]+=k*(down[j]+W[hash[nex[j]]][hash[j]]);
            k/=(nson[j]+1);
        }
        up[u]/=2.0;
    }
    for(int i=1;i<=cnt;i++) dfs2(nn[i],0);
}
 
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)
    {
        int u,v;
        double w;
        scanf("%d%d%lf",&u,&v,&w);
        add(u,v,w),add(v,u,w);
    }
    get_cir(1,0);
    if(m<=n-1) Tree_solve();
    else Cir_Tree_solve();
    double ans=0.0;
    for(int i=1;i<=n;i++)
        ans=ans+(up[i]*hav[i]+down[i]*nson[i])/(double)(nson[i]+hav[i]);
    ans/=(double)n;
    printf("%.5lf",ans);
    return 0;
}

　　

 

 

[NOI2012]骑行川藏

讲的很清楚。

CODE:

 

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define eps 1e-12
const int maxn=1e4+10;
const int inf=1e9;
int n;
double E,s[maxn],k[maxn],v[maxn],x[maxn];

inline double cal(double lam)
{
    double tmp=0;
    for(int i=1;i<=n;i++)
    {
        double l=max(0.0,v[i]),r=inf;
        while(l+eps<r)
        {
            double mid=(l+r)*0.5;
            if(2*lam*k[i]*mid*mid*(mid-v[i])>1)
                r=mid;
            else l=mid;
        }
        x[i]=(l+r)*0.5;
        tmp+=k[i]*(x[i]-v[i])*(x[i]-v[i])*s[i];
    }
    return tmp;
}

int main()
{
    scanf("%d%lf",&n,&E);
    for(int i=1;i<=n;i++)
        scanf("%lf%lf%lf",&s[i],&k[i],&v[i]);
    double l=0,r=inf;
    while(l+eps<r)
    {
        double mid=(l+r)*0.5;
        if(cal(mid)>=E) l=mid;
        else r=mid;
    }
    double ans=0;
    for(int i=1;i<=n;i++)
        ans+=s[i]/x[i];
    printf("%.10lf",ans);
    return 0;
}