NOI 2010
[NOI2010]能量采集
暴力80,不说话/

CODE:

#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> using namespace std; const int maxn=1e5+10; int n,m; long long ans,f[maxn]; int main() { scanf("%d%d",&n,&m); int Max=min(m,n); for(int i=Max;i>=1;i--) { f[i]=(long long)(n/i)*(m/i); for(int j=2;j*i<=Max;j++) f[i]-=f[i*j]; ans+=f[i]*(i+i-1); } printf("%lld\n",ans); return 0; }
[NOI2010]航空管制
先建图
1、输出方案很simple,拓扑排序后贪心地选择 t 值最小的先起飞,题目保证有解。
2、第二问反向建图,贪心地让每架飞机尽量最晚被加入队列,在实在没有合法的起飞飞机的时候就是每架飞机在反图中的最晚时间。
CODE:

#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> #define MP(a,b) make_pair(a,b) using namespace std; const int maxn=20003; struct point { int to; int nxt; }edge[maxn*2]; int n,m,tot; int head[maxn],t[maxn],IN[maxn],in[maxn],ans1[maxn],nn; typedef pair<int,int> mp; priority_queue<mp> q; inline void add(int u,int v) { tot++; edge[tot].nxt=head[u]; edge[tot].to=v; head[u]=tot; } inline int ask(int x) { while(!q.empty()) q.pop(); memcpy(IN,in,sizeof(in)); IN[x]=n; for(int i=1;i<=n;i++) if(!IN[i]) q.push(MP(t[i],i)); for(int i=n;i>=1;i--) { if(q.empty() || q.top().first<i) return i; int tt=q.top().second;q.pop(); for(int j=head[tt];j;j=edge[j].nxt) { int v=edge[j].to; IN[v]--; if(!IN[v]) q.push(MP(t[v],v)); } } printf("OKKK\n"); } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) scanf("%d",&t[i]); for(int i=1;i<=m;i++) { int u,v; scanf("%d%d",&u,&v); add(v,u); in[u]++; } memcpy(IN,in,sizeof(in)); for(int i=1;i<=n;i++) if(IN[i]==0) q.push(MP(t[i],i)); while(!q.empty()) { int x=q.top().second; ans1[++nn]=x; q.pop(); for(int i=head[x];i;i=edge[i].nxt) { int v=edge[i].to; IN[v]--; if(!IN[v]) q.push(MP(t[v],v)); } } for(int i=nn;i>=1;i--) printf("%d ",ans1[i]); printf("\n"); for(int i=1;i<=n;i++) printf("%d ",ask(i)); return 0; }
[NOI2010]海拔
贪心地想,一定是只有0和1的,因为网格中已经给了一个0一个1,再想想,0和1应当各自连成一片,那么就很simple了,贡献只会在0和1分界处。
既然要求贡献最小,那么就是最小割了。(直接Dinic会TLE)
平面图最小割—>最大流—>对偶图最短路
对偶图就是这样:
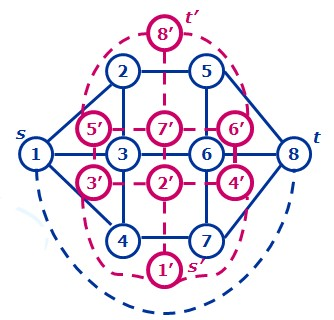
相当于把每个格子看成点,新建图的每条边对应了原图某条边的割,因此对偶图边数=原图边数
CODE:

#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> #define MP(a,b) make_pair(a,b) using namespace std; const int maxn=2600000; struct point { int to; int nxt; long long w; }edge[maxn*2]; int n,w,S,T,tot; int head[maxn],vis[maxn]; long long dis[maxn]; priority_queue<pair<long long,int> > q; inline void Dij() { memset(dis,0x3f,sizeof(dis)); memset(vis,0,sizeof(vis)); dis[S]=0; vis[S]=1; q.push(MP(0,S)); while(!q.empty()) { int tt=q.top().second; q.pop(); vis[tt]=0; for(int i=head[tt];i;i=edge[i].nxt) { int v=edge[i].to; if(dis[v]>dis[tt]+edge[i].w) { dis[v]=dis[tt]+edge[i].w; if(!vis[v]) vis[v]=1,q.push(MP(-dis[v],v)); } } } } inline void add(int u,int v,long long w) { tot++; edge[tot].nxt=head[u]; edge[tot].to=v; edge[tot].w=w; head[u]=tot; } inline int pos(int x,int y) { if(x==0 || y==n+1) return S; if(x==n+1 || y==0) return T; return (x-1)*n+y; } int main() { scanf("%d",&n); S=n*n+3,T=S+1; long long x; for(int i=0;i<=n;i++) for(int j=1;j<=n;j++) { scanf("%lld",&x); add(pos(i,j),pos(i+1,j),x); } for(int i=1;i<=n;i++) for(int j=0;j<=n;j++) { scanf("%lld",&x); add(pos(i,j+1),pos(i,j),x); } for(int i=0;i<=n;i++) for(int j=1;j<=n;j++) { scanf("%lld",&x); add(pos(i+1,j),pos(i,j),x); } for(int i=1;i<=n;i++) for(int j=0;j<=n;j++) { scanf("%lld",&x); add(pos(i,j),pos(i,j+1),x); } Dij(); printf("%lld",dis[T]); return 0; }
[NOI2010]超级钢琴
预处理了前缀和后,一段区间和相当于是一个数对,而对于一个右端点来说,合法的左端点一定是一段区间(查询的时候ST表RMQ),我们可以优先队列存储这些数对和值,但是不可能真的存储一个个数对,一定是( [l , r] , R)这样的结构,那问题就来了,当我们查询了[l , r]的min后,如何删掉min呢?
我们发现,加入原来x的左端点可以在[a,b]中选择,我们与其从[a,b]中去掉y,不如将[a,b]分裂成[a,y-1]和[y+1,b]两段,然后将这两段都扔到优先队列中。也就是说,我们在优先队列中存放的其实是一个四元组(sum,x,a,b),分别代表区间和,右端点,合法左端点的区间最左边和最右边。
CODE:

#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> #define mp(a,b,c,d) make_pair(make_pair(a,b),make_pair(c,d)) using namespace std; const int maxn=5e5+10; int n,k,L,R; int f[maxn][20],Log[maxn]; typedef pair<int,int> pii; priority_queue<pair<pii,pii> > q; long long s[maxn]; inline int Min(int i,int j) { return s[i]<s[j]?i:j; } inline int query(int l,int r) { if(l>r) return -1; int kk=Log[r-l+1]; return Min(f[l][kk],f[r-(1<<kk)+1][kk]); } int main() { scanf("%d%d%d%d",&n,&k,&L,&R); for(int i=2;i<=n;i++) Log[i]=Log[i>>1]+1; for(int i=1;i<=n;i++) scanf("%lld",&s[i]),s[i]+=s[i-1],f[i][0]=i; for(int j=1;(1<<j)<=n;j++) for(int i=0;i+(1<<j)-1<=n;i++) f[i][j]=Min(f[i][j-1],f[i+(1<<j-1)][j-1]); for(int i=L;i<=n;i++) { int kj=query(max(0,i-R),i-L); long long mn=s[kj]; q.push(mp(s[i]-mn,i,max(0,i-R),i-L)); } long long ans=0; while(k--) { pii aa=q.top().first,bb=q.top().second; q.pop(); int l=bb.first,r=bb.second,ii=aa.second; ans+=aa.first; int yy=query(l,r); int ll=query(l,yy-1),rr=query(yy+1,r); if(ll!=-1) q.push(mp(s[ii]-s[ll],ii,l,yy-1)); if(rr!=-1) q.push(mp(s[ii]-s[rr],ii,yy+1,r)); } printf("%lld",ans); return 0; }
[NOI2010]旅行路线
这题n<=3,搜索就可以拿到60(听说是70??),但要加一个优化,因为最后所有的格子都要走,所以如果某一列全部走了但是左右两边的部分均有未走的格子,就不可能走完,return掉。
正解是插头DP?
CODE:

#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> using namespace std; const int mod=11192869; int map[5][404],mark[20010]; int n,m,vis[2002][2002]; long long ans; char ss[304]; int derx[]={0,0,0,1,-1}; int dery[]={0,1,-1,0,0}; inline long long read() { long long Sum=0; char ch=getchar(); while(ch<'0' || ch>'9') {ch=getchar();} while(ch>='0' && ch<='9') {Sum=Sum*10+ch-'0'; ch=getchar();} return Sum; } inline bool check(int x,int y) { int f1=1,f2=1; for(int i=1;i<=n;i++) for(int j=1;j<y;j++) if(!vis[i][j]) { f1=0; break; } for(int i=1;i<=n;i++) for(int j=y+1;j<=m;j++) if(!vis[i][j]) { f2=0; break; } if(f1==0 && f2==0) return false; return true; } inline void dfs(int x,int y,int dep) { if(x==1 || x==n) { if(x==1) { if(n==2 && vis[x+1][y] && !check(x,y)) return; if(n==3 && vis[x+1][y] && vis[x+2][y] && !check(x,y)) return; } else { if(n==2 && vis[x-1][y] && !check(x,y)) return; if(n==3 && vis[x-1][y] && vis[x-2][y] && !check(x,y)) return; } } vis[x][y]=1; if(dep==n*m) { vis[x][y]=0; ans=(ans+1)%mod; return; } int xx,yy; for(int i=1;i<=4;i++) { xx=x+derx[i],yy=y+dery[i]; if(xx<1 || xx>n || yy<1 || yy>m) continue; if(vis[xx][yy] || map[xx][yy]!=mark[dep+1]) continue; dfs(xx,yy,dep+1); } vis[x][y]=0; } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) if(read()) map[i][j]=1; } for(int i=1;i<=n*m;i++) if(read()) mark[i]=1; for(int i=1;i<m;i++) if(map[1][i]==mark[1]) dfs(1,i,1); for(int i=1;i<n;i++) if(map[i][m]==mark[1]) dfs(i,m,1); for(int i=2;i<=m;i++) if(map[n][i]==mark[1]) dfs(n,i,1); for(int i=2;i<=n;i++) if(map[i][1]==mark[1]) dfs(i,1,1); printf("%lld",ans); return 0; }



