USACO 4.3 街道赛跑 【推理+深搜】

题目

图一表示一次街道赛跑的跑道。可以看出有一些路口（用 0 到 N 的整数标号），和连接这些路口的箭头。路口 0 是跑道的起点，路口 N 是跑道的终点。箭头表示单行道。运动员们可以顺着街道从一个路口移动到另一个路口（只能按照箭头所指的方向）。当运动员处于路口位置时，他可以选择任意一条由这个路口引出的街道。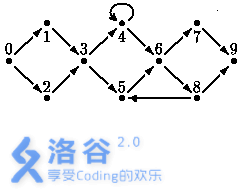

图一：有 10 个路口的街道
一个良好的跑道具有如下几个特点：
每一个路口都可以由起点到达。
从任意一个路口都可以到达终点。
终点不通往任何路口。
运动员不必经过所有的路口来完成比赛。有些路口却是选择任意一条路线都必须到达的（称为“不可避免”的）。在上面的例子中，这些路口是 0，3，6，9。对于给出的良好的跑道，你的程序要确定“不可避免”的路口的集合，不包括起点和终点。
假设比赛要分两天进行。为了达到这个目的，原来的跑道必须分为两个跑道，每天使用一个跑道。第一天，起点为路口 0，终点为一个“中间路口”；第二天，起点是那个中间路口，而终点为路口 N。对于给出的良好的跑道，你的程序要确定“中间路口”的集合。如果良好的跑道 C 可以被路口 S 分成两部分，这两部分都是良好的，并且 S 不同于起点也不同于终点，同时被分割的两个部分满足下列条件：（1）它们之间没有共同的街道（2）S 为它们唯一的公共点，并且 S 作为其中一个的终点和另外一个的起点。那么我们称 S 为“中间路口 ”。在例子中只有路口 3 是中间路口。
输入输出格式
输入格式：

输入文件包括一个良好的跑道，最多有 50 个路口，100 条单行道。
一共有 N+2 行，前面 N+1 行中第 i 行表示以编号为(i-1)的路口作为起点的街道，每个数字表示一个终点。行末用 -2 作为结束。最后一行只有一个数字 -1。

输出格式：

第一行包括：跑道中“不可避免的”路口的数量，接着是这些路口的序号，序号按照升序排列。
第二行包括：跑道中“中间路口”的数量，接着是这些路口的序号，序号按照升序排列。

分析

这个题反正理解很重要，题意大概是：

给一个有向图，共两问：
1)求所有从0到n的必经之点
2)求所有消失后就会将整个图分成不联系的两块的点（中间点）

很显然，如果一个点消失后就会将图分成不联系的两半，那么这个点就一定是必经之点，于是第二问的答案就是第一问的子集了。我们就可以每找出一个1),就判断它是否满足2)。

• 对于1):
  反正就只有50来个点，那么我们就可以一一枚举这些点，假定它们消失，从0开始深搜，看是否能够走到n。并且一边走一边标记（此题不需要回溯）

• 对于2)
  从每一个满足1)的点x开始深搜，同样是一边搜一边标记，若搜完检查时发现有同时被1)和2)标记的，就说明分开的两块“藕断丝连”，x就不可取。

细节：在1)的搜索之前，一定不可以手贱地添上：vis1[i]=1; 
           而2)可添可不添。

下面是参考代码：

c++
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
//×??àóD 50 ???·?ú￡?100 ì?μ￥DDμà?￡
struct point
{
    int to;
    int nxt;
}edge[120];
int x,y,n=0,tot=0,gg;
int head[55];
int Must[55],Mid[55],cnt1=0,cnt2=0;
int vis1[55],vis2[55];

void add(int u,int v)
{
    tot++;
    edge[tot].nxt=head[u];
    edge[tot].to=v;
    head[u]=tot;
}

bool dfs(int x)
{
    for(int i=head[x];~i;i=edge[i].nxt)
    {
        int v=edge[i].to;
        if(!vis1[v] && v!=gg) 
        {
            vis1[v]=1;
            dfs(v);
        }
    }
    if(vis1[n]) return 1;
    return 0;
}

void check(int x)
{
    for(int i=head[x];~i;i=edge[i].nxt)
    {
        int v=edge[i].to;
        if(!vis2[v])
        {
            vis2[v]=1;
            check(v);
        }
    }
}


int main()
{
    memset(head,-1,sizeof(head));
    int f=0;
    while(cin>>x && x!=-1 &&!f)
    {
        if(x==-2) continue;
        add(n,x);
        while(cin>>x && x!=-2)
        {
            if(x==-1) f=1;
            add(n,x);            
        }
        n++;
    }
    for(int i=1;i<n;i++)
    {
        gg=i;
        memset(vis1,0,sizeof(vis1));
        memset(vis2,0,sizeof(vis2));
        vis1[0]=1;
        if(!dfs(0))
        {
            cnt1++;
            Must[cnt1]=i;
            vis2[i]=1;
            check(i);
            int flag=0;
            for(int j=0;j<=n;j++)
                if(vis1[j] && vis2[j])
                {
                    flag=1;
                    break;
                }
            if(!flag)
            {
                cnt2++;
                Mid[cnt2]=i;
            }
        }
    }
    cout<<cnt1<<" ";
    for(int i=1;i<=cnt1;i++)
        cout<<Must[i]<<" ";
    cout<<endl;
    cout<<cnt2<<" ";
    for(int i=1;i<=cnt2;i++)
        cout<<Mid[i]<<" ";
    return 0;    
}