PageRank算法
PageRank是网页重要程度计算方法,可推广到有向图结点的重要程度的计算。基本思想是在有向图上定义随机游走模型,在一定条件下,极限情况访问每个结点的概率收敛到平稳分布。
给定有n个结点强连通且非周期性的有向图,在其基础上定义随机游走模型。假设转移矩阵M,在时刻0,1,2,…,t,…访问各个结点概率为

则其极限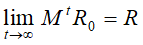 存在,那么极限向量R表示马尔可夫链的平稳分布,满足
存在,那么极限向量R表示马尔可夫链的平稳分布,满足
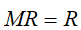
平稳分布R称为这个图的PageRank。R的各个分量为各个结点的PageRank值,

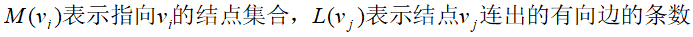
这是PageRank的基本定义,但有时有向图并未能满足强连通且非周期性的条件,没有其对应的平稳分布。
然而可以在基本定义上导入平滑项,这样平稳分布向量R就由下面的公式决定
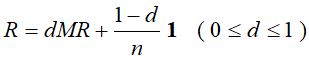
其中,1是所有分量为1 的n维向量;d阻尼因子,一般由经验决定

因此这也称为PageRank的一般定义,其随机游走模型的转移矩阵由两部分的线性组合组成,一部分是有向图的基本转移矩阵M,另一部分是完全随机的转移矩阵。
PageRank的计算方法包括幂法、迭代计算法、代数算法。
幂法是其常用的方法,通常计算矩阵的主特征值和主特征向量求求得有向图的一般PageRank。计算流程:
输入:有n个结点的有向图,其转移矩阵M,阻尼因子d,初始向量x0和计算精度ε
输出:有向图的PageRank平稳向量R
- 令t=0,选择初始向量x0
- 计算有向图的一般转移矩阵A
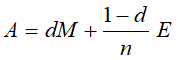
- 迭代并规范化结果向量
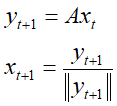
- 当时
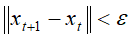 ,令
,令 ,停止迭代。
,停止迭代。
- 否则,令t=t+1,执行步骤(3)
- 对R进行规范化处理,使其表示概率分布
例,给定以下有向图,d=0.85,ε=0.005,求其一般的PageRank
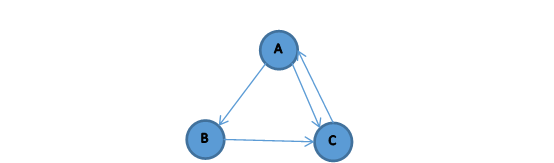
图1 有向图
有向图的转移矩阵
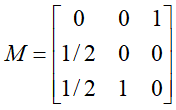
- 令t=0,
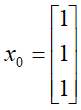
- 根据公式计算该图的一般转移矩阵A
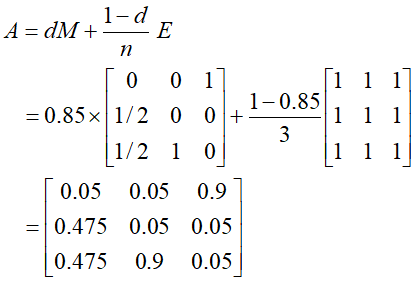
- 迭代并规范化
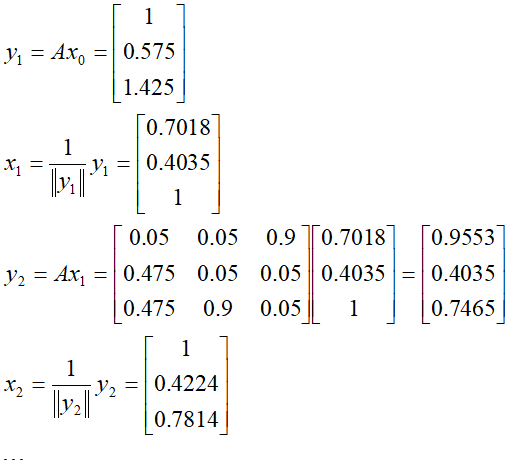
通过多次迭代,在t=21,22时,得到向量

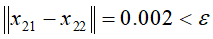 ,停止迭代,取
,停止迭代,取
将R规范化,即使得其各个分量的和为1,
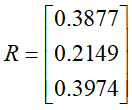
迭代计算算法的流程:
输入:有n个结点的有向图,其转移矩阵M,阻尼因子d,初始向量R0
输出:有向图的PageRank平稳向量R
(1)令t=0,
(2)计算

(3)当时
 充分接近,令
充分接近,令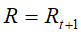 ,停止迭代。
,停止迭代。
(4)否则,令t=t+1,执行步骤(2)
代数算法的流程:
按照一般PageRank的定义
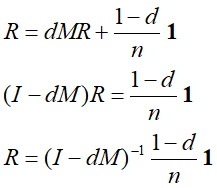
当0<d<1时,上定义式的推导解存在且唯一,这样就可通过求逆矩阵
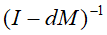 得到有向图的一般PageRank
得到有向图的一般PageRank



