XGBoost算法
XGBoost 相比于GBDT 做了两方面的优化:
一是算法本身的优化:在算法的弱学习器模型选择上,对比GBDT只支持决策树,XGBoost 还可以直接很多其他的弱学习器。
在算法的损失函数上,除了本身的损失,XGBoost 还加上了正则化部分,可以防止过拟合,泛化能力更强。
在计算方式上,GBDT的损失函数只对误差部分做负梯度(一阶泰勒)展开,而XGBoost损失函数对误差部分做二阶泰勒展开,更加准确。
二是算法运行效率的优化:对每个弱学习器,比如决策树建立的过程做并行选择,找到合适的子树分裂特征和特征值。在并行选择之前,先对所有的特征的值进行排序分组,以方便并行选择。
XGBoost 在GBDT 损失函数 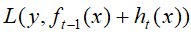 的基础上,加入正则化项
的基础上,加入正则化项 :
:
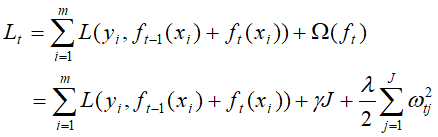
这里的 J 是叶子节点的个数,而 是叶子区域的值
是叶子区域的值
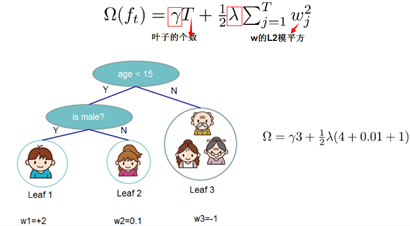
图1-1 XGBoost 正则化项
最终要极小化上面这个损失函数,得到第t个决策树最优的所有J个叶子节点区域和每个叶子节点区域的最优解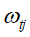 。XGBoost没有和GBDT一样去拟合泰勒展开式的一阶导数,而是期望直接基于损失函数的二阶泰勒展开式来求解。
。XGBoost没有和GBDT一样去拟合泰勒展开式的一阶导数,而是期望直接基于损失函数的二阶泰勒展开式来求解。
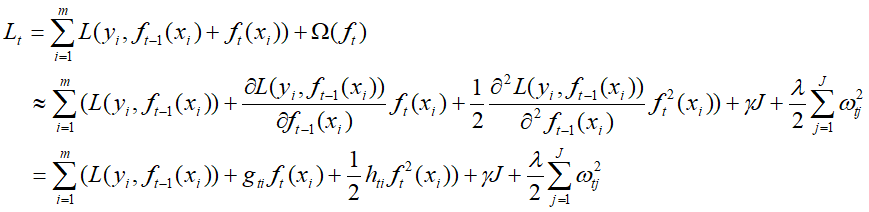
在上式的损失函数中, 是常数,对损失函数求最小化无影响,可以暂时忽略。同时每个决策树的第j个叶子节点的取值最终会是同一个值
是常数,对损失函数求最小化无影响,可以暂时忽略。同时每个决策树的第j个叶子节点的取值最终会是同一个值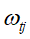 。那么上式将可以简化为:
。那么上式将可以简化为:
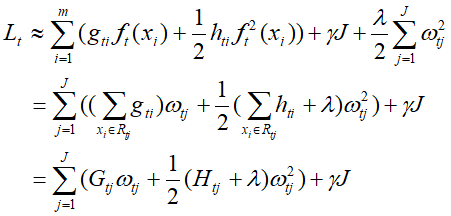
这个定义里的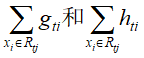 要表达的是:每个样本值xi 都能通过函数映射到树上的某个叶子节点。
要表达的是:每个样本值xi 都能通过函数映射到树上的某个叶子节点。
关于如何一次求解出决策树最优的所有J个叶子节点区域和每个叶子节点区域的最优解,可以把它拆分成2个问题:
- 如果已经求出了第t个决策树的J个最优的叶子节点区域,如何求出每个叶子节点区域的最优解?
- 对当前决策树做子树分裂决策时,应该如何选择哪个特征和特征值进行分裂,使最终我们的损失函数L最小?
对于第一个问题,可以对损失函数求导并令导数为0即可。这样就可以得到叶子节点区域的最优解
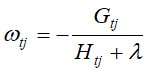
对于第二个问题,使用贪心法,即每次分裂都期望最小化损失函数的误差。
如果每次做左右子树分裂时,可以最大程度的减少损失函数的损失就最好了。假设当前节点左右子树的一阶二阶导数和分别为
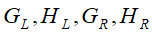 ,则最大化下式:
,则最大化下式:
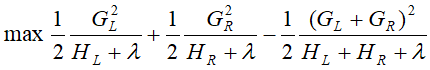
具体简单的年龄特征的例子如下,假设我们选择年龄这个特征的值a作为决策树的分裂标准,则有4种分法,分别是左子树从1人到4人的分法,然后利用上式,求能使上式得到最大值的一种分法。

图1-2 子树分裂的选择
XGBoost的算法主要流程。
输入:训练集样本
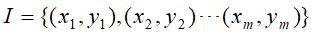 ,最大迭代次数T,损失函数L,正则化系数
,最大迭代次数T,损失函数L,正则化系数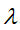
输出:强学习器
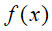
对迭代次数t=1,2,...,T有:
- 计算第i个样本在当前轮损失函数L基于
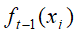 的一阶导数和二阶导数,然后累计求和得到
的一阶导数和二阶导数,然后累计求和得到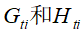
- 基于当前节点尝试分裂决策树,默认分数score=0,
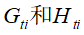 为当前需要分裂的节点的一阶二阶导数之和。
为当前需要分裂的节点的一阶二阶导数之和。
对特征序号 k=1,2...K:
a)
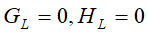
b.1) 将样本按特征k从小到大排列,依次取出第i个样本,依次计算当前样本放入左子树后,左右子树一阶和二阶导数和:

b.2) 尝试更新最大的分数:
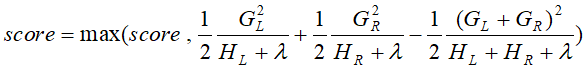
- 基于最大score对应的划分特征和特征值分裂子树。
- 如果最大score为0,则当前决策树建立完毕,计算所有叶子区域的
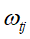 , 得到弱学习器
, 得到弱学习器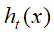 ,更新强学习器
,更新强学习器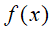 ,进入下一轮弱学习器迭代。如果最大score不是0,则转到第2)步继续尝试分裂决策树。
,进入下一轮弱学习器迭代。如果最大score不是0,则转到第2)步继续尝试分裂决策树。



