Apriori算法

Apriori原理说的是如果一个元素项不是频繁集，那么包含该元素项的超集也不是频繁集。

图1-1 Apriori搜索频繁项集的原理

Apriori 算法是发现频繁项集的一种方法。过程如下：

1. 生成所有单个物品的项集列表。
2. 接着扫描交易记录来查看哪些项集满足最小支持度要求，那些不满足最小支持度的集合会被去掉。
3. 对剩下来的项集进行组合以生成包含两个元素的项集。再重新扫描交易记录，去掉不满足最小支持度的项集。
4. 重复 步骤3 进行直到所有项集都被去掉。

   Apriori算法的实现：

   # 对项集进行过滤，保留满足最小支持度的

   def scanD(D,Ck,minSupport):

   ssCnt={}

   for tid in D:

   # 缺点：每生成一个 频繁项集，就要扫描一次数据集

   for can in Ck:

   if can.issubset(tid):

   if can not in ssCnt:

   ssCnt[can]=1

   else:

   ssCnt[can]+=1

   numItems=float(len(D))

   ret_list=[]

   supportData={}

   for key in ssCnt:

   support=ssCnt[key]/numItems

   if support >= minSupport:

   ret_list.append(key)

   supportData[key]=support

   return ret_list,supportData

    

   # 构建一个 k 个项组成的候选项集的列表

   def Ck_gen(Lk,k):

   retList=[]

   lenLk=len(Lk)

   for i in range(lenLk):

   for j in range(i+1,lenLk):

   L1=list(Lk[i])[:k-2]

   L2=list(Lk[j])[:k-2]

   L1.sort()

   L2.sort()

   if L1==L2:

   retList.append(Lk[i]|Lk[j])

   return retList

   上面两个函数做的是生成和筛选频繁项集

   def apriori(dataSet,minSupport=0.5):

   D=list(map(set,dataSet))

   # C1 是只含单个元素的项集链表

   C1=createC1(D)

   L1,supportData=scanD(D,C1,minSupport)

   L=[L1]

   k=2

   # 继续寻找后续的多元项集，从而创建包含更大项集的列表，直到下一个大的项集为空

   while(len(L[k-2])>0):

   Ck=Ck_gen(L[k-2],k)

   Lk,supK=scanD(D,Ck,minSupport)

   supportData.update(supK)

   L.append(Lk)

   k+=1

   return L,supportData

   利用前面两个函数，apriori算法从数据集中，提取出所有能满足最小支持度的项集。

   在数据集经过apriori算法的频繁项集搜索后，就能进入到下一步，关联规则的挖掘。

   # 关联规则的生成

   def gen_rules(L,supportData,minConf=0.7):

   rule_list=[]

   for i in range(1,len(L)):

   for freqSet in L[i]:

   H1=[set([item]) for item in freqSet]

   if (i>1):

   rulesFromConseq(freqSet,H1,supportData,rule_list,minConf)

   else:

   calcConf(freqSet,H1,supportData,rule_list,minConf)

   return rule_list

    

   # 计算规则的置信度

   def calcConf(freqSet,H,supportData,br1,minConf):

   prunedH=[]

   for conseq in H:

   conf=supportData[freqSet]/supportData[freqSet-conseq]

   if conf>=minConf:

   print(freqSet-conseq,'-->',conseq,' conf:',conf)

   br1.append((freqSet-conseq,conseq,conf))

   prunedH.append(conseq)

   return prunedH

    

   # 从最初的项集中生成更多的关联规则

   def rulesFromConseq(freqSet,H,supportData,br1,minConf):

   m=len(H[0])

   if( len(freqSet) >(m+1)):

   Hmp1=Ck_gen(H,m)

   Hmp1=calcConf(freqSet,Hmp1,supportData,br1,minConf)

   if(len(Hmp1)>1):

   rulesFromConseq(freqSet,Hmp1,supportData,br1,minConf)

   将这个规则挖掘算法放到测试数据集上测试：

   mushDataSet=[line.split() for line in \open('C:/Users/Lin/Desktop/ML/apriori/mushroom.dat').readlines()]

   L,supportData=apriori(mushDataSet,minSupport=0.3)

   rules=gen_rules(L,supportData,minConf=0.9)

   

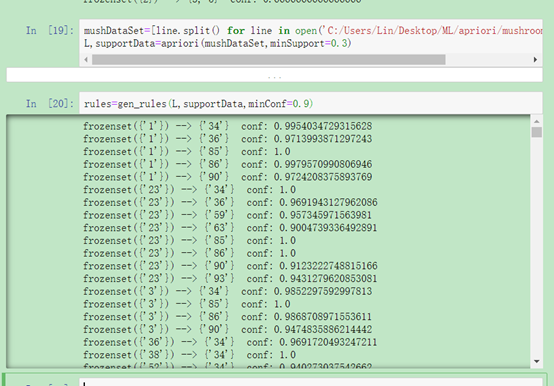
   图1-2 测试例子