《统计学习方法》笔记--蒙特卡洛法
蒙特卡洛法(Monte carlo method),也称为统计模拟方法，通过从概率模型的随机抽样进行近似数值计算的方法。
它要解决的问题是，假设概率分布的定义已知，通过抽样获得概率分布的随机样本，并通过得到的随机样本对概率分布的特征进行分析。故这种方法的核心即是随机抽样。
一般的蒙特卡洛法有直接抽样法、接受-拒绝抽样法、重要性抽样法等。
接受-拒绝抽样法（accept-reject sampling method)，适合于概率密度函数复杂，比如其概率密度函数有多个变量，各变量相互不独立，密度函数形式复杂，从而导致其不能直接进行抽样的情况。
假设p(x)不能直接抽样，接受-拒绝法先找一个可以直接抽样的分布q(x)，称为建议分布，且q(x)的c倍一定大于等于p(x)。按照q(x)进行抽样，假设得到结果是x*，按的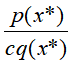
比例随机决定是否接受x*。
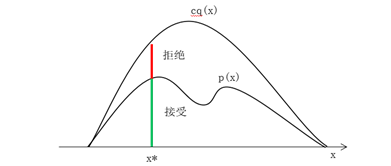
图1-1 接受-拒绝抽样法
蒙特卡洛法还可以用于数学期望估计。假设有随机变量x，其概率密度函数为p(x)，f(x)为定义在X上的函数，目标是求函数f(x)关于密度函数p(x)的数学期望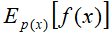
做法是按照概率分布p(x)独立地抽取n个样本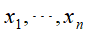
，之后计算函数f(x)的样本均值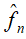
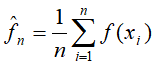
作为数学期望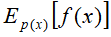
的近似值。当抽样的样本容量增大时，样本的均值以概率1收敛于数学期望。
蒙特卡洛法还可以用于定积分的近似计算，称为蒙特卡洛积分法。假设有一函数h(x)，目标是计算该函数的积分
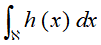
如果能够将h(x)分解成一个函数f(x)和一个概率密度函数p(x)的乘积的形式，那么就有
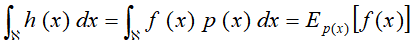
这样h(x)的积分就可以表示成一个函数f(x)关于一个概率密度函数p(x)的数学期望。而函数的数学期望又可以通过函数的样本均值估计。那么样本均值就能来近似地计算积分了。
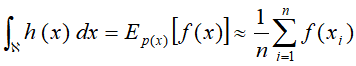
例如，用蒙特卡洛积分法求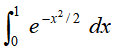
解： 令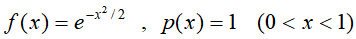
即假设随机变量x在（0，1）区间遵循均匀分布。
使用蒙特卡洛积分法，在（0，1）区间按照均匀分布抽取10个随机样本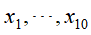
，计算样本的函数均值
样本 | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 |
f(x) | 0.043 | 0.045 | 0.054 | 0.059 | 0.076 | 0.094 | 0.111 | 0.111 | 0.115 | 0.124 |
表1-1 10个随机样本对应f(x)的值
故原式子的近似积分为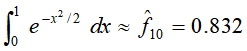
马尔可夫链的一些定义和性质
设有马尔可夫链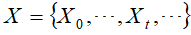
，其状态空间
，转移概率矩阵
。
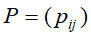平稳分布
如果存在状态空间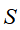
上的一个分布
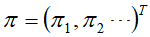使得
生成，则称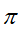
为马尔可夫链
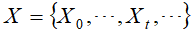的平稳分布。
也即，以该平稳分布作为初始分布，面向未来进行随机转给转移，之后的任意一个时刻的状态分布都是该平稳分布。
分布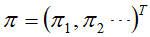
为马尔科夫链平稳分布充分必要条件为
是下列方程组的解：
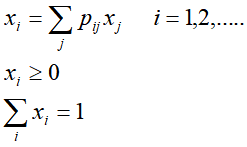
例如有图1-2 的马尔可夫链，其转移概率矩阵为
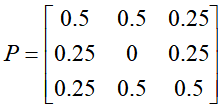
求其平稳分布。
图1-2 实例马尔可夫链
解：设平稳分布为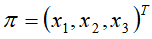
，有方程组得
解方程组，得到唯一的平稳分布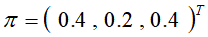
不可约性
如果时刻0从状态j起，时刻t为状态i的概率大于0，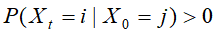
，则称此马尔可夫链是不可约的。
也即，一个不可约的马尔可夫链，从任意状态出发，经过充分长的时间后，可以到达任意状态。
而下图的马尔可夫链是可约的，
图1-3 可约的马尔可夫链
通过计算，该马尔可夫链的平稳分布为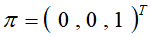
，表明此链，转移到状态3后，就在该状态上循环跳转，不能到达状态1和状态2。
非周期性
如果一马尔可夫链在时刻0从状态i出发，时刻t返回到该状态i的所有时间长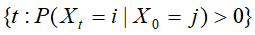 
的最大公约数是1，则称此马尔可夫链是非周期的。
也即，一个非周期性的马尔可夫链，不存在一个状态，从这个状态出发，再返回到这个状态时所经历的时间长呈一定的周期性。
而下图的马尔可夫链是周期的，
图1-4 周期的马尔可夫链
通过计算，该马尔可夫链的平稳分布为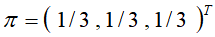
，表明此链，从每个状态出发，返回该状态的时刻都是3的倍数，具有周期性，最总停留着每个状态的概率都为1/3。
正常返性
定义概率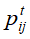
为马尔可夫链在时刻0从状j出发，时刻t首次转移到该状态i的概率，即
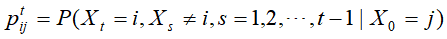，若对所有的状态i，j都满足
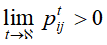，则称此马尔可夫链是正常返的。
也即，一个正常返的马尔可夫链，其中任意一个状态，从其他任意一个状态出发，当时间趋近于无穷是，首次转移到这个状态的概率不为0。
可逆马尔可夫链
如果任意状态i，j，对任意一个时刻t满足
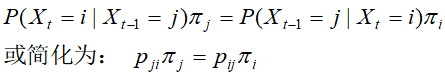
则称此马尔可夫链为可逆马尔可夫链，上面的等式组也称细致平衡方程。
也即，一可逆马尔可夫链，以平稳分布作为初始分布，进行随机状态转移，无论是面向未来还是面向过去，任何一个时刻的状态分布都是该平稳分布。
而下图的马尔可夫链是不可逆的，
图1-5 不可逆的马尔可夫链
通过计算，该马尔可夫链的平稳分布为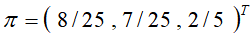
，不满足细致平衡方程。
而通过分析和推理，能得到：
- 不可约且非周期的有限状态马尔可夫链，有唯一平稳分布存在
- 不可约、非周期正常返的马尔可夫链，有唯一平稳分布存在
- 可逆的马尔可夫链一定有唯一平稳分布存在
