《统计学习方法》笔记--概率潜在语义分析
概率潜在语义分析(probabilistic latent semantic analysis，PLSA)是一种利用概率生成模型对文本集合进行话题分析的无监督学习方法。
跟潜在语义分析相似，而其特点是基于概率模型，用隐变量表示话题；整个模型表示文本生成话题，话题生成单词，从而得到单词-文本共现数据的过程。
概率潜在语义分析模型有生成模型，以及等价的共现模型。
假定n个文本的集合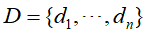
，文本中所有单词的集合
；设定K个话题，他们为集合
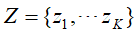，多项概率分布P(d)表示生成文本d的概率,多项条件概率分布P(z|d)表示文本d生成话题z的概率,多项条件概率分布P(w|z)表示话题z生成单词w 的概率。
生成模型
生成模式通过以下步骤生成文本-单词共现数据：
（1）依据概率分布P(d)，从文本集合中随机选取一个文本d，共生成N个文本；针对每个文本，执行下一步操作，
（2）在文本d给定条件下，依据条件概率分布P(z|d)，从话题集合中随机选取一个话题z，共生成L个话题，
（3）在话题z给定条件下，依据概率分布P(w|z)，从单词集合中随机选取一个单词w。
生成模型属于概率有向图模型，可以用以下的图表示，
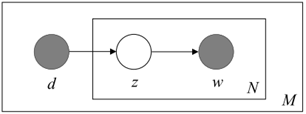
图1-1 概率潜在语义分析的生成模型
从数据生成过程可推出文本-单词共现数据T的生成概率为所有单词-文本对（w，d）的生成概率乘积，
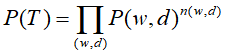
而每个单词-文本对（w，d）的生成概率由以下公式决定：
共现模型
同样，文本-单词共现数据T的生成概率为所有单词-文本对（w，d）的生成概率乘积：
但每个单词-文本对（w，d）的生成概率由以下公式决定：
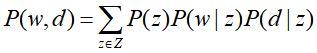
共现模型假设在话题z给定的条件下，单词w与文本d是条件独立的，即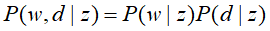
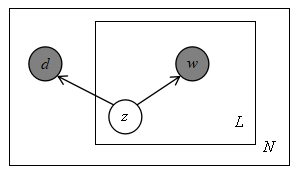
图1-2 概率潜在语义模型的共现模型
虽然生成模型与共现模型在概率公式的意义上是等价的，但拥有不同的性质。生成模型刻画文本-单词共现数据生成的过程，且单词变量w与文本变量d是不对称的，而共现模型描述文本-单词共现数据的拥有过模式，单词变量w与文本变量d是对称的。
生成模型的EM算法
概率潜在语义分析模型是含有隐变量的模型，其学习通常使用EM算法。
目标是估计概率潜在语义分析生成模型的参数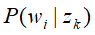
和
，使用极大似然估计，在其对数似然函数是：
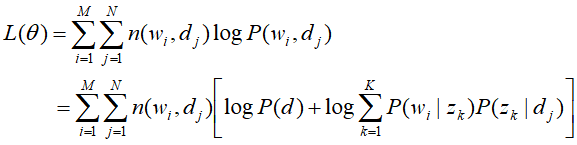
其中P(d)与需要估计的参数无关，将其舍去也不影响结果，那么代求问题也将变为舍去无关项后对数似然函数的极大问题，
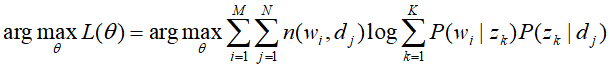
然而，z 是隐变量，无法观测到，则这个公式的最大化，需要再做一个变化，同时乘上和除以P(z|d,w)
那么上式log的右边就变成了关于z的函数的期望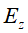
，式子成为
再根据Jensen不等式，有
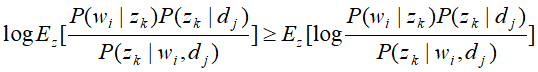
这样再已知P(z|d,w)的条件下，可以求到
的下界，其中
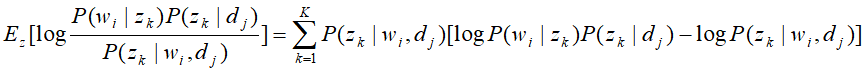
再将与要估计的参数的无关项舍去，问题就变成了
该函数也即为EM算法E步骤中的Q函数，完全数据的对数似然函数对不完全数据的条件分布的期望，设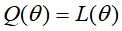
在Q函数中P(z|d,w)可以根据贝叶斯公式计算
到此，完成了EM算法的E步，接下来是M步，最大化
，求出新的参数
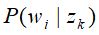和
，而这参数变量满足约束条件
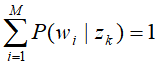和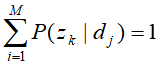
，引入拉格朗日乘子，定义拉格朗日函数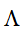
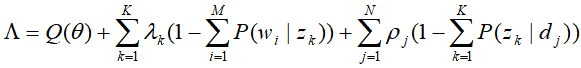
对其分别对求偏导数，并令其为0，得到方程组
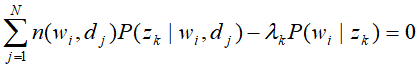
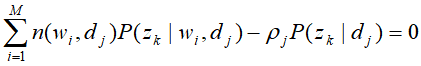
解方程组得到M步的参数估计公式：
M步求最大化，即最大化Q函数以估计我们所需的参数。然后根据新的参数求p(z|d,w)，再写出新的下界函数，再最大化…反复迭代直至收敛。这就是将EM算法应用到PLSA的求解中。
