《统计学习方法》笔记--潜在语义分析

单词向量空间

通常文本的语义内容表示可以用一个简单的模型来表示--单词向量空间模型。

即对于一个给定的文本，用一向量表示该文本的语义，向量的每一个维度表示一个单词，其数值为该单词在文本中出现的频数或权数。而模型的基本假设是文本中所有单词的出现情况即表示该文本的语义内容。

关于不同文本之间的语义相似度的度量，则可以用文本在单词向量空间中所表示的向量进行内积，而内积值的大小对应了文本之间语义相似度的情况。

单词向量空间模型的定义，假定n个文本的集合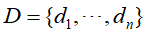，文本集合中的所有单词的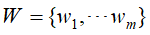。将单词在文本中出现的情况用一个单词-文本矩阵表示，记作X

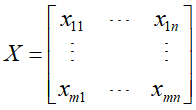
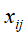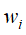元素表示单词在文本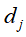中出现的频数或权值。而权值通常用单词频率-逆文本频率（term frequency-inverse document frequency，TF-IDF）表示，

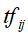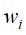式子中是单词在文本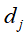中出现的频数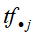，是文本中的单词总数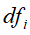，是含有单词的文本数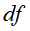，是文本总数n。这个式子能直观表示，一个单词在一个文本中出现的频数越高，这个单词在这个文本中的重要度就越高；一个单词在整个文本集中出现的出现的文本数越少，这个单词就越能表示其所在文本的特点。

现用一个单词-文本矩阵，如下，对其进行语义分析

 

	d1	d2	d3	d4
Airplane	2
aircraft		2
computer			1
Apple			2	3
fruit				1
produce	1	2	2	1

表1-1 单词-文本矩阵例

根据文本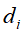和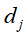在单词向量空间中所表示的向量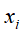和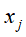，进行内积运算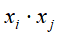，用来表示它们之间的语义相似度。表1-1中d1和d2的对应向量内积为2，得出它们的相似度并不高，尽管它们的内容比较相似。d3和d4的对应向量内积为8，得出它们的相似度比较高，但它们的实际内容却并不相似。

而从单词向量空间模型的优缺点看，就能明白上面的结果是怎么一回事了。

这个模型的优点是它比较简单，计算效率较高。但其缺点是在一词多义及多词一义的情况下，其相似度的计算就变得不准确。

比如，在上面文本d1和d2中airplane和aircraft被当作了两个独立的单词了。在d3中apple可能表示apple computer，而在d4中apple可能表示fruit，却在这模型中被当作同一个单词。

 

话题向量空间

为了解决基于单词向量空间模型存在的问题，有一种话题向量空间模型（topic vector space model），其先定义了话题向量空间，用来表示话题和单词之间的关系，设单词-话题矩阵为T（共有k个话题）

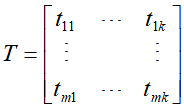
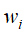元素表示单词在话题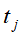中出现的权值，权值越大，该单词在此话题中的重要度就越高。

然后，文本在话题空间的表示可定义为话题-文本矩阵Y

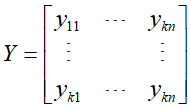
元素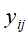表示文本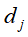的语义内容为话题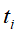的可能性。

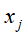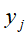这样一来，在单词向量空间的文本可以通过它在话题空间中的向量近似表示，具体地由k个话题向量以为系数的线性组合近似表示：

即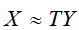，而这也正是潜在语义分析。在话题向量空间中，文本的相似度可由它们在话题空间中所表示的对应向量的内积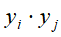进行表示。

潜在语义分析的思路是对单词-文本矩阵X进行奇异值分解，将其左矩阵作为单词-话题矩阵T，对角矩阵和右矩阵的乘积作为话题-文本矩阵Y。

假设话题的个数为k，对单词-文本矩阵X进行截断奇异值分解：

现有一单词-文本矩阵X，其元素表示单词在文本中出现的频数，如下

Index words	D1	D2	D3	D4	D5	D6	D7	D8	D9
books			1	1
dads						1			1
dummies		1						1
estate							1		1
guide	1					1
investing	1	1	1	1	1	1	1	1	1
market	1		1
real							1		1
rich						2			1
stock	1		1					1
value				1	1

表1-2 潜在语义分析的单词-文本矩阵

对矩阵X进行截断奇异值分解，得

将矩阵X进行截断奇异值分解后，单词-话题矩阵和话题-文本矩阵都存在值小于0的元素，而这些元素却无法进行正常解释。

 

非负矩阵分解算法

为消除这现象，可将矩阵X进行非负矩阵分解。

非负矩阵为矩阵中的所有元素值都大于等于0，若X为非负矩阵，则记为。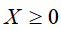

给定非负矩阵X，找到两个非负矩阵W和H，使得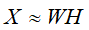，即称其为矩阵X的非负矩阵分解。

非负矩阵分解可形式化为最优化问题来求解。首先定义损失函数。

第一种是平方损失，两非负矩阵A和B的平法损失函数为：

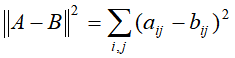
另一种散度，两非负矩阵A和B的散度损失函数为：

然后单词-文本矩阵X的非负矩阵分解就可以根据损失函数和条件进行转化为求解最优化问题：

平方损失函数的目标函数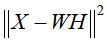，关于W和H的最小化，满足约束条件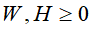，即

散度损失函数的目标函数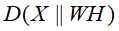，关于W和H的最小化，满足约束条件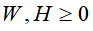，即

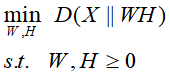
这两种方法都可以用梯度下降法求解，得到的W和H矩阵分别为单词-话题矩阵和话题-文本矩阵。