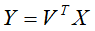《统计学习方法》笔记--主成分分析

主成分分析(principle component analysis,PCA)，用正交变换将由线性相关变量表示的观测数据转换为少数几个由线性无关变量（称主成分）表示的数据的方法，即对数据进行降维处理。

这种方法的几何解释即是将样本映射到几个相互正交的向量上，并使得样本在所映射的向量上方差最大，

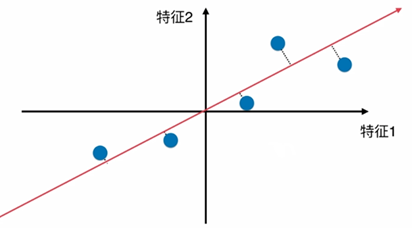
图1-1 样本在单个向量上的映射

可以定义N个样本在所映射的单个向量上方差Var

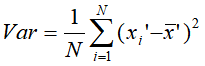
其中x'为样本在所映射向量上的坐标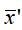，为N个样本在所映射向量上的坐标均值。

而主成分分析方法主要有两种，可以通过样本矩阵的奇异值分解或对相关矩阵的特征值分解进行。

相关矩阵的特征值分解算法步骤：

(设样本X为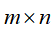矩阵，m为特征维度数，n为样本的个数)

(1)因为样本的各个维度的度量尺度可能不同，需要对样本进行规范化处理，处理如下：

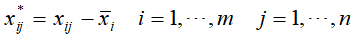
其中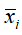，为n个样本在第i个特征维度上的均值

(2)对规范化后的数据矩阵，计算样本相关矩阵R(样本的相关矩阵为样本各分量之间的线性相关关系的一种度量)

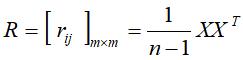
(3)求解相关矩阵R的前k个值最大的特征值和对应的单位特征向量，求得特征值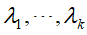，对应特征向量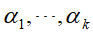，并将这些特征向量构造成正交矩阵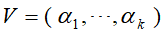

这样，V矩阵的每一列对应一个主成分，得到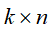样本主成分分析矩阵

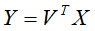
奇异值分解算法步骤：

(设样本X为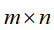矩阵，m为特征维度数，n为样本的个数)

(1)同样对样本进行规范化处理，并返回到X上

(2)对规范化后的数据矩阵X，设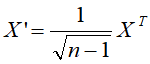

对矩阵X'进行截断奇异值分解，保留k个奇异值和其对应的奇异向量，得到

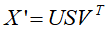
这样，V矩阵的每一列对应一个主成分，得到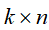样本主成分分析矩阵