《统计学习方法》笔记--奇异值分解
奇异值分解（singular value decomposition，SVD）一种矩阵因子分解的方法，在主要成分分析和潜在语义分析都会用到这一重要的工具。
其即是将一个
的实矩阵A，表示成三个实矩阵乘积形式，
其中U是m阶的正交矩阵，V是n阶的正交矩阵，而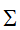
是由A矩阵的奇异值
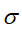由降序排列成对角线组成的
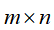对角矩阵。
分解的几何解释是将任意一个n维向量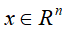
，根据公式从右到左，先经过坐标系的旋转或反转变换
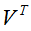，再经过坐标轴的放缩变化
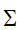，以及坐标系的旋转或反转变换
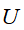，最后得到向量
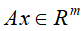，变换图像如下
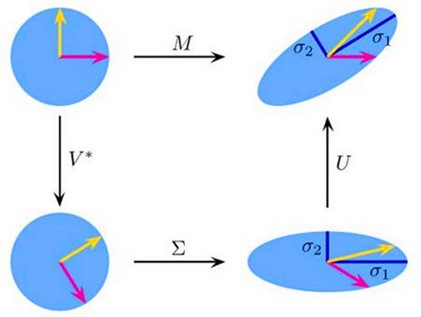
图1-1 奇异值分解的几何解释图
在实际应用中，奇异值分解可用于对矩阵进行压缩，分为紧凑形式和截断形式的。紧凑形式是将矩阵分解后，奇异值矩阵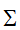
的秩与原矩阵的秩相等，对应着数据的无损压缩；而截断形式的则是将矩阵分解后，奇异值矩阵
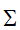的秩小于原矩阵的秩，对应着数据的有损压缩。
奇异值分解的计算可以根据奇异值分解的性质进行计算，所利用到的性质主要有：
-
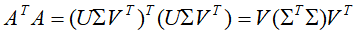
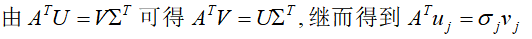
因此奇异值分解算法可如下：
输入：矩阵A；
输出：左奇异矩阵
，奇异值矩阵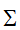
和右奇异矩阵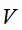
(1)先求
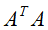的特征值和特征向量，
由
得到特征值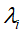
（其中前r个大于零，剩余的值为0），并将其从大到小排序；将排好序的特征值代入方程求得对应特征向量
；
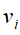(2)将特征向量单位化，得到的单位化的特征向量构成右奇异矩阵
；
(3)将求得的
排好序的特征值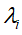
开平方，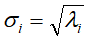
，并其将构造成
的对角矩阵
，即奇异值矩阵
；
(4)根据
求得A的前 r 个正奇异值的对应的左奇异矩阵的前 r 个列向量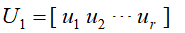
再由
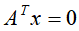求奇异值为0对应的左奇异矩阵的列向量
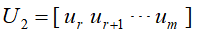，则左奇异矩阵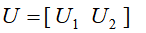
用 sklearn 简单实现 SVD 对图像的压缩测试
import numpy as np
import numpy.linalg as la
import matplotlib.pyplot as plt
from skimage import io
#获取图片并转化为矩阵
def getImgFromFileToMat(filename):
img = io.imread(filename, as_grey=True)
return np.mat(img)
def compressWithSVD(img, k):
# 获得图像的左奇异矩阵U，奇异值矩阵s和右奇异矩阵V
U, s, V = la.svd(img)
# 选择三个矩阵的前k个元素
Uk = U[:, 0:k]
Sk = np.diag(s[0:k])
Vk = V[0:k, :]
#利用三个截断矩阵恢复图像
img_new = Uk * Sk * Vk
return img_new
#显示图片
def showImg(imgMat):
plt.imshow(imgMat, cmap=plt.cm.gray)
plt.show()
可以看到k越小时，图像被压缩的越厉害，损失越大。
而损失的大小可根据弗罗贝尼乌斯范数和其引理
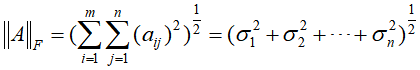
进行计算，假设原矩阵A的秩为r，进行截断式奇异值分解后，得到秩为k(k<r)的奇异值矩阵
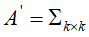，则分解后，其损失函数为 L
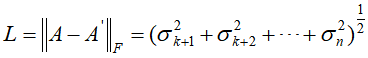
即损失了原矩阵的奇异值矩阵后面n-k个非零奇异值的范数。
