《统计学习方法》笔记--EM算法
EM（expectation maximization algorithm）用于含有隐变量的概率模型参数的极大似然估计。
例子：
有三枚A，B，C硬币。首先A为选择硬币，对其进行投掷，其投掷结果正则选择B硬币进行投掷，反为选择C硬币，然后根据选择的硬币再进行投掷，记录该硬币的投掷结果，正面为1，反面为0；重复上述过程。投掷实验过程如下，
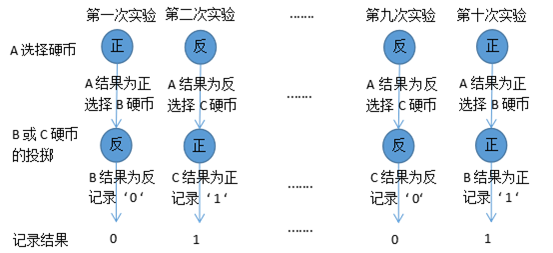
图1-1 投掷A,B,C硬币实验
实验的记录结果为：0,1,1,0,1,1,1,0,0,1
现假设只能看到掷硬币的结果（如下），不能看到过程，即表示看不到所记录的结果'1'和'0'是由B硬币还是由C硬币掷出来的，也等同于看不到 A选择硬币的投掷结果，试估计这三枚硬币出现正面的概率分别是多少。
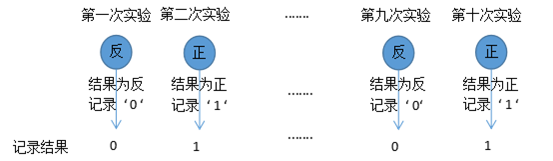
图1-2 只能看到掷硬币的结果
因此，这三硬币的一次试验的模型可以写作如下：
那么，根据总的十次试验观测数据得到模型的似然函数如下，
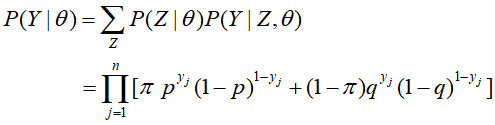
再对似然函数求极大化，便可这三枚硬币出现正面的概率分别是多少，
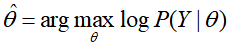
然而，对于上述的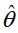
是没有解析解的，只能通过迭代求，而EM算法就是用于求解该问题的一种迭代算法。
首先，选取参数的初始值，例如上述的三枚硬币的投掷问题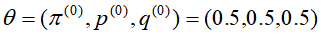
，接着进行迭代（i，表示第i次迭代），重复EM步骤，直到参数的估计值趋于稳定；
E步：在模型参数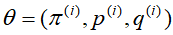
下计算，
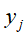来自Ｂ硬币的概率
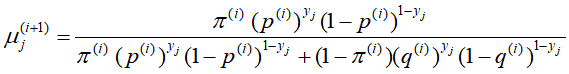
M步：更新参数，
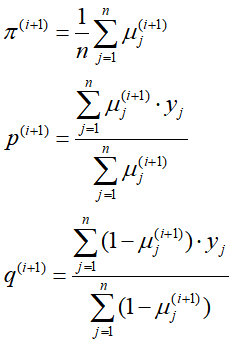
根据上面的EM步骤，三枚硬币在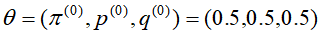
的初始参数下，每次迭代的结果如下
第一次迭代的E步骤：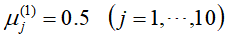
第一次迭代的M步骤：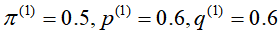
第二次迭代的E步骤：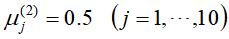
第二次迭代的M步骤：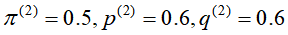
参数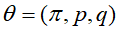
趋于稳定，故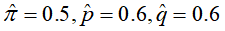
如果初始值取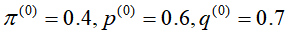
，那么得到参数的极大似然估计则为
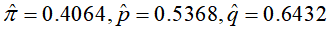，可见EM算法初始值的不同将得到不同的估计结果。
EM算法流程：
输入：观测变量数据Y，隐变量数据Z，联合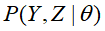分布
。条件分布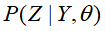
；
输出：模型参数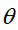
；
- 选择参数的初始值
进行迭代
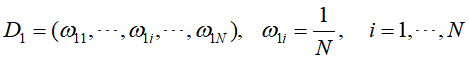
- E步：
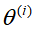为第i次迭代的参数估计值，在第i+1次迭代的E步中，计算
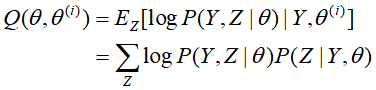
（3）M步：求使
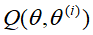极大化的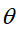
，确定下一次（第i+1次）迭代的参数估计值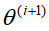
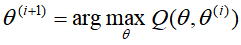
（4）重复（2），（3），直至收敛。
在EM算法的流程中Q函数为完全数据的对数似然函数
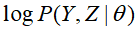，关于在给定观测数据Y和当前参数
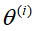下，其对未观测数据Z的条件概率分布的
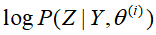期望。
