隐马尔可夫模型
隐马尔可夫模型(Hidden Markov Model,HHM),作为一种统计模型,描述了含有隐含未知数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数。
用一个掷骰子的例子来引入隐马尔可夫模型。
假设现有三种不同的骰子,第一种是四面体(称这个骰子为D4),可掷出1,2,3,4这4个数值,每个数值被掷出的概率为1/4;第二种是六面体(称D6),可掷出1,2,3,4,5,6这6个数值,每个数值被掷出的概率为1/6;同样,第三种是八面体(称D8),可以以1/8的概率掷出1到8中的其中的一个数。
如果每次可用任意一种骰子投掷,那么在投掷10次后,我们可能会得到这样一串顺序数字:3 5 4 6 2 8 4 6 1 3,而所得到的这串数字称为可见状态链。现在我们要根据这一串顺序数字,求相应的骰子序列能投掷出这一串数字。能掷出这样一串顺序数字的骰子序列可能为:D6 D8 D8 D6 D4 D8 D6 D6 D4 D8,而称这对应的骰子序列成为隐含状态链。

图1-1 掷骰子对应的隐马尔可夫模型
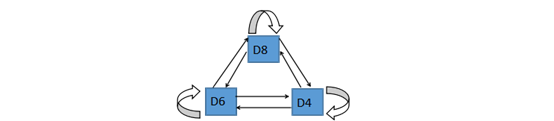
图1-2 隐含状态链中状态间的转换
在隐马尔可夫模型中,隐含状态链的状态之间存在一个转换概率。比如上面的例子,下一次掷骰子选到任意一种骰子的概率都为1/3,不过通常转换概率不是均匀的。而在可见状态链中状态间没有转换概率,不过有一个从隐含状态链中的隐含状态转化到可见状态链中可见状态的输出概率。比如上面6面体骰子掷出6的概率为1/6,而掷出8的概率为0。
至此,隐马尔可夫模型,有N个隐含状态集合 ,对应有M个可见状态集合
,对应有M个可见状态集合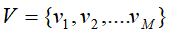 ,且其还有三个要素组成模型
,且其还有三个要素组成模型 :(集合和状态序列链是有区别的,状态序列链是从集合中选取状态组成了一个序列链条)
:(集合和状态序列链是有区别的,状态序列链是从集合中选取状态组成了一个序列链条)
- 状态转移概率矩阵A,
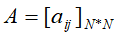 ,
,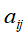 即t时刻状态
即t时刻状态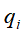 条件下,t+1时刻为状态
条件下,t+1时刻为状态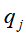 的概率
的概率 - 隐含状态的输出概率矩阵B,
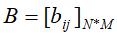 ,
, 即t时刻下状态
即t时刻下状态 输出为状态
输出为状态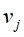 的概率
的概率 -
初始状态的概率向量
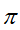 ,
,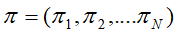 ,为初始时刻,状态为
,为初始时刻,状态为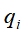 的概率
的概率 同样,根据隐马尔可夫模型的这些要素,再结合可见状态序列链
 与隐含状态序列链
与隐含状态序列链 的是否已知情况,可产生三个基本的问题:
的是否已知情况,可产生三个基本的问题:1.已知已知模型
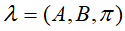 ,计算能产生某一种给定的可见状态链
,计算能产生某一种给定的可见状态链 的概率
的概率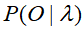
2.已知模型
 和某一种可见状态链
和某一种可见状态链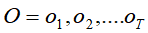 ,求能最大可能产生出这次可见状态序列对应隐含状态序列
,求能最大可能产生出这次可见状态序列对应隐含状态序列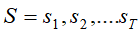 ,即使的概率最大
,即使的概率最大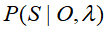
3.给出大量的可见状态链
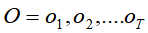 ,推算出模型的三个要素A,B,
,推算出模型的三个要素A,B, 参数,使
参数,使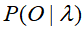
这三种问题分别有其对应的解决方法:
第一种问题的解决方法 -- 向前-向后算法。
向前算法,首先先初始化向前概率,初始N个隐含状态
 和产生对应的可见状态
和产生对应的可见状态 的联合概率
的联合概率 ,再利用向前公式
,再利用向前公式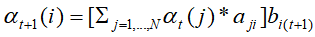 递推到最后一刻各个隐含状态
递推到最后一刻各个隐含状态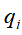 能产生对应可见状态
能产生对应可见状态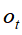 的概率
的概率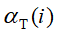 ,最后再总和
,最后再总和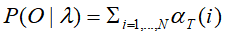 便能得到。
便能得到。 同理,向后算法,则是从后往前推出能产生对应可见状态链
 的概率。
的概率。 向前和向后算法是一种累计概率的算法,即求有多少种可能的隐含状态序列能产生对应可见状态序列链
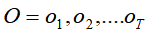 占N种隐含状态T次排列组合所产生隐含状态链数量的比。
占N种隐含状态T次排列组合所产生隐含状态链数量的比。 第二种问题的解决方法--维比特算法。
维比特算法是一种求最优路径的算法,即求某一隐含状态链
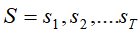 能最大可能的产生出对应已知的可见状态链
能最大可能的产生出对应已知的可见状态链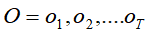 。
。 维比特算法和上述的向前算法有相似之处,都是当前的状态往后推,不同的是,向前算法求的是累计概率,而维比特算法求的是最大概率。

图1-3 向前算法和维比特算法
在时间复杂度上,维比特算法的时间复杂度为O(T*N^2)。
第三种问题的解决方法有两种,分别是监督学习和baum-welch算法。
监督学习,给定大量个长度相同的可见序列链和隐含状态序列链
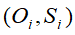 作为训练集,使用极大似然估计法来估计模型的参数
作为训练集,使用极大似然估计法来估计模型的参数 种的三个要素。
种的三个要素。 转移概率
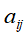 的估计,样本中t时刻处于状态
的估计,样本中t时刻处于状态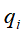 ,t+1时刻转移到状态
,t+1时刻转移到状态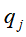 的频数为
的频数为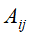 ,则
,则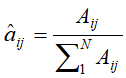 。同样,利用相同的方式计算发射概率
。同样,利用相同的方式计算发射概率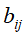 和初始状态概率
和初始状态概率 。
。baum-welch算法则是利用EM算法得到模型参数的估计式,然后通过迭代进一步优化模型的参数。
向前向后算法链接:https://zhuanlan.zhihu.com/p/41912745







