图论
一.图的拓扑排序
拓扑排序是对有向无圈图的顶点的一种排序,而拓扑排序的序列的顺序是不一定的,因为在选取入度为0的顶点的时候,可选的顶点的个数可能不止一个,选择的顶点不同,最终的拓扑排序的序列顺序也可能因此不同。
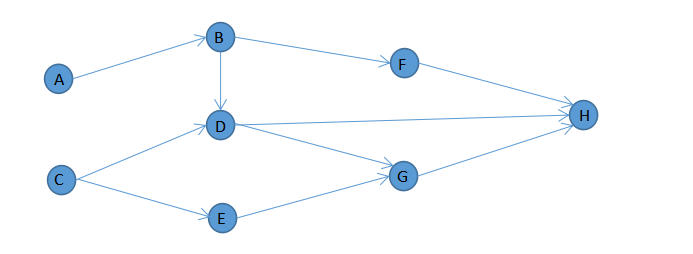
图1-1 对有向无圈拓扑排序
对图1-1中的有向无圈图进行拓扑排序,可得到排序序列有:A->B->C->D->E->F->G->H,但这排序序列不是唯一的。
根据拓扑排序的算法,能对其进行简单的代码实现,如下
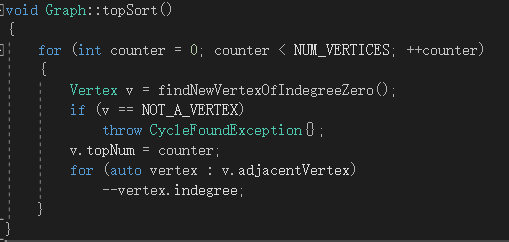
图1-2 拓扑排序代码的简单实现
该算法并不是一个最优的算法,在函数findNewVertexOfIndegreeZero( )中,其都对每个顶点进行了扫描,导致该算法的运行时间为O(|V|^2)。
可以对该算法进行一些改进,即利用队列,在将邻接顶点的入度进行修改的时候,如果邻接顶点的入度为0,则将该邻接顶点插入到队列中。在访问修改完一顶点的所有邻接顶点后,选取队列中的下一顶点进行操作。这样,拓扑排序的代码可优化如下
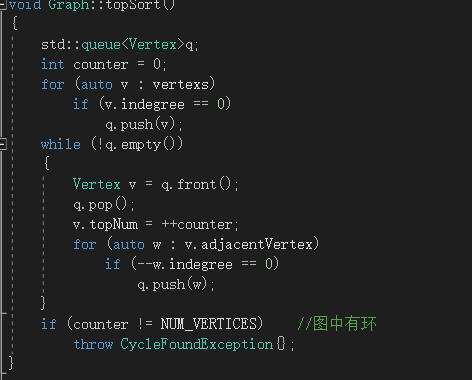
图1-3 利用队列优化的拓扑排序代码
在使用邻接表的图中,此优化的拓扑排序的运行时间为O(|E|+|V|)。
拓扑排序可以应用到图的关键路径的分析中,如下图,各顶点代表事件,而顶点之间的边权值则表示从一事件到另一事件所需要消耗的时间。分析关键路径可以得出整个方案的完成时间,并且在对关键路径上的耗时进行缩短或延长时,将可能影响整个方案的完成时间。
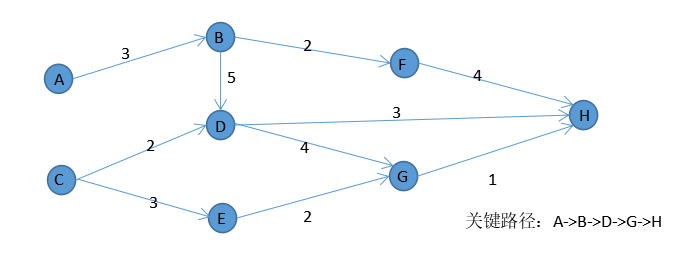
图1-4 时间节点图的关键路径
拓扑排序可以应用到图的关键路径的分析中,通过拓扑排序算出各顶点的最早完成时间ECi,运算法则为
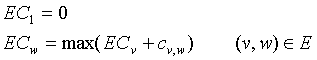
而各顶点的最晚完成时间LCi 通过逆拓扑排序计算,对应法则如下
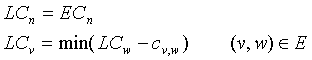
在得出各顶点所代表的事件的最早完成时间和最晚完成时间后,即可以根据各顶点的最早完成时间和最晚完成时间是否相等来确定关键路径上的顶点,在顶点确定后,确定连接这些顶点的边构成的路径即关键路径。
也可以通过计算每条边的松弛时间(相邻的目标事件最晚完成时间-本事件最早完成时间-两事件之间的耗时)确定关键路径,松弛时间的计算如下:
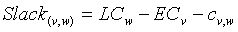
当
边的松弛时间为0时,改变为关键路径上的一边,而从起点连接到终点的松弛时间为0的边即构成一条关键路径。
不过关键路径可能不止只有一条,有时一个图可能有多条关键路径。
二.图的最短路径算法
图的最短路径算法指从一个顶点到其余顶点的最短路径,对于路径是否有权值分为无权最短路径和有权最短路径。
1.无权最短路径
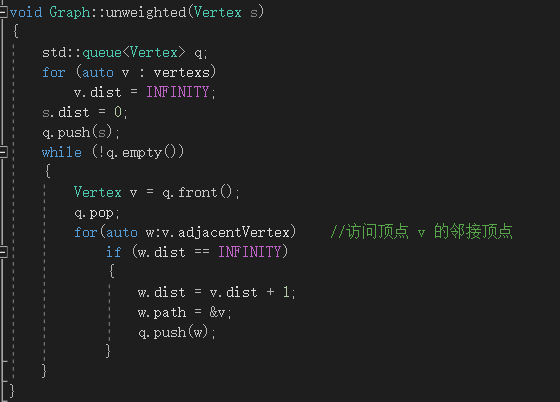
在无权路径中,最短可以理解为从某一目标到特定目标需要经过多少步骤。对于无权路径的算法实现,可以跟拓扑排序一样利用队列将求无权路径的算法进行优化,使其的运行时间为O(|E|+|V|)。
最短无权路径的算法实现如下图2-1,
2.有权最短路径算法--Dijkstra算法
Dijkstra算法能够得到单源顶点到其余顶点的最短带权路径,其实现代码如下,

Dijkstra算法中,函数findUnknowVertexWithSmallestDist()对所有顶点进行了扫描,从而使算法的时间复杂度在O(|E|+|V|^2)=O(|V|^2)。
如果使用Dijkstra算法的图是稠密图,图的边数E约等于顶点数的平法,则该算法与图的边数呈线性关系。如果是稀疏图,则算法的时间复杂度与顶点数的平方呈线性关系。
然而对于函数findUnknowVertexWithSmallestDist()可以使用堆进行代替,从而使寻找最小路径的边的操作转化为堆的寻找最小者的操作,进而将Dijkstra算法的时间优化为O(|E|log|V|)。
在前面Dijkstra算法的分析与应用中,图边的权值都是正值,对于带有负值的图,最短路径的分析却不能通过简单的将负值加上一定值转化为正值来进行求解。
三.最小生成树
图最小生成树有两种算法,分别是Prim算法和Kruskal算法。
1.Prim算法
Prim算法和Dijkstra算法基本相同,实现上也大致相同,不过Prim算法是在无向图上进行的。
2.Kruskal算法
Kruskal算法与Prim算法不相同,Kruskal算法是从图的边着手,每次从挑选权值最小的边放入到森林中,然后进行检测,若没有使图构成回路则保留改变,反之则放弃改变,继续选择下一条边进行,直到n-1条边被并入到各自独立的顶点森林中形成树。基于邻接矩阵的算法实现如下,

图3-1 Kruskal算法实现
四.深度优先搜索的应用
深度优先搜索的应用首先是寻找图的割点。
割点即为一个无向连通图删除该点后不再连通的点。它的作用类似于中间枢纽,若去除或破坏这中间枢纽,则使得枢纽两边的节点不再有联系。
如下面具有割点C和D的图,若去除C点,则G点成孤立的点,不再于其他点有联系。若去除D点,则E和F点于其他点不再有联系。

图4-1 具有割点C和D的图
一个无向图割点的确定可以通过深度优先搜索的应用找出。先利用深度优先搜索按访问顺序对顶点进行编号Num(v),然后对深度优先搜索生成的树进行后续遍历,计算编号的最低顶点Low(v),即该点v可以通过零条边或多条边,甚至是背向边到达一个最低顶点,图4-1对应的深度优先树及编号。
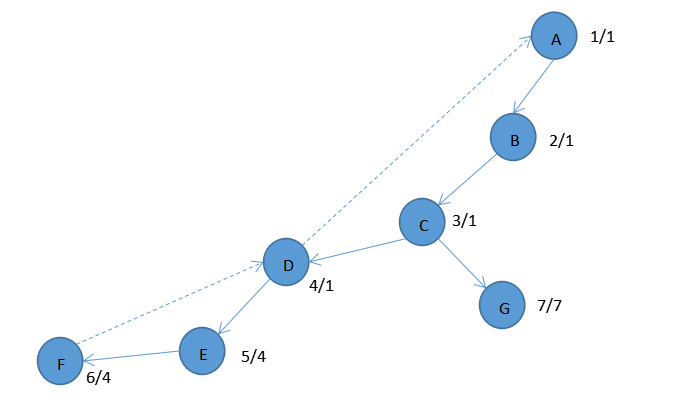
图4-2 图4-1标有(Num/Low)对应的深度优先树
根据Low的定义可知Low(v)是下列各项的最小者:
1. Num(v)。
2. 所有背向边(v,w)中的最低Num(w)。
3. 树所有边(v,w)中的最低Low(w)。
第一个条件是不选取边,第二种方法是不选取树的边而是选取一条背向边,第三种方法是选择树的某些边以及可能的背向边。
当标记好Num和Low编号后就可以判断割点,割点的判断分两类,一类是根节点的判断,另一类是其他节点的判断。根是割点当且仅当它有多于一个儿子的时候。其余顶点是割点则当且仅当它(v)有某个儿子(w)使得Low(w)大于等于Num(v)。
其次深度优先搜索还可以应用到欧拉回路的寻找和有向图强连通分支的确定等等。



