排序

内部排序的基本算法有：插入排序、希尔排序、冒泡排序、快速排序、选择排序、堆排序、归并排序、基数排序等等。

不同的算法之间有不同的时间复杂度和空间复杂度。

此外，算法之间的稳定性也是不同的。

对算法的时间复杂度、空间复杂度以及其稳定性归结如下表，

算法	时间复杂度			空间复杂度	稳定性
	最好情况	平均情况	最坏情况
插入排序	O(n)	O(n^2)	O(n^2)	O(1)	是
冒泡排序	O(n)	O(n^2)	O(n^2)	O(1)	是
选择排序	O(n^2)	O(n^2)	O(n^2)	O(1)	否
希尔排序	-	-	-	O(1)	否
快速排序	O(nlogn)	O(nlogn)	O(n^2)	O(nlogn)	否
堆排序	O(nlogn)	O(nlogn)	O(nlogn)	O(1)	否
归并排序	O(nlogn)	O(nlogn)	O(nlogn)	O(n)	是
基数排序	O(d(n+r))	O(d(n+r))	O(d(n+r))	O(d(n+r))	是

表1-1 算法性能归结表

虽然不同算法之间的性能不尽相同，但算法的选择需要考虑需要进行排序元素规模的大小、算法排序的稳定性、排序相应的应用场景和算法的可扩展性要求等等。

从考虑需要进行排序元素规模的大小的情况下，对内部排序算法方案的选择和比较如下：

1.待排序元素规模为n<10000的情形下，选择插入排序、冒泡排序和选择排序这三种基本的内部排序方法。

它们的算法实现简单，且其平均时间复杂度均为O(n^2)。

对于更小规模的排序元素（n<=25)，插入排序的效率则非常高。不过它的时间复杂度与待排序元素序列的初试排列有关。在最好情况下，只需n-1次比较便可完成，且不需要交换操作。而在平均情况和最差情况下，它的比较和交换操作都是O(n^2)。

冒泡排序与插入排序相似，在最好情况下都只需n-1次比较便可完成，且不需要交换操作。而在平均情况下和最差情况下，它们的比较和交换操作都是O(n^2)。

选择排序的关键字比较次数与待排序元素序列的初试排列无关，其比较次数总是O(n^2)，但元素的移动次数则与待排序元素序列的初试排列有关，最好情况下是不需要移动元素，而在最坏情况下其元素的移动次数也不超过3（n-1）次。

在空间复杂度上，这三种基本的内部排序算法都只需要一个辅助元素空间。对在算法的稳定性上，插入排序和冒泡排序算法都是稳定的，而选择排序则是不稳定的。

2.待排序元素规模为中等（n<=100000)的情况下，希尔排序是一种很好的选择。

在希尔排序中，算法的时间复杂度不是确定的，因为对于应用不同的增量序列，希尔排序的时间复杂度会有所不同。

对于运用希尔增量序列的

希尔排序，其在最坏情况下可证明其时间复杂度为O（n^3/2），而其平均情况下的时间复杂度则为O（n^5/4），

但这平均情况下的时间复杂度却无法得到证明。

 

虽然希尔排序的时间复杂度因增量选择的不同而不同，但其在待排序元素规模为中等的情况下，其总的元素比较次数和元素移动次数都比插入排序要少很多，且对于待排序元素个数n越大时，其效果越明显。

 

不过还需注意的是，希尔排序虽实现的代码简单，且不需要额外的辅助空间，但其是一种不稳定的排序算法。

 

3.排序元素规模n很大的情形下，可以采用快速排序、堆排序、归并排序或基数排序。

 

1.快速排序是最通用的高效的内排序算法，平均情况下它的时间复杂度为O(nlogn)，一般情况下所需要的额外空间也是O(logn)。

 

但是快速排序在有些情况下也可能退化（例如元素序列已经有序时），时间复杂度会增加到O(n^2),空间复杂度也会增加到O(n)。

 

不过我们可以通过“三数中值分割法”来避免最坏情况的发生。在这方法下，可以确立一个枢纽元将待排序元素组分成两个几乎相等子序列。

 

在快速排序中，如果子序列的元素个数小于25，可以利用插入排序来提高其总体的性能。

 

2.对于堆排序，其也是一种高效的内排序算法，它的时间复杂度是O(nlogn)，而且没有什么最坏情况会导致堆排序的运行明显变慢，而且堆排序基本不需要额外的空间。但堆排序不太可能提供比快速排序更好的平均性能。

 

3、归并排序是一个重要的高效排序算法，它的一种重要特性是性能与输入元素序列无关，时间复杂度总是O(nlogn)，归并排序的主要缺点是需要O(n)的额外存储空间。

 

4.基数排序是一种相对特殊的排序算法，这类算法不仅是对元素序列关键字进行比较，更重要的是它们对关键字的不同部分进行处理和比较。虽然基数排序具有线性增长的时间复杂度，但是由于在常规编程环境中基数排序的线性时间开销实际上不比快速排序的时间开销小，并且由于基数排序基于的关键字抽取算法受到操作系统和排序元素的影响，其适应性远不如普通的进行比较和交换操作的排序方法。

 

因此在实际工作中，常规的高效排序算法如快速排序的应用要比基数排序广泛得多。基数排序需要的额外存储空间包括和待排序元素规模相同的存储空间以及与基数数目相等的一系列桶（一般用队列实现）。

 

二.外部排序

 

对于待排序元素的规模达到一定程度或是装不进内存时，则需要用到外部排序。在外部排序中，尽管将数据读入内存的时间为O(n),但其花费的实际时间却比将已读入内存的数据进行排序的时间大很多。因为cpu的运算速度要比将磁盘中的数据读入到内存的速度快成成千上万倍。

 

外部排序首先是要构造顺串，二顺串的构造则用到了替换选择的方法。将M个记录读入到内存中并放到一个优先队列中，通过删除最小者操作，将记录输出到外部存储中，再读入下一个记录。如果读入的记录比输出的记录小，则标记此记录，当被标记记录的数量达到优先队列的大小时，构建新的顺串。

 

在所有记录都被构建成顺串时，利用归并排序里的合并算法合并顺串，从而达到将所有记录进行排序的目标。

 

对于合并顺串的方法也有多种，最基本的是进行二路合并，需要用到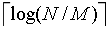趟合并。

同样，可以将二路合并扩展到多路（k）合并，对于多路（k）合并，将合并的趟数缩减到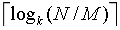，提高合并效率。

在合并中，不同的顺串的记录数量可能不同，利用Huffman树的思想构造最佳归并树，以减少外存的I/O次数，提高效率。