散列

对比前面所学的树，虽然其删除和插入操作可以达到O(logN)，而散列表却可以以常数平均时间实现同样的操作。

不过，树的O(logN)这个平均操作时间也未必比散列表的常数平均操作时间差，毕竟，树不需要去进行复杂的散列函数运算。

另外，树还可以支持那些需要序的信息从而使功能更强大的例程，比如支持范围查找或是最大最小值的查找等。而这些功能在散列表都得不到支持。

因此，散列表适合于那些不需要序的信息以及不需要对输入是否需进行排序还存疑的信息。

虽然散列表对比树各有优缺点，但散列表的应用还是比较广泛的，比如编译器中使用散列表跟踪源代码中声明的变量，在路由器上利用散列表记录IP报文头信息实现追踪等等。

散列表作为书中的章节，虽花了较多的时间学习和理解并参照了书中的部分代码做了自己的实现和测试，但对散列表的学习还需加深。

一.分离链接法

对于分离链接散列法，其优点是填因子较大时并不明显降低散列的性能，但其缺点是利用了链表（在一些编程语言中，给链表的新单元分配空间和地址比较耗时）。

template<typename hashObject>
class hashTable
{
public:
    explicit hashTable(int size = 101);

    bool contains(const hashObject & x)const;

    void makeEmpty();
    bool insert(const hashObject & x);
    bool insert(hashObject && x);
    bool remove(const hashObject & x);
private:
    vector<list<hashObject> > theLists;        //散列链表数组
    int currentSize;

    void rehash();
    size_t myhash(const hashObject & x)const;

};

 

一般对于不使用分离链接的散列表来说，需要解决散列表的冲突问题，而冲突解决方法比较多，但必须让散列表的装填因子低于λ=0.5。因为随着装填因子的增大，散列表的性能出现明显的下降，比如向散列表进行插入操作所需要的探测期望次数呈现指数性增长。因此，散列表的大小需要保持为散列表元素最大个数2倍后的一个素数大小。

当散列表的输入元素个数在不断增大时，需要进行再散列（rehash），依旧保持散列表的大小为元素最大个数2倍后的一个素数大小（而且使用一个相关的新散列函数），以使散列表的装填因子在0.5以下，维持散列表较高的性能。

二.平方探测法

平法探测法的散列表类的代码接口如下 

class hashTable
{
public:
    explicit hashTable(int size=101);

    bool contains(const hashObject & x)const;
    void makeEmpty();
    bool insert(const hashObject & x);
    bool remove(const hashObject & x);

private:
    enum entryType {ACTIVE,EMPTY,DELETED};
    struct hashEntry
    {
        hashObject element;
        entryType info;
        hashEntry(const hashObject & x=hashObject{},entryType i=EMPTY)
            :element{x},info{i}{}
        hashEntry(hashObject && x , entryType i = EMPTY)
            :element{ std::move(x)}, info{ i }{}
    };
    vector<hashEntry> Array;
    int currentSize;
    
    bool isActive(int currentPos)const;
    int findPos(const hashObject & x)const;
    void rehash();
    size_t myhsah(const hashObject & x)const;
};

 

在平法探测法中，散列表的再散列可以用以下多种方法实现，第一种做法是只要表满一半就再散列。第二种做法是只有当插入失败时才进行散列。第三种做法时途中策略（middle of the road strategy）：即当散列表到达某一特定的装填因子时就进行散列。

三.杜鹃散列

杜鹃散列来自于“双选威力（power of two choice）”的概念。在杜鹃散列中，假设有N项元素，保持两个散列表，每个都多于半空，并且有两个散列函数可以将每一项分配到每个表中一个位置，同时保持一项总是被存储在这两个位置中的一个。

杜鹃散列的困难之处在于解决冲突的方法在于用替换逐出的方式，而但当替换逐出的次数较多时，需要尝试选取新的散列函数（再散列）。又当有太多的再散列时则需要对这散列表进行扩张。从而保持散列表的装填因子低于0.5，使散列表保持较高的性能。

杜鹃散列插入解决冲突的代码实现如下

    bool insertHelper1(const AnyType & xx)
    {
        const int COUNT_LIMT = 100;
        AnyType x = xx;
        while (true)
        {
            int lastPos = -1;
            int pos;
            for (int count = 0; cout < COUNT_LIMT; ++count)
            {    
                //在发生冲突时首先尝试用另一散列函数寻找其他位置
                for (int i = 0; i < numHashFunc; i++)
                {
                    pos = myhash(x, i);
                    if (!isActive(pos))
                    {
                        Array[pos] = std::move(hashEntry{ std::move(x),true });
                        ++currentSize;
                        return true;
                    }
                }
            }
            int i = 0;
            do    //没有其他位置可以用时，则替换逐出其他项
            {
                pos = myhash(x, r.nextInt(numHashFunc));
            } while (pos == lastPos && i++ < 5);
            lastPos = pos;
            std::swap(x, Array[pos].element);
        }
        if (++rehash > ALLOWED_REHASHES)
        {
            expand();        //使散列表扩大
            rehash = 0;        
        }
        else rehash();        //保持表大小不变而选新的散列函数的再散列
    }

 

四.跳房子散列

跳房子散列是对经典线性探测算法的改进，通过探测相邻单元使散列表更具有局部性特征。

这种方法的思路是：令MAX_DIST为对最大探测序列所选定的界，对于x项，它比在hash（x）到hash（x）+（MAX_DIST-1)之间的位置上被找到，并设置保留能够指出备选位置上的项是否被散列到位置x的一个元素所占据的信息。

对于跳房子的散列插入x项的操作，先计算出x的散列值，看其位置范围内（hash（x）到hash（x）+（MAX_DIST-1)之间）是否有空位进行插入。否则，顺次找到下一个空位，在空位的散列值减去MAX_DIST处看是否有元素可以顺移下来，否则继续试探下一个位置元素。这操作示意如下图4-1所示，（设MAX_DIST=4，插入项I的散列值为6）

字母对应散列值：(A 7), (B 9), (C 6), (D 7), (E 8), (F 12), (G 11), (H 9), (I 6)

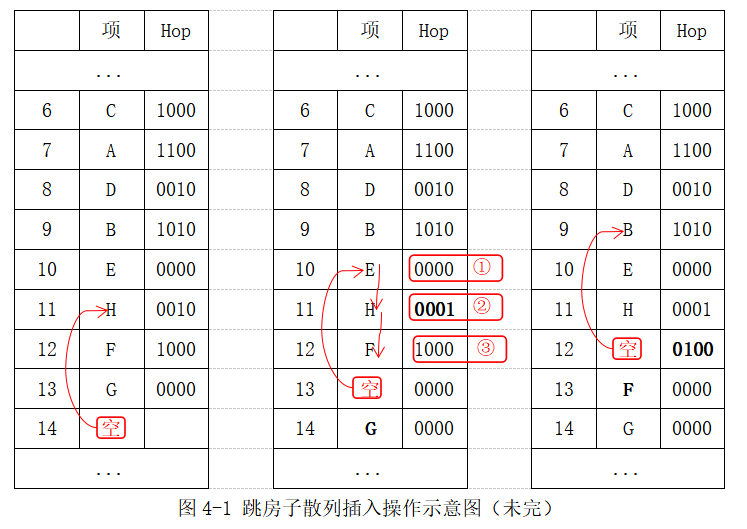
试图插入I（散列值为6），但线性探测到位置14的空位太远；先查阅14-MAX_DIST 位置，即位置11，有G（散列值为11）在13位置（由位置11上的Hop值0010可知），可以向下移动到14位置。

接着13位置为空，先查阅先查阅13-MAX_DIST 位置，即位置10，而位置10上的Hop值0000表示，没有散列值为10的元素，不能进行逐出移动操作。

向下查阅11位置，而位置11上的Hop值0001表示，散列值为11的元素已在最远位置，同样不能进行逐出移动操作。

再向下查阅12位置，位置12上的Hop值1000表示，正好有散列值为12的元素在位置12上，将这元素F向下移动到13位置。

同理，12位置位空，重复上述操作，直到元素 I 在其散列值6到6+MAX_DIST上有空位插入位置，最后的插入示意图如下4-1（续）

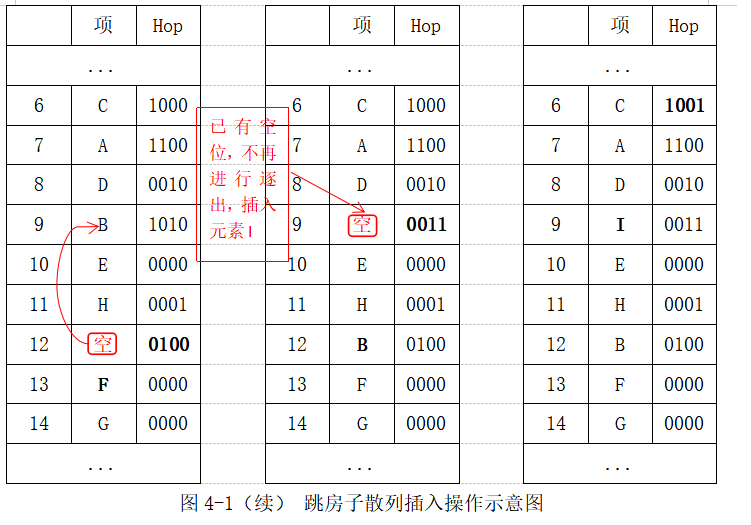
如果在上述的插入操作中，F的散列值是9的话，则插入操作将会被卡住，需要对这散列表进行再散列。

五.通用散列

散列函数簇H={H_a,b(x)=((ax+b)mod p)mod M,其中1<<a<<p-1,0<<b<<p-1,M是散列

表的大小，p是一个比最大的输入关键字还要大的素数且p>M}是通用的。

Mersenne素数像2³-1，2⁵-1，2³¹-1等等，可以通过一次位移和一次减法实现

 

const int DIGS = 31;
const int mersennep = (1 << DIGS) - 1;
int universalHash(int x, int A, int B, int M)
{
    long long hashVal = static_cast<long long>(A)*x + B;
    hashVal = ((hashVal >> DIGS) + (hashVal & mersennep));    // & 位的 于运算
    if (hashVal >= mersennep)
        hashVal -= mersennep;
    return static_cast<int>(hashVal) % M;
}

 

六.可扩散列

可扩散列类似于B树，在插入操作的时候，会引起分裂。

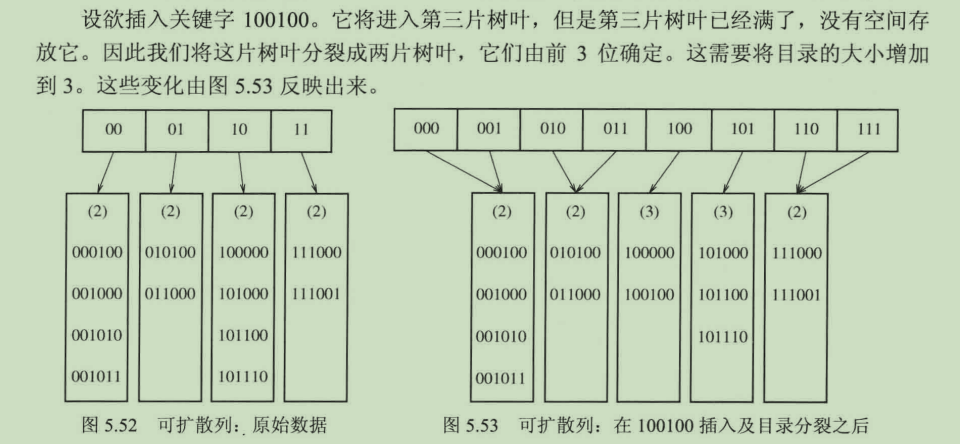
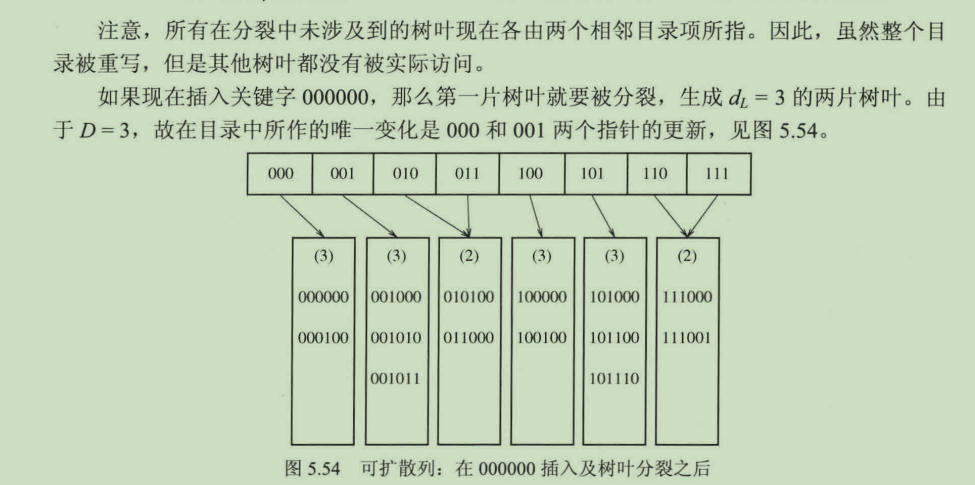
如图5.52的原图，需要按序插入111010，111011，111100。而当最后插入11110的时候，目录的大小须增加到4以区分这叶子上的5个关键字（111000，111001，111010，111011，111100前三位都是111，如果目录的大小为3位，则区分不了这5个关键字，因此需要扩大到4位以区分这5个关键字）。

可扩散列算法的分析结果都是基于合理的假设：位模式（bit pattern）是均匀分布的。

树叶的期望个数为（N/M）log₂e（N 为任一时刻要存储的记录个数，M为一个磁盘区块可以存储的记录个数）。因此，平均树叶满的程度为ln2=0.69。这和B树一样。而目录的期望大小为O(N^1+1/M/M),如果M很小，则目录的可能过大。

这种情况下，可以让树叶包含指向记录的指针而不是实际的记录本身，不过这样的做法会增加一次访问磁盘次数，这对于需要较大存储空间的记录是值得的。