树

数据结构中数组和链表是基本的数据结构，而栈与队列则是建立在数组或链表的基础上且其一端的输入或输出受限的数据结构。

树，则是为了使对数据的平均操作时间缩小到对数级别的又一种基本数据结构。

在树的基础上，为保证最坏情况下或是在庞大的数据需求的情况下也能使平均操作时间趋紧于上述时间界限，对树做优化，进而也衍生出了AVL树、B树等等。

在对这些数据结构做总结的同时并尝试用代码实现一部分数据结构及其操作。

1.二叉查找树的删除节点操作

二叉查找树的删除节点操作分三种情况。一种使删除叶子节点，直接删除即可，一种是该节点只有一个孩子，则调整其父节点的孩子节点为该节点的孩子节点，如图1-1，

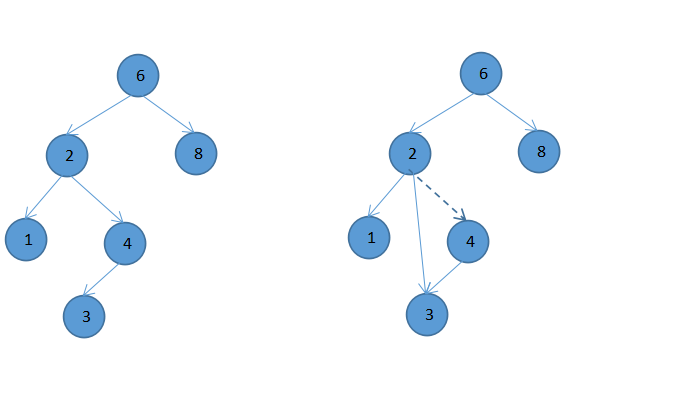
图1-1 删除具有一个孩子的节点（4） 的前后

另一种是节点的左右孩子都存在，那其的删除规则是用该节的右子树的最小节点来代替其位置，然后去删除这最小节点，操作示意图如图1-2

 

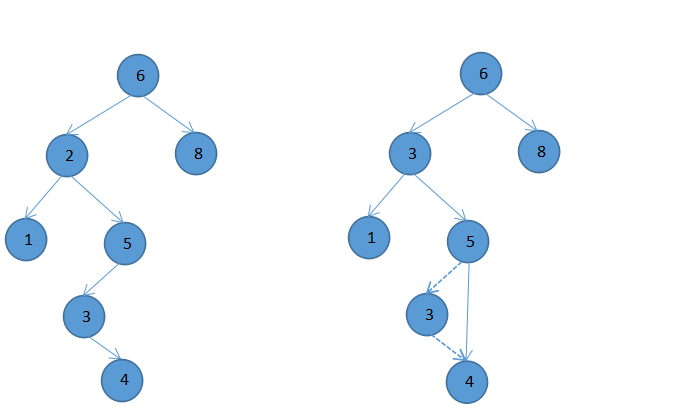
图1-2 删除具有左右孩子节点（2）的前后

通过以上的三种情况的分析，便可对二叉查找树的删除操作进行代码的实现，实现代码如下，

void remove(const Comparable & x, Node *& t)
    {
        if (t == nullptr)
            return;                                                    //对应的节点没有找到，返回即可
        if (x < t->element)
            remove(x, t->left);
        else if (x > t->element)
            remove(x, t->right);
        else if (t->left == nullptr&& t->right == nullptr)            //找到对应节点且具有左右孩子
        {
            t->element = findMin(t->right) - element;
            remove(t->element, t->right);
        }        
        else                                                        //找到对应节点且只具有一个孩子
        {
            Node *oldNode = t;
            t = (t->left != nullptr) ? t->left : t->right;
            delete oldNode;
        }
    }

 

2.AVL树

AVL树是带有平衡条件的二叉查找树，它保证了树的深度是O（logN）。

虽然是一棵理想的平衡树，但其插入和删除操作却要视情况来及时调整树的结构，以使其保持平衡的状态。

然而，这些调整操作的开销相对于糟糕的线性情况查找是值得的。

其插入的平衡调整有四种类型：LL型，RR型，LR型和RL型。

但其中LL型和RR型是对称的，又LR型和RL型是对称的，故可以大致分为两种情况（a点为自下往上首个不平衡点，a的左右子树深度相差大于1）。

LL型调整示意图如下图1-4

图1-4 LL型调整

LR型调整示意图如下图1-5

 

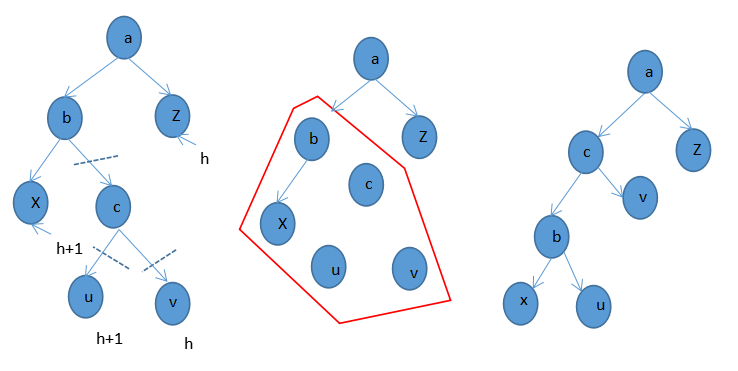
图1-4（1） LR型的调整，先a点的左子树按RR型调整一次

 

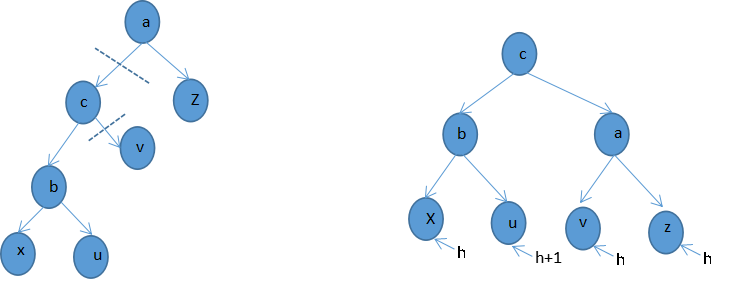
图1-4（2）LR型的调整，再将a点自身按LL型调整一次

相应的调整代码如下：

 

static const int ALLOWED_IMBALANCE = 1;
    void balance(Node * t)
    {
        if (height(t->left) - height(t->right) > ALLOWED_IMBALANCE)
            if (height(t->left->left) >= height(t->left->right))        //LL型
                rotateWithLeftChild(t);
            else                                                        //LR型
                doubleWithLeftChild(t);
        else if (height(t->right) - height(t->left) > ALLOWED_IMBALANCE)
            if (height(t->right->right) >= height(t->right->left))
                rotateWithRightChild(t);                                //RR型
            else
                doubleWithRightChild(t);                                //RL型
    }
    void rotateWithLeftChild(Node *& a)
    {
        Node *b = a->left;            
        a->left = b->right;            //a 的左孩子继承 b 的右孩子
        b->right = a;                    //b 右孩子继承 a
        a->height = max(height(a->left), height(a->right)) + 1;
        b->height = max(height(b->left), a->height) + 1;
        a = b;                        //b 赋值做父节点
    }
    void rotateWithRightChild(Node *& k2)
    {
        Node *k1 = k2->right;
        k2->right = k1->left;
        k1->left = k2;
        k2->height = max(height(k2->left), height(k2->right)) + 1;
        k1->height = max(height(k1->right), k2->height) + 1;
        k2 = k1;
    }
    void doubleWithLeftChild(Node *& k3)    //LR型
    {
        rotateWithRightChild(k3->left);        //先至下而上，k3的左子树（a->left)看成 RR 型调整一次
        rotateWithLeftChild(k3);            //再将 a 自己看成 LL 型调整一次
    }
    void doubleWithRightChild(Node *& k3)
    {
        rotateWithLeftChild(k3->right);
        rotateWithRightChild(k3);
    }

 

LL型和RR型是对称的，又LR型和RL型是对称的，故其的调整做相应的调转即可。

而AVL树节点的删除操作与二叉查找树的删除操作相似，只是AVL树在完成删除操作后，需要做一次平衡调整。

3.B树

B树适用于拥有庞大数量的数据结构，利用这一数据结构中的某个不重复的关键字构造B树，可以大大提高数据的查找效率。同样，在对B树进行相应的插入或删除操作时，需要对B树进行调整，但总的来说这调整的开销对于保持B树访问效率是值得的。

在进行对m阶B树的插入操作时，对于节点关键字到达m个的，自下而上进行分裂，使节点的关键字保持在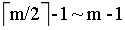之间。

在进行对m阶B树的删除操作时，总的分两种情况：

1.删除的关键字在终端

对于节点内关键字数大于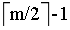的，直接删除；

对于节点内关键字数等于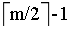的，先用父节点的相邻关键字覆盖要删除的关键字，再向要删除关键字所在节点的兄弟节点相邻借关键字覆盖父节点中选中的关键字，最后删除该兄弟节点的选中关键字；

对于节点内关键字数等于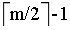，且向左右关键字不足借的，先删除该关键字，再父节点的相邻关键字及其相邻子节点的关键字进行合并，当父节点的关键字数不足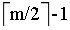，自下而上重复合并操作；

2.删除的关键字不在终端

用相邻关键字取代要删除的关键字，然后再删除这原来的相邻关键字（这删除操作与二叉查找树的删除操作相似，删除非叶节点时，用其相邻的节点覆盖要删除的节点，最后再删除这原来的相邻节点）。