梯度下降
梯度下降
梯度下降是很常用的算法,它可以讲代价函数j最小化,他不仅用于线性回归算法中,也广泛应用于机器学习其他领域,不仅仅可以最小化代价函数,也可以最小化其他函数,在后边课程会记录.
问题描述
我们有一个函数j(θ_0,θ_1)(也许是线性回归的代价函数,也许是其他函数),我们需要一个算法去最小化函数j(θ0,θ1)
梯度下降思路
-
第一步
给定θ_0,θ_1的初始值,(通常将θ_0 和 θ_1 设为0,也可设为其他值) -
第二步
不停的一点点改变θ_0 和 θ_1,来使j(θ_0,θ_1)变小,知道我们找到j(θ_0,θ_1)的最小值或局部最小值
梯度下降数学定义
注意
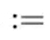
图中:= 为赋值运算,等于计算机中 = 赋值预算符
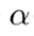
α被称为学习学习率,是个数字,它用来控制梯度下降时,迈出多大的步子,若α值很大,梯度下降会义很大的步子下降,若α很小,梯度下降会以很小的步子下降 如何调整α的值以后会详细记录
为一个导数项,以后会记录
梯度下降正确的流程
梯度下降不正确的流程
错误之处:θ_0已经计算完更新了值,temp1会使用已更新的θ_0来计算导数项,所以此算法并不是用来实现梯度下降的正确算法.同步更新是梯度下降最自然的实现算法,当提到梯度下降时,一般指的就是同步更新的实现算法,若使用图中的不正确的非同步算法,也有可能得到正确值,但并不是人们所指的梯度下降算法,而是具有不同性质的其他算法,我们应该在梯度下降算法中实施真正的实现算法--同步更新
