20172330 2018-2019-1 《程序设计与数据结构》第九周学习总结
20172330 2018-2019-1 《程序设计与数据结构》第九周学习总结
教材学习内容总结
一、无向图:
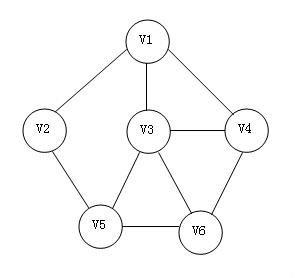
边没有方向的图称为无向图。
-
无向图中,表示边的顶点对是无序的,例如,标记顶点A,B,C,D,一条边可以表示为(A,B)。无向图表示顶点对是无序的,所以边(A,B)意味着A和B之间的连接是双向的,在一个无向图中,(A,B)和(B,A)所代表的边的含义完全一样。
-
含有最多条边的无向图称为完全图:Edges=(n-1)*n/2.

-
如果无向图中任意两个顶点间都有路径,则无向图称为连通的。
-
路径是连接图中两个顶点的边的序列,路径长度为路径所含边的数目(顶点个数减一)
-
第一个顶点和最后一个顶点是同一个顶点且没有重复边的路径,称为一个环。
-
如果图中两个顶点之间有边连接,则称这两个顶点是邻接的(邻居),自己连接到自己的边称为自循环或悬挂。
二、有向图
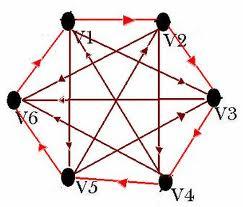
如果给图的每条边规定一个方向,那么得到的图称为有向图,其边也称为有向边。在有向图中,与一个节点相关联的边有出边和入边之分,而与一个有向边关联的两个点也有始点和终点之分。
- 顶点是有序对的图称为有向图,有向图的每条边都带有一个移动方向,这个方向有顶点的顺序指定,所以(A,B)表示只允许从A移动到B,但不允许另一个方向的移动。
- 树就是图,树的大部分工作是针对有向树。有向树是一个有向图。
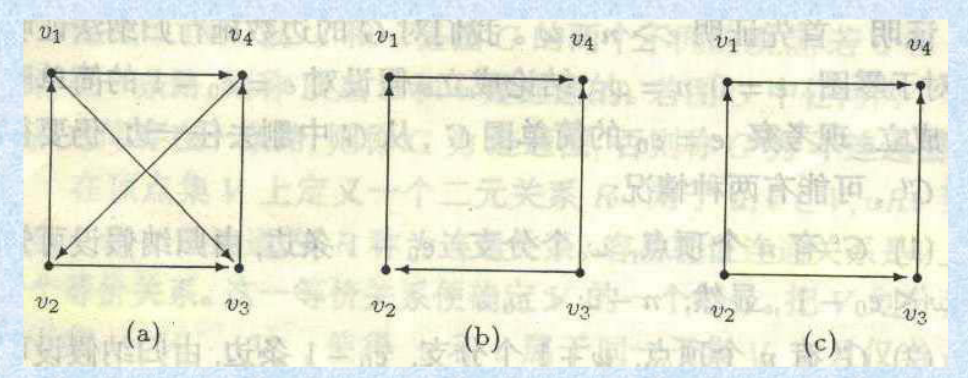
如上图:a是强连通,b是单向连通,c是弱连通。
三、网络
- 网络是一种图,一般认为它专指加权图,是一种每条边都带有权重或代价的图。
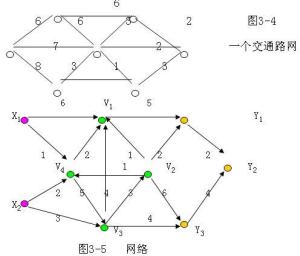
四、常用的图算法
-
遍历
1.深度优先遍历
首先从图中某个顶点v0出发,访问此顶点,然后依次从v0相邻的顶点出发深度优先遍历,直至图中所有与v0路径相通的顶点都被访问了;若此时尚有顶点未被访问,则从中选一个顶点作为起始点,重复上述过程,直到所有的顶点都被访问。可以看出深度优先遍历是一个递归的过程。
2.广度优先遍历
首先,从图的某个顶点v0出发,访问了v0之后,依次访问与v0相邻的未被访问的顶点,然后分别从这些顶点出发,广度优先遍历,直至所有的顶点都被访问完。 -
最小生成树
1.一个连通图的生成树是一个极小的连通子图,它含有图中全部的顶点,但只有足以构成一棵树的n-1条边。我们把构造连通网的最小代价生成树。称为最小生成树。其边的权重总和小于或等于同一个图中其他任何一棵生成树的权重总和。
2.Prim算法:先以一个结点作为最小生成树的第一个结点,然后以迭代的方式找出与最小生成树中各结点权值最小边,加到最小生成树中。加入之后如果产生回路则跳过这条边,选择下一个结点。当所有结点都加入到最小生成树中之后,就找出最小生成树了。

五、图的实现策略
- 邻接表
因为树就是图,所以实现图的最好方式也许是采用实现树已用过的机制。使用一组结点,每个结点包含一个元素及可能和链接其他结点的一个链表。
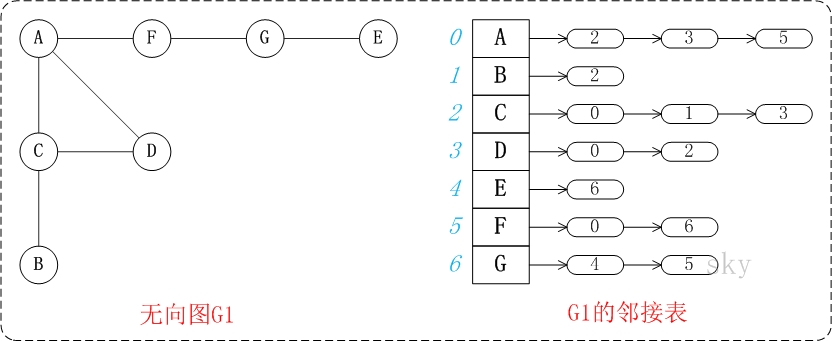
- 邻接矩阵
用一个一维数组存放图中所有顶点数据;用一个二维数组存放顶点间关系(边或弧)的数据,这个二维数组称为邻接矩阵。用邻接矩阵表示图,很容易确定图中任意两个顶点是否有边相连。邻接矩阵分为有向图邻接矩阵和无向图邻接矩阵。对无向图(无向简单图)而言,邻接矩阵一定是对称的,而且对角线一定为零,有向图则不一定如此。
教材学习中的问题和解决过程
-
问题1:图的遍历与树的遍历有什么区别?
-
问题1解决方案:树是有序的,图是无序的。图有两种林子里的方法,一种是广度优先遍历,另一种是深度优先遍历。对于树来说,它的广度优先遍历就是层序遍历,深度优先遍历就是先序遍历。
-
问题2:邻接矩阵有向图与无向图的对比?
-
问题2解决方案:
因为无向图不需要表示整个矩阵,只需给出矩阵对角线的一侧,而有向图的所有边都是定向的,所以结果对应并不相同:
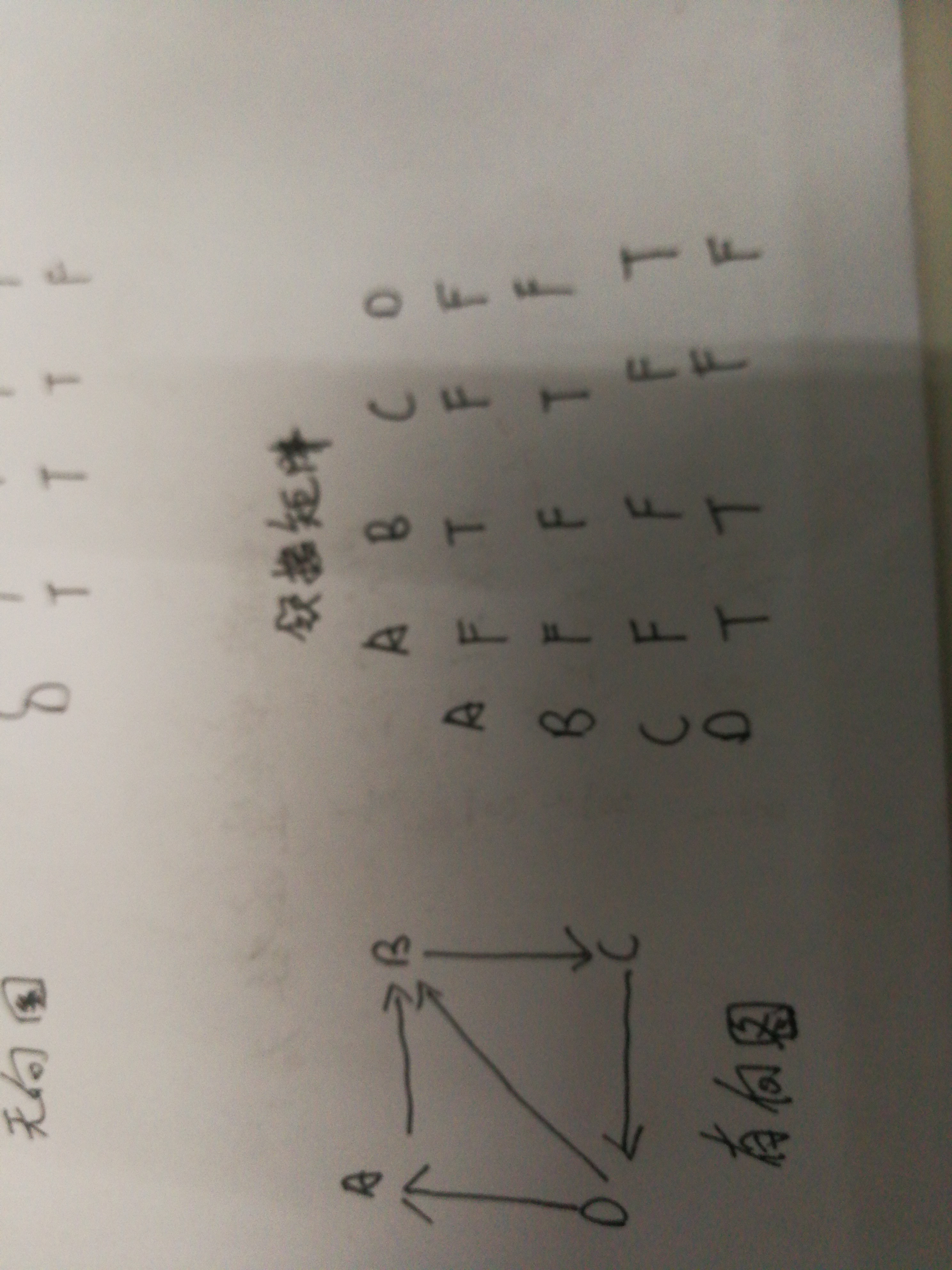

代码调试中的问题和解决过程
- 问题1:暂时无法理解pp15.7
- 问题1解决方案:尚未完成该pp
代码托管

上周考试错题总结
- Since a heap is a binary search tree, there is only one correct location for the insertion of a new node, and that is either the next open position from the left at level h or the first position on the left at level h+1 if level h is full.
A .True
B .Flase
解析:
堆是一棵完全二叉树、不是一颗二叉搜索树。
结对及互评
- 基于评分标准,我给严域俊的博客打分:7分。得分情况如下:
正确使用Markdown语法(加1分)
模板中的要素齐全(加1分)
教材学习中的问题和解决过程, (加3分)
感想,体会真切的(加1分)
点评认真,能指出博客和代码中的问题的(加1分)
- 博客中值得学习的或问题:
- 图片和文字相结合,方便理解。
- 增加了博客中的目录,方便查看,同时样式进行了更新,显得更加美观
- 阅读了许多资料,使得博客更有说服力。
- 代码中值得学习的或问题:
- commit依旧很详细,有条理性。
点评过的同学博客和代码
- 本周结对学习情况
- 20172333
- 结对学习内容
教材第11章,运行教材上的代码
完成课后自测题,并参考答案学习
完成课后自测题,并参考答案学习
完成程序设计项目:至少完成PP11.3、PP11.8
其他(感悟、思考等,可选)
这一周花了点心思在这一章上面,也好好阅读了很多内容,掌握的还算可以。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0/0 | 1/1 | 10/10 | |
| 第二周 | 700/700 | 1/2 | 10/20 | |
| 第三周 | 700/1400 | 1/3 | 10/30 | |
| 第四周 | 500/1900 | 2/5 | 10/40 | |
| 第五周 | 569/2469 | 1/6 | 10/50 | |
| 第六周 | 1070/3539 | 1/7 | 10/60 | |
| 第七周 | 986/4625 | 1/8 | 10/70 | |
| 第八周 | 1023/5648 | 2/10 | 10/80 | |
| 第九周 | 1023/6967 | 1/11 | 10/90 | |
| 参考:软件工程软件的估计为什么这么难,软件工程 估计方法 |
-
计划学习时间:10小时
-
实际学习时间:10小时


