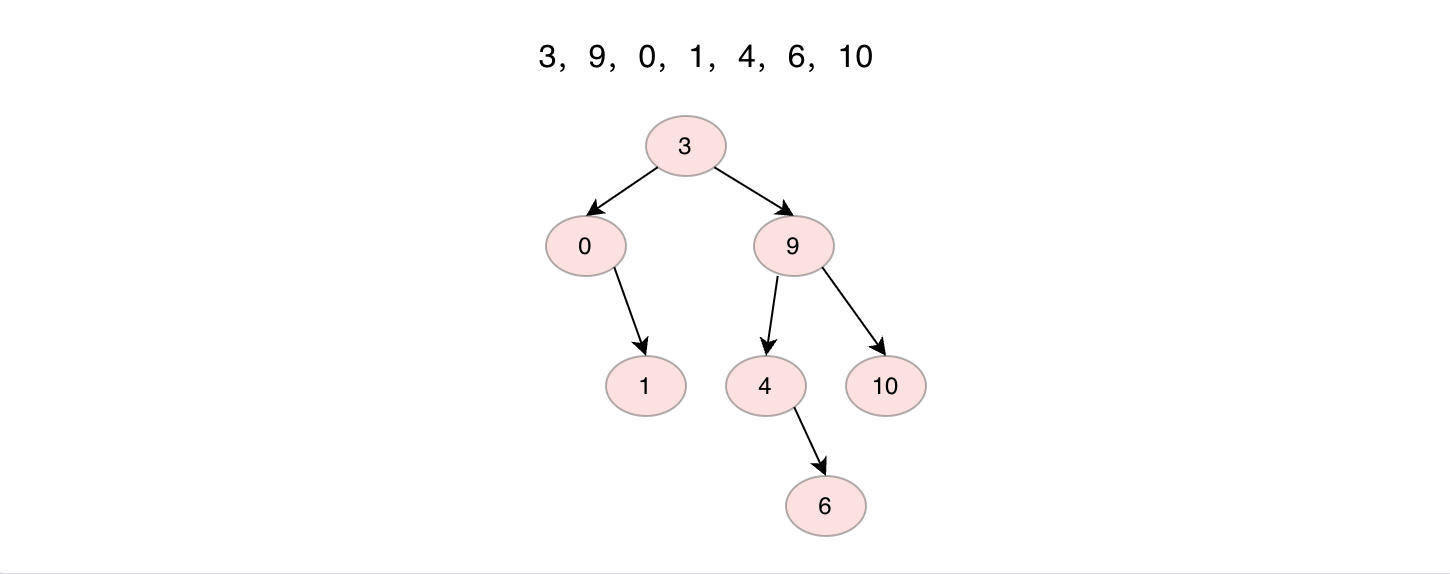
二叉搜索树,一个简单但是非常常见的数据结构
前言
今天leetcode的每日一题450是关于删除二叉搜索树节点的,题目要求删除指定值的节点,并且需要保证二叉搜索树性质不变,做完之后,我觉得这道题将二叉搜索树特性凸显的很好,首先需要查找指定节点,然后删除节点并且保持二叉搜索树性质不变,就想利用这个题目讲讲二叉搜索树。
二叉搜索树作为一个经典的数据结构,具有链表的快速插入与删除的特点,同时查询效率也很优秀,所以应用十分广泛,例如在文件系统和数据库系统一般会采用这种数据结构进行高效率的排序与检索操作。同时因为实现也简单,作为一些公司算法题入门题目也是常有的事情,所以很需要被掌握哦~♥️
所有源码已经放在我的github中,其中包括之前实现算法及每日一题,可以查看Data-Structures-and-Algorithms哦~
性质
二叉搜索树或者是一棵空树,或者是具有下列性质的一棵二叉树,如果当前节点具有左子树,则左子树上的每一个节点值均小于等于当前节点值,如果当前节点具有右子树,则右子树上的每一个节点值均大于等于当前节点值。依据这个性质,当我们前序遍历二叉搜索树的时候,得到的序列应该是从小到大的非递减序列。同时搜索指定值时,只需要与当前节点比较,根据相对大小在左子树或者右子树上进行搜索。
实现
根据二叉搜索树的性质我们接下来需要实现插入节点,查询节点,删除节点功能。
节点结构
public class TreeNode {
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode() {
}
public TreeNode(int val) {
this.val = val;
}
public TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
初始化
这里我们假设所有节点值大于0,初始化一个头节点。ps:对于树,链表这类数据结构,为了使第一个节点操作与其他节点保持一致,方便操作,常见的方法是添加一个额外的头节点,指向第一个节点。
TreeNode head;
private void init() {
//添加一个头节点
head = new TreeNode(-1);
}
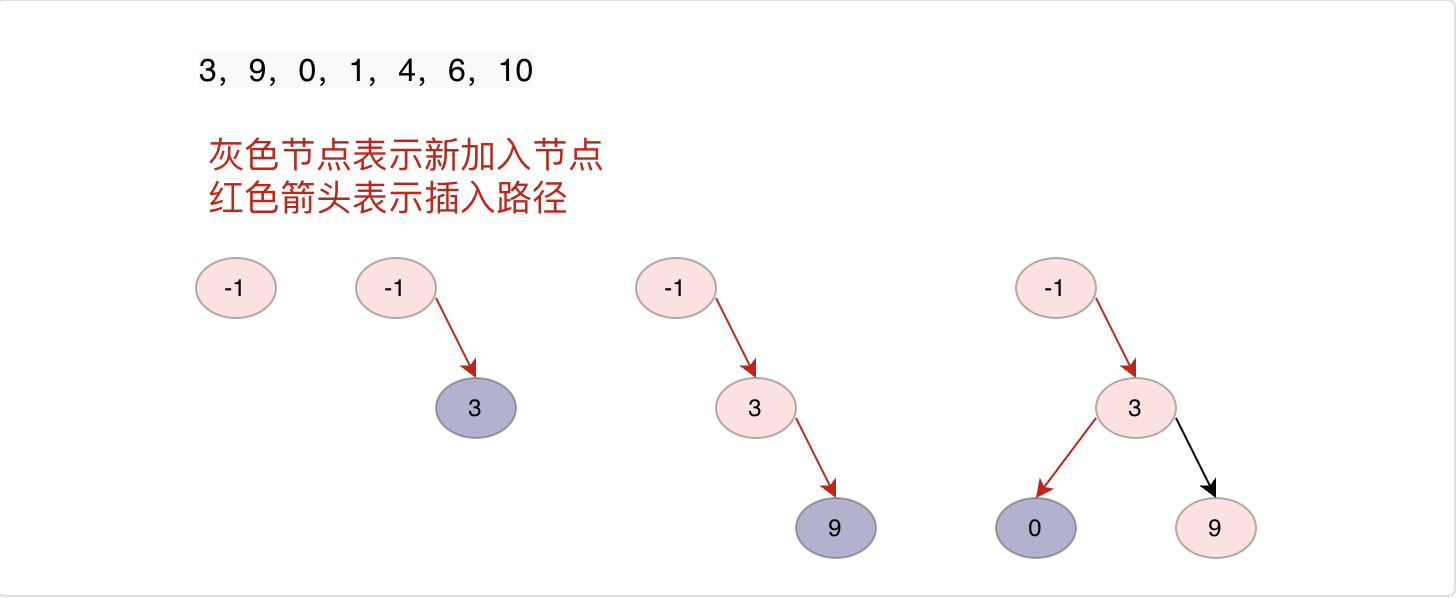
插入节点
从头节点开始我们遍历二叉搜索树,如果当前节点值小于等于插入节点值,则插入节点在当前节点的右子树上,否则在左子树上,一直深度遍历知道当前节点的右子树(左子树)为空,则插入。
/**
* 插入新节点,假设新节点均大于0
* @param val 插入节点值
* @return 插入的节点
*/
public TreeNode insert(int val) {
TreeNode temp = head;
while (true) {
if (temp.val < val) {
//val应该在右子树上
if (null != temp.right) {
temp = temp.right;
continue;
} else {
temp.right = new TreeNode(val);
return temp.right;
}
}
//应该在左子树上
if (null != temp.left) {
temp = temp.left;
continue;
}
temp.left = new TreeNode(val);
return temp.left;
}
}
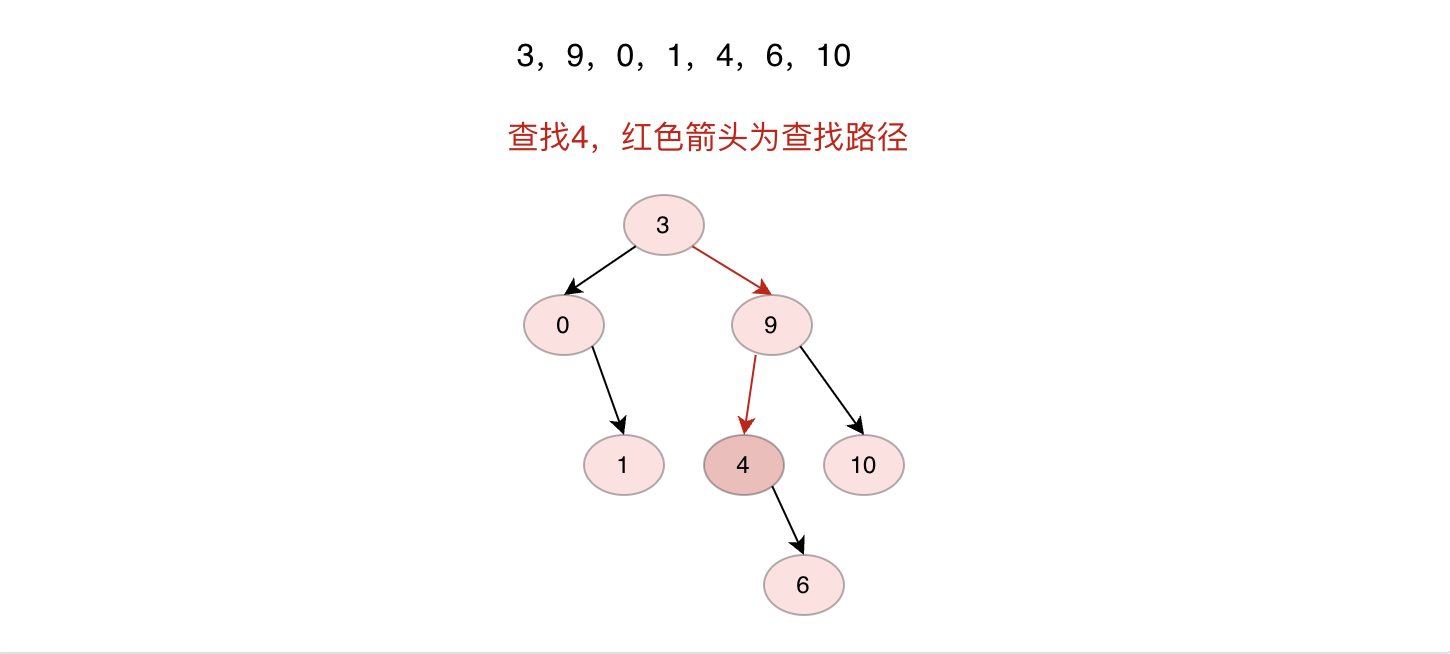
查找节点
查找节点的步骤其实在插入节点的时候已经有体现,其实就是将查找值与当前节点比较,大于当前节点走右子树,小于当前节点走左子树,直到值匹配返回节点,或者没有找到返回null。ps:这里为了后面方便实现删除,同时返回了当前节点以及当前节点的父节点,这里使用了commons-lang3包下的Pair工具。
/**
* 搜索节点值
* @param val
* @return
*/
public Pair<TreeNode, TreeNode> find(int val) {
TreeNode temp = head.right;
TreeNode parent = head;
while (null != temp) {
if (temp.val == val) {
return Pair.of(temp, parent);
}
parent = temp;
if (temp.val < val) {
//在右子树上
temp = temp.right;
continue;
}
temp = temp.left;
}
return null;
}
删除节点
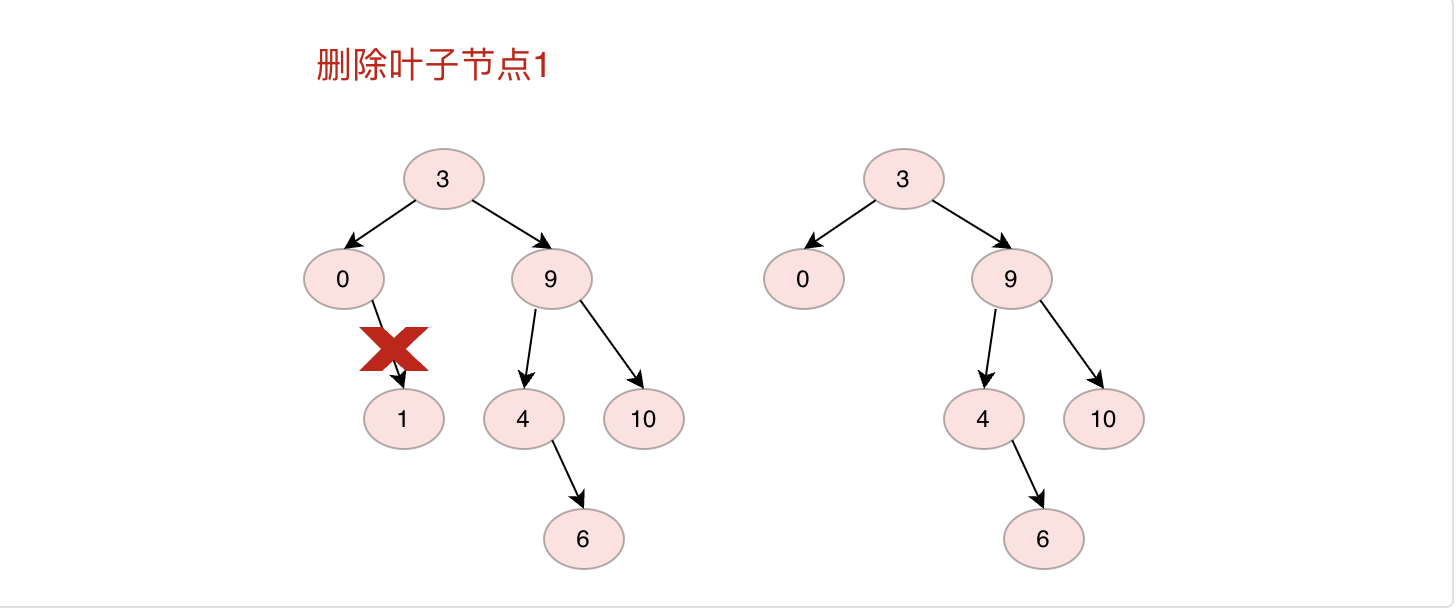
删除节点时候我们需要先找到删除节点的位置,然后做对应操作。有三种情况:
1.如果删除的是叶子节点直接删除
2.如果删除的节点只有左子树或者右子树,则直接将左子树或者右子树节点放在删除节点位置
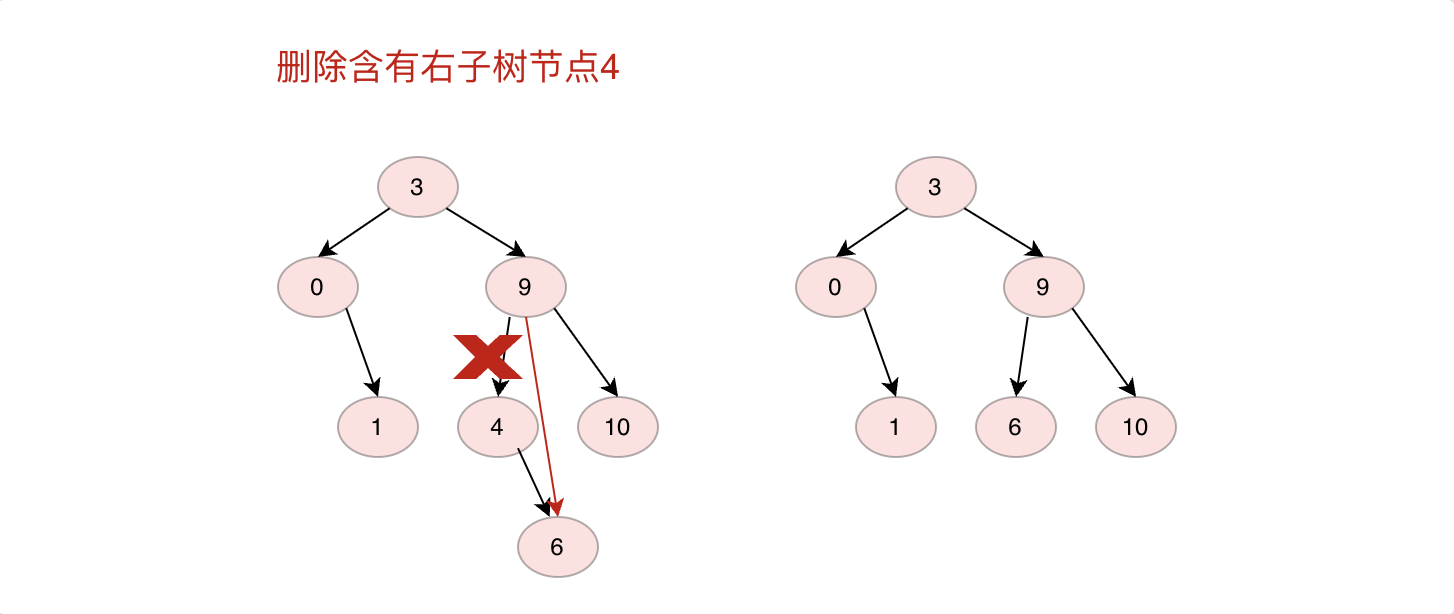
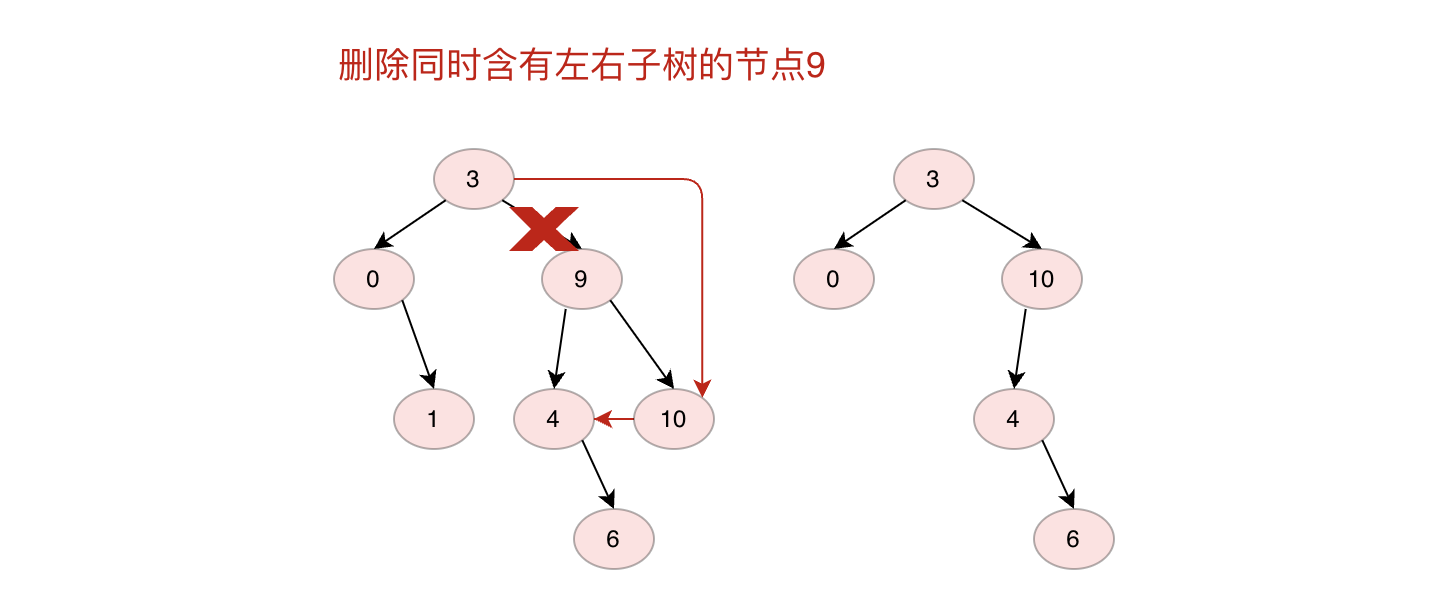
3.如果删除节点同时有左子树和右子树,则将右子树节点放在原来节点位置,将左子树放在右子树最左边节点左子树上(反之将左子树放在原来节点位置,右子树放在左子树最右边节点右子树上也可)
/**
* 1.如果删除的是叶子节点直接删除,
* 2.如果删除的节点只有左子树或者右子树,则直接将左子树或者右子树节点放在删除节点位置
* 3.如果删除节点同时右左子树和右子树,则将右子树节点放在原来节点位置,将左子树放在右子树最左边节点左子树上
* @param val
*/
public void delete(int val) {
//找到删除节点,删除节点父节点
Pair<TreeNode, TreeNode> curAndParent = this.find(val);
TreeNode cur = curAndParent.getLeft();
TreeNode parent = curAndParent.getRight();
//记录删除当前节点后,当前节点位置放置哪个节点
TreeNode changed;
if (null == cur.left && null == cur.right) {
changed = null;
} else if (null != cur.left && null != cur.right) {
TreeNode tempRight = cur.right;
while (null != tempRight.left) {
//找到最左侧节点
tempRight = tempRight.left;
}
tempRight.left = cur.left;
changed = cur.right;
} else if (null != cur.left) {
changed = cur.left;
} else {
changed = cur.right;
}
if (parent.left == cur) {
parent.left = changed;
return;
}
parent.right = changed;
}
最后
二叉搜索树易于实现,思想简单,被广泛应用,平均查找,插入,删除时间均为O(logn),但是在删除或者插入节点的过程中,可能因为数据的特点,使得二叉搜索树极端情况下退化为一棵仅有左子树或者右子树的,这时候就跟普通顺序查找无异,时间复杂度变为O(n),因此后面出现了平衡二叉搜索树,左右子树高度相差不超过1,通过旋转将二叉树高度降低,使得查找、插入、删除在平均和最坏情况下都是O(logn)。比如常见的AVL自平衡二叉搜索树,红黑树等等。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号