最优控制——变分法

 

第一章 最优控制基础

1、一般的最优化问题要最小化的性能指标定义在数域上，而变分问题的性能指标（目标泛函）的定义域是函数的集合。

2、 泛函：从任意定义域到实数域或复数域的映射。泛函的定义域是函数集，值域是数集，也就是说，泛函是从函数空间到数域的一个映射

3、最优控制问题的四个基本元素：状态方程、容许控制、目标集、性能指标

其中状态方程(关于状态变量和控制变量的常微分方程)

 

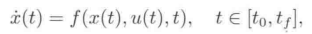
是最优控制问题与经典变分问题的重要区别之一

4、经典变分问题需要连续的控制变量--->之后的极小值原理处理不连续控制变量、状态变量或者控制变量有约束的情况--->更复杂的非线性状态方程、控制变量不可微等      动态规划方法

5、无确定模型的最优控制方法：强化学习与自适应动态规划、模型预测控制、微分博弈、平行控制

第二章 最优控制方法

1、直接变分法 实质：以函数为输入，以实数为输出

在局部范围内对最优解加以”扰动“，再考察性能指标是否发生变化。利用微积分取极限的思想。

（链式法则，先对x求，再对x'求,以及分步积分巴拉巴拉复习一下）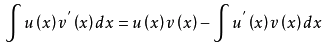

2、拉格朗日的delata方法，加以扰动，对比最优曲线和扰动后的曲线，看新的性能指标是不是会＜最优的，若是极值点，这个增量应该总是>=0的，在该点足够小的邻域内是几乎为0的

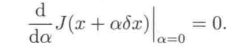
得出

 

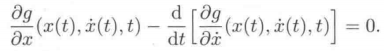
问题：可能导致扰动后x落在定义域之外，结论不再有效

3、拉格朗日乘子法和KKT条件

 

第三章 变分法

1、函数变分：函数的增量 delta x    

泛函增量：J（x+delta x)-J(x)    类比计算极值的时候函数值的差

线性泛函：若满足齐次性条件和可加性条件，则称之为线性泛函

若泛函增量可以写成函数变分的线性泛函及其高阶无穷小项的两部分加和，则称泛函对函数x可微，且其中的线性泛函就是泛函变分。

2、泛函极值的必要条件

驻点条件:泛函变分为0（反证法，前提是定义域是开集） 

适用场景：控制变量可在全空间中任意取值没有约束，容许控制为连续函数全体。

不适用场景：控制变量或其分量取值于实数空间中的闭区间

3、最简变分法：（欧拉-拉格朗日方程）

 

求变分不止可以用看线性泛函和高阶无穷小，还可以用微积分的方法求解：

 

4、 欧拉-拉格朗日方程是关于状态x的二阶微分方程

分为三种情况：

三种结果：

 

5、hamilton方程组

物理学家将欧拉-拉格朗日这个二阶微分方程化成了一阶常微分方程组

6、等式约束的处理

拉格朗日乘子法