LeetCode刷题记录(python3)

由于之前对算法题接触不多,因此暂时只做easy和medium难度的题.

看完了《算法（第四版）》后重新开始刷LeetCode了,这次决定按topic来刷题,有一个大致的方向.有些题不止包含在一个topic中,就以我自己做的先后顺序为准了.

Array

---11.Container With Most Water

给定许多条与y轴平行的直线,求其中两条直线与x轴围成的容器的最大容量.

这道题用到了双指针的思想.我们在数轴的两端分别放置一个left指针和right指针,因为容器容量=较短边*两边位置之差,所以如果移动较大的那个指针,那么容量必定在减小.因此我们不断往中间移动较小的指针才有可能使容量变大,直到两指针相遇为止.

对于算法合理性的逻辑推理:我们假设在best_left和best_right位置取到最大容量,那么left指针到达best_left位置或right指针到达best_right位置至少有一种会发生.不妨令left指针到达best_left位置,此时right指针的位置有三种可能:

1. 位于best_right位置左侧.这说明best_right位置已经被计算过,成立.
2. 位于best_right位置,同上.
3. 位于best_right位置右侧.因为left指针移动的条件是right指针所在边大于left指针所在边,如果符合此条件,且right指针在best_right右侧,那么当前容量一定大于假设中的最大容量,与假设矛盾.所以left指针必定会一路移动至best_right位置.

class Solution(object):
    def maxArea(self, height):
        """
        :type height: List[int]
        :rtype: int
        """
        left = 0
        right = len(height) - 1
        
        most = 0
        while left != right:
            h = min(height[left], height[right])
            most = max(most, h * (right - left))
            if height[left] < height[right]:
                left += 1
            else:
                right -=1
       
        return most

Container With Most Water

---16.3Sum Closest

给定一个数组和一个目标值,找到数组中的三个数,使得这三个数之和与目标值之间的差距最小,返回它们的和.

这题的思路与15题类似,也是利用双指针,只不过判定条件从三个数之和是否为零改成了三个数之和是否比目前已有的closest值更接近目标.

class Solution:
    def threeSumClosest(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: int
        """
        closest = nums[0] + nums[1] + nums[2]
        nums.sort()
        length = len(nums)
        for i in range(length):
            l = i + 1
            r = length - 1
            while l < r:
                tmp = nums[i] + nums[l] + nums[r]
                if tmp == target:
                    closest = target
                    break
                elif tmp < target:
                    if target - tmp < abs(target - closest):
                        closest = tmp
                    l += 1
                elif tmp > target:
                    if tmp - target < abs(target - closest):
                        closest = tmp
                    r -= 1
        return closest

3Sum Closest

 

---18.4Sum

找出list中所有相加等于target的4个数的list.

一开始我的思路是令new_target=target-num1,然后转换为一个3Sum问题,但这种做法的时间复杂度太高了.查看Solution后发现这道题要使用hash的思想,在python中对应的实现就是使用先dict存储list中的两数之和和它们在list中的位置,然后对于这个dict中的value,寻找一个key=target-value,然后将他们对应的数字存入list即可.需要注意的是python中的list,set,dict是不可哈希的,int,float,str,tuple是可哈希的.

class Solution:
    def fourSum(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: List[List[int]]
        """
        d = dict()
        for i in range(len(nums)):
            for j in range(i+1,len(nums)):
                sum2 = nums[i]+nums[j]
                if sum2 in d:
                    d[sum2].append((i,j))
                else:
                    d[sum2] = [(i,j)]
        
        result = []
        for key in d:
            value = target - key
            if value in d:
                list1 = d[key]
                list2 = d[value]
                for (i,j) in list1:
                    for (k,l) in list2:
                        if i!=k and i!=l and j!=k and j!=l:
                            flist = [nums[i],nums[j],nums[k],nums[l]]
                            flist.sort()
                            if flist not in result:
                                result.append(flist)
        return result

 

---35.Search Insert Position

给定一个有序list和一个数target,求这个数在这个list中的位置.

有序,马上想到了二分查找,只不过要针对找不到的情况进行一下特殊处理.普通的二分查找在找不到时返回的是-1,我们这里只要返回找不到时传入函数的left就行了.

class Solution:
    def searchInsert(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: int
        """
        def bs(numlsit, l, r):
            while l <= r:
                mid = int((l + r) / 2)
                if numlsit[mid] == target:
                    return mid
                elif numlsit[mid] < target:
                    return bs(numlsit, mid+1, r)
                else:
                    return bs(numlsit, l, mid-1)
            return l
        
        return bs(nums, 0, len(nums)-1)

 

---41.First Missing Positive

给定一个无序list,求出其中缺失的最小正整数,要求时间复杂度O(n).

设list长度为l的话,最后的答案肯定是1~l+1之间的一个正整数,所以想到了设置标志数组flag,flag[i]为1表示i+1已经出现过了.遍历一次list后再遍历一次flag,遇到的第一个0的index就是答案.如果遍历完整个flag都没有输出值,说明答案是l+1.

class Solution:
    def firstMissingPositive(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        if nums == []:
            return 1
        l = len(nums)
        pi = [0] * l
        for i in range(l):
            tmp = nums[i]
            if tmp > 0 and tmp <= l:
                pi[tmp-1] = 1
        for i in range(l):
            if pi[i] == 0:
                return i+1
        return l+1

 

---45.Jump Game II

给定一个非负整数list,初始位置在list[0],list的值代表了该位置能向前走的最大步数,求走到list末尾所需的最小次数(假设一定能够走到末尾).

既然要求最小次数,那么目的就是每一步都尽可能地往前走.这里的"尽可能"并非是每一步都走能走的最大步数,而是走到的位置加上该位置的最大步数,这代表了我们下一步的选择范围.理清这一点后代码就很简单了.

class Solution:
    def jump(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        l = len(nums)
        pos = 0
        sum = 0

        def find_next(pos):
            next = 0
            pace = nums[pos]
            max = 0
            if pos + pace >= l - 1:
                next = l - 1
            else:
                for i in range(1, pace+1):
                    tmp = i + nums[pos+i]
                    if tmp > max:
                        max = tmp
                        next = pos + i
            return next

        while pos < l - 1:
            pos = find_next(pos)
            sum += 1
            
        return sum

 

---55.Jump Game

给定一个非负整数list,初始位置在list[0],list的值代表了该位置能向前走的最大步数,求是否能走到list末尾.

这道题和45题类似,我们仍然采用45题的走法,但是加入一个判定条件,如果走到了list[i]=0的位置说明不能够走到终点,输出False,否则输出True.

class Solution:
    def canJump(self, nums):
        """
        :type nums: List[int]
        :rtype: bool
        """
        l = len(nums)
        pos = 0
        sum = 0

        def find_next(pos):
            next = 0
            pace = nums[pos]
            max = 0
            if pos + pace >= l - 1:
                next = l - 1
            else:
                for i in range(1, pace + 1):
                    tmp = i + nums[pos + i]
                    if tmp > max:
                        max = tmp
                        next = pos + i
            return next

        while pos < l - 1:
            if nums[pos] == 0:
                return False
            pos = find_next(pos)
            sum += 1

        return True

 

---59.Spiral Matrix II

给定一个正整数n,生成一个n*n的矩阵,其中元素按照螺旋形从1一直到n^2

观察这个生成的矩阵,会发现每一圈都是从左上角开始,沿着顺时针方向递增的规律生成的.按照这个思路,我们定义一个circle函数,它每次都在n*n的矩阵中生成一圈符合条件的数.这个函数接受三个参数,分别代表了出发点,边长还有初始值.其中出发点从(0,0)开始,每次增加(1,1),边长从n开始每次-2,初始值可以通过函数中加入数字的次数得到.

class Solution:
    def generateMatrix(self, n):
        """
        :type n: int
        :rtype: List[List[int]]
        """
        spiral = [[0 for i in range(n)] for j in range(n)]

        def circle(start, length, initial):
            sum = 0
            for i in range(length):
                spiral[start][start+i] = i + 1 + initial
                sum += 1
            for i in range(length-1):
                spiral[start+i+1][start+length-1] = i + length + 1 + initial
                sum += 1
            for i in range(length-1):
                spiral[start+length-1][start+length-i-2] = i + 2 * length + initial
                sum +=1
            for i in range(length-2):
                spiral[start+length-i-2][start] = i + 3 * length - 1 + initial
                sum += 1
            return sum

        times = int((n+1)/2)
        sum = 0
        for i in range(times):
            sum += circle(i, n-2*i, sum)


        return spiral

 

---63.Unique Paths II

给定一个m*n的矩阵,其中0代表可以走的路,1代表障碍物.机器人只能往下或往右走,初始位置在矩阵左上角,求可以让机器人走到矩阵右下角的路径的数量.

一开始想用深度优先遍历解决,后来发现太费时间,于是想到了动态规划.公式如下:

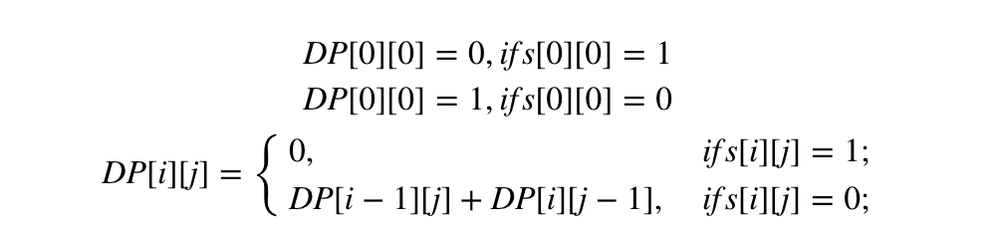
class Solution:
    def uniquePathsWithObstacles(self, obstacleGrid):
        """
        :type obstacleGrid: List[List[int]]
        :rtype: int
        """
        m = len(obstacleGrid)
        n = len(obstacleGrid[0])

        dp = [[0 for i in range(n)] for j in range(m)]

        dp[0][0] = 0 if obstacleGrid[0][0] == 1 else 1

        for i in range(m):
            for j in range(n):
                if obstacleGrid[i][j] == 1:
                    dp[i][j] == 0
                else:
                    if i-1 >= 0:
                        dp[i][j] += dp[i-1][j]
                    if j-1 >= 0:
                        dp[i][j] += dp[i][j-1]

        return dp[m-1][n-1]

 

---64.Minimum Path Sum

给定一个m*n的非负矩阵,矩阵中的数字代表权值,起点在矩阵左上角,只能往右或往下走,求走到矩阵右下角所需的最小路径长度.

基本的动态规划题,dp[0][0]=grid[0][0],dp[i][j]=grid[i][j]+min(dp[i-1][j],dp[i][j-1]),第一排和第一列由于没有上/左的格子,需要提前处理.

class Solution:
    def minPathSum(self, grid):
        """
        :type grid: List[List[int]]
        :rtype: int
        """
        m = len(grid)
        n = len(grid[0])
        dp = [[0 for i in range(n)] for j in range(m)]
        dp[0][0] = grid[0][0]

        for i in range(1,n):
            dp[0][i] = grid[0][i] + dp[0][i-1]

        for i in range(1,m):
            dp[i][0] = grid[i][0] + dp[i-1][0]

        for i in range(1, m):
            for j in range(1, n):
                dp[i][j] = grid[i][j] + min(dp[i-1][j], dp[i][j-1])
        
        return dp[-1][-1]

 

---66.Plus One

给定一个非空的个位数数组,这个数组整体代表了一个非负整数.将这个非负整数+1后用个位数数组的形式返回.

思路比较简单,就是将数组中的数分别取出乘上位数后相加,再将这个数+1后存入另一个数组.值得注意的是python虽然支持大数运算,但如果超出了2^63-1的范围后用int()类型转换会丢失一部分值,所以要在运算过程中转换为字符串来处理.

class Solution:
    def plusOne(self, digits):
        """
        :type digits: List[int]
        :rtype: List[int]
        """
        plus = []
        sum = 0
        l = len(digits)
        for i in range(l):
            sum *= 10
            sum += digits[i]

        sum += 1
        while sum != '' and sum > 0:
            plus.insert(0,sum%10)
            sum = str(sum)[:-1]
            if sum != '':
                sum = int(sum)

        return plus
        

提交过后虽然AC了,但是运算速度较慢,查看了Solution后发现这题应该用加法器的思想来做,有进位则本位置0,保留进位.

class Solution:
    def plusOne(self, digits):
        """
        :type digits: List[int]
        :rtype: List[int]
        """
        p = 1
        for i in range(len(digits), 0 , -1):
            r = digits[i-1] + p
            if r >= 10:
                p = 1
                digits[i-1] = 0
            else:
                p = 0
                digits[i-1] = r
        if p == 1: 
            digits = [1] + digits
        return digits 
                        
        

 

---73. Set Matrix Zeroes

给定一个m*n的矩阵matrix,如果有一个元素是0,则将该元素的所在行和列都变为0.要求in-palce就地操作实现,也就是不使用临时变量,空间复杂度O(1).

空间复杂度O(MN)的解法:新建一个m*n的矩阵,扫描matrix,扫到0就在新矩阵对应行和列赋0,最后把新矩阵赋给matrix

空间复杂度O(M+N)的解法:新建一个长度为M的数组记录每一行是否有0,一个长度为N的数组记录每一列是否有0

空间复杂度O(1)的解法:利用matrix本身记录,首先定义row_flag和column_flag表示矩阵的第一行和第一列是否有0,然后扫描矩阵除了第一行和第一列以外的部分,用第一行和第一列置0来表示有0.

class Solution:
    def setZeroes(self, matrix):
        """
        :type matrix: List[List[int]]
        :rtype: void Do not return anything, modify matrix in-place instead.
        """
        m = len(matrix)
        n = len(matrix[0])
        row_flag = False
        col_flag = False
        for i in range(n):
            if matrix[0][i] == 0:
                row_flag = True

        for i in range(m):
            if matrix[i][0] == 0:
                col_flag = True

        for i in range(1,m):
            for j in range(1,n):
                if matrix[i][j] == 0:
                    matrix[i][0] = 0
                    matrix[0][j] = 0

        for i in range(1,m):
            for j in range(1,n):
                if matrix[i][0] == 0 or matrix[0][j] == 0:
                    matrix[i][j] = 0

        if row_flag:
            for i in range(n):
                matrix[0][i] = 0

        if col_flag:
            for i in range(m):
                matrix[i][0] = 0

 

---74.Search a 2D Matrix

给定一个m*n的整数矩阵,其中每行数从左到右升序排列,并且满足每行的第一个数大于上一行的最后一个数,给定一个target,确定target是否在这个矩阵中.

看见有序还是先想到二分查找,因为每一行之间实际也隐含着顺序了,所以只要先根据每一行的最后一个数判断出我们想要查找的是哪一行,然后对那一行进行二分查找即可.注意[]和[[]]的特殊情况.

class Solution:
    def searchMatrix(self, matrix, target):
        """
        :type matrix: List[List[int]]
        :type target: int
        :rtype: bool
        """
        
        def binary_search(numlist, l, r, t):
            while l <= r:
                mid = int((l + r) / 2)
                if numlist[mid] == t:
                    return True
                elif numlist[mid] < t:
                    return binary_search(numlist, mid+1, r, t)
                else:
                    return binary_search(numlist, l, mid-1, t)
            return False

        if matrix == [] or matrix == [[]]:
            return False
        
        if target < matrix[0][0] or target > matrix[-1][-1]:
            return False


        m = len(matrix)
        n = len(matrix[0])


        for i in range(m):
            if matrix[i][-1] >= target:
                return binary_search(matrix[i], 0, n-1, target)

 

---78.Subsets

给定一个不含重复元素的数组,返回该数组可能的所有子集

一开始想到用递归来做,在list中记录s,然后遍历s中的每个元素i,使用s-i来递归,但是只要数组元素稍微多一点就超时,显然是时间复杂度太高了.

查阅资料后发现这道题应该用回溯法+深度优先遍历,以[1,2,3]为例,第一层元素为[],第二层元素为[1],[2],[3],每深入一层就要删除刚刚加入的元素,直到数组里的元素全部用完后再回溯: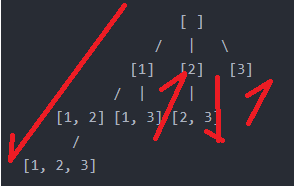

class Solution:
    def subsets(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """        
        l = [[]]


        def dfs(nums, index, path, li):
            for i in range(index, len(nums)):
                li.append(path+[nums[i]])
                path.append(nums[i])
                dfs(nums, i+1, path, li)
                path.pop()

                
        if nums is None:
            return []
        dfs(nums, 0, [], l)
        return l

 

---79.Word Search

给定一个二维list和一个word,判断这个word是否能用二维list中相邻的字母连接而成(不能重复使用)

一道dfs题目,终止条件是当所有字母找完时返回True,当没找完并且四个方向都不能继续走下去时返回False.找到一个字母后分别向四个方向走,如果其中一个方向返回True则整体为True.走过的位置设为'#',当四个方向都回来后将'#'重新变回原来的字母.

class Solution:
    def exist(self, board, word):
        """
        :type board: List[List[str]]
        :type word: str
        :rtype: bool
        """

        m = len(board)
        n = len(board[0])
        l = len(word)

        def near(grid, i, j, word, pos):
            if pos == l:
                return True
            if i-1 < -1 or i+1 > m or j-1 < -1 or j+1 > n or word[pos] != grid[i][j]:
                return False
            tmp = board[i][j]
            board[i][j] = '#'
            res = near(grid, i+1, j, word, pos+1) or near(grid, i-1, j, word, pos+1)\
                  or near(grid, i, j+1, word, pos+1) or near(grid, i, j-1, word, pos+1)
            board[i][j] = tmp
            return res



        for i in range(m):
            for j in range(n):
                if near(board, i, j, word, 0):
                    return True
        return False

 

---80.Remove Duplicates from Sorted Array II

给定一个有序list,使得其中的数字不能重复出现两次以上,要求in-place做法,返回值为处理后的数组的长度

因为要求in-place,所以先用一个for循环找出重复两次以上的数字的位置,将它们改为'#',然后在第二次for循环删去这些'#'.注意这一次的循环要用倒序,否则会因为删去元素导致索引不正确而出错.

class Solution:
    def removeDuplicates(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        if nums == []:
            return 0
        l = len(nums)
        dup = 0
        tmp = nums[0]
        for i in range(1,l):
            if nums[i] == tmp:
                dup += 1
            else:
                dup = 0
                tmp = nums[i]
            if dup >= 2:
                nums[i] = '#'

        for i in range(l-1, -1, -1):
            if nums[i] == '#':
                nums.pop(i)
                
        return len(nums)

        

        

 

---81.Search in Rotated Sorted Array II

给定一个list,是由一个有序数组在某一枢纽处旋转得到的,并且其中可能含有重复元素,要求判断target是否在这个list中.

虽然这个list经过旋转,但是还是可以用二分查找的思想,因为mid的左边或右边一定有一端是有序的.因此只需要在二分查找的时候对此进行判断就行了.另外本题可能有重复值,所以当left,mid和right指向的值都相等时要移动指针来跳出循环.

class Solution:
    def search(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: bool
        """
        left = 0
        right = len(nums)-1

        while left <= right:
            mid = int((left + right) / 2)
            if nums[mid] == target:
                return True

            if nums[mid] < nums[right] or nums[mid] < nums[left]:
                if nums[mid] < target <= nums[right]:
                    left = mid + 1
                else:
                    right = mid - 1
            elif nums[mid] > nums[left] or nums[mid] > nums[right]:
                if nums[mid] > target >= nums[left]:
                    right = mid - 1
                else:
                    left = mid + 1
            else:
                left += 1

        return False

 

---105.Construct Binary Tree from Preorder and Inorder Traversal

给定二叉树的前序遍历和中序遍历,输出该二叉树

前序遍历也就是根-左-右,中序遍历就是左-根-右.我们用递归的方式,preorder[0]必定是根结点,而这个根结点在inorder中的位置的左边是它的左子树,右边是它的右子树.只要抓住这个关键点就可以了.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def buildTree(self, preorder, inorder):
        """
        :type preorder: List[int]
        :type inorder: List[int]
        :rtype: TreeNode
        """
        if len(preorder) == 0:return None
        root_node = TreeNode(preorder[0])
        j = inorder.index(preorder[0])
        root_node.left  = self.buildTree(preorder[1:j+1],inorder[0:j])
        root_node.right = self.buildTree(preorder[j+1:],inorder[j+1:])
        return root_node

 

---106.Construct Binary Tree from Inorder and Postorder Ttaversal

给定二叉树的中序遍历和后序遍历,输出该二叉树

中序遍历是左-根-右,后序遍历是左-右-根.preorder[-1]必定是根结点.然后就和105题类似了.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def buildTree(self, inorder, postorder):
        """
        :type inorder: List[int]
        :type postorder: List[int]
        :rtype: TreeNode
        """
        if len(postorder) == 0:return None
        root_node = TreeNode(postorder[-1])
        j = inorder.index(postorder[-1])
        root_node.left  = self.buildTree(inorder[0:j], postorder[0:j])
        root_node.right = self.buildTree(inorder[j+1:],postorder[j:-1])
        return root_node

 

---119.Pascal's Triangle II

杨辉三角问题,给定k,要求输出杨辉三角的第k行

虽然看似是等腰三角形,但其实我们可以把它看做一个直角三角形,也就是矩阵的下半部分.这题如果用O(k^2)的空间的话非常简单,抓住t[i][j] = t[i-1][j]+t[i-1][j-1]即可.题干给了一个挑战,是用O(k)的空间完成,其实也非常简单,只要设置两个临时变量,分别存储我们要修改的位置的上一层的这一位和前一位即可(逻辑上的上层,实际上只有一维数组).

class Solution:
    def getRow(self, rowIndex):
        """
        :type rowIndex: int
        :rtype: List[int]
        """

        size = rowIndex+1

        tri = [0] * size
        tri[0] = 1

        for i in range(1,size):
            t1 = 1
            for j in range(1,size):
                t2 = tri[j]
                tri[j] = tri[j] + t1
                t1 = t2
        return tri

 

---120.Triangle

给定一个三角形的list,求出从顶到底的最短路径.

经典DP题,非常简单.DP算式为 tri[n-1][i] += min(tri[n][i], tri[n][i+1])

class Solution:
    def minimumTotal(self, triangle):
        """
        :type triangle: List[List[int]]
        :rtype: int
        """

        def dp(tri, n):
            if n < 1:
                return
            for i in range(n):
                tri[n-1][i] += min(tri[n][i], tri[n][i+1])
            dp(tri, n-1)


        dp(triangle, len(triangle)-1)
        return triangle[0][0]

 

---152.Maximum Product Subarray

给定一个list,找出其中一个连续的子数组,使得其中所有数的乘积最大.

首先对整个数组求积,如果大于0则这就是答案,如果小于0则遍历数组,如果找到0则对0左右的数组重复上述操作,如果找到负数则求负数两边的乘积之和.

class Solution:
    def maxProduct(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """

        def product(nums):
            if len(nums) == 0:
                return 0
            s = 1
            for x in nums:
                s *= x
            return s


        def find_max(nums):
            pro = product(nums)
            if pro > 0:
                return pro
            else:
                for i in range(len(nums)):
                    if nums[i] == 0:
                        return max(0, find_max(nums[:i]), find_max(nums[i+1:]))
                    if nums[i] < 0:
                        if len(nums[:i]) > 0:
                            pro_left = product(nums[:i])
                        else:
                            pro_left = pro
                        if len(nums[i+1:]) > 0:
                            pro_right = product(nums[i+1:])
                        else:
                            pro_right = pro
                        pro = max(pro, pro_left, pro_right)
                return pro
        
        
        if len(nums) == 1:
            return nums[0]
        
        pro = find_max(nums)
        return pro



        

 

---153.Find Minimum in Rotated Sorted Array

给定一个排序过的list,在某一结点旋转过,找出其中的最小值

类似81题,还是用二分查找的思想.虽然list被旋转过,但是left-mid和mid-right其中的一段必定是有序的.

class Solution:
    def findMin(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        l = len(nums)
        left = 0
        right = l-1
        mid = (left+right)//2

        while left < right:
            if nums[right] < nums[mid]:
                left = mid+1
            else:
                right = mid
            mid = (left+right)//2

        return min(nums[left], nums[right])

 

---167.Two Sum II - Input array is sorted

给定一个排序过的list,从中找到和等于target的两个数的位置,返回它们以1为起始值的坐标.

双指针的思想,比较简单.值得一提的是,如果需要从无序数组中找到是否有两数之和等于某一target,也是采用先排序再双指针的方法.

class Solution:
    def twoSum(self, numbers, target):
        """
        :type numbers: List[int]
        :type target: int
        :rtype: List[int]
        """
        l = 0
        r = len(numbers) - 1
        while l < r:
            if numbers[l] + numbers[r] > target:
                r -= 1
            elif numbers[l] + numbers[r] < target:
                l += 1
            else:
                break
                
        ans = [l+1, r+1]
        return ans

 

---189.Rotate Array

给定一个list和一个k,使这个list旋转k步

利用python的切片即可

class Solution:
    def rotate(self, nums, k):
        """
        :type nums: List[int]
        :type k: int
        :rtype: void Do not return anything, modify nums in-place instead.
        """
        l = len(nums)
        k = k % l
        nums[:] = nums[l-k:] + nums[:l-k]

 

---209.Minimum Size Subarray Sum

给定一个list和一个正数s,找到list中和大于等于s的最小连续区间的长度.如果没有则返回0.

我的思路是双指针法,用一个滑动的窗口去匹配,如果窗口内的值大于等于s则左移左边框,否则右移右边框,直到右边框到达数组底部并且窗口值小于s位置.

class Solution:
    def minSubArrayLen(self, s, nums):
        """
        :type s: int
        :type nums: List[int]
        :rtype: int
        """
        if sum(nums) < s:
            return 0
        elif max(nums) >= s:
            return 1

        l, r = 0, 1
        add = nums[0] + nums[1]
        minimum = len(nums)

        while l < len(nums):
            if add >= s:
                tmp = r-l+1
                minimum = min(minimum, tmp)
                add -= nums[l]
                l += 1
            else:
                if r < len(nums)-1:
                    r += 1
                    add += nums[r]
                else:
                    break

        return minimum

 

---216.Combination Sum III

给定一个数k和一个数n,要求找到1-9内的k个数,且满足它们的和为n的所有可能组合.

这道题是回溯法的应用.回溯法相当于有剪枝的DFS.思路是:保存当前步骤,如果是一个解就输出;维护状态,使搜索路径（含子路径）尽量不重复.必要时,应该对不可能为解的部分进行剪枝.

• 递归函数的开头写好跳出条件，满足条件才将当前结果加入总结果中
• 已经拿过的数不再拿
• 遍历过当前结点后,为了回溯到上一步,要去掉已经加入到结果list中的当前结点.

代入到这题中,每一个dfs都遍历1-9中当前index后面的数,这确保了已经拿过的数不再拿.进入下一层dfs,并令k-1,n-nums[index],跳出条件是k<0或n<0,满足条件是k==0且n==0.

class Solution:
    def combinationSum3(self, k, n):
        """
        :type k: int
        :type n: int
        :rtype: List[List[int]]
        """
        nums = [1,2,3,4,5,6,7,8,9]
        res = []

        def dfs(nums, k, n, index, path, res):
            if k < 0 or n < 0:
                return
            if k == 0 and n == 0:
                res.append(path)
            for i in range(index, len(nums)):
                dfs(nums, k-1, n-nums[i], i+1, path+[nums[i]], res)

        dfs(nums, k, n, 0, [], res)
        return res

 

---228.Summary Ranges

给定一个有序且无重复数字的list,将其中连续范围的数字合并后返回

根据题意,我们需要确认的其实就是每段连续区间的首尾数字.首数字可能是list的第一个数或是前一个数和它不连续的数,尾数字可能是list的最后一个数或是后一个数和它不连续的数.并且每一个尾数字一定对应着一段连续区间,将这段区间存入一个字符list即可.

class Solution:
    def summaryRanges(self, nums):
        """
        :type nums: List[int]
        :rtype: List[str]
        """
        summary = []
        start = 0
        end = 0
        for i in range(len(nums)):
            if i == 0 or nums[i-1]+1 != nums[i]:
                start = nums[i]
            if i == len(nums)-1 or nums[i+1]-1 != nums[i]:
                end = nums[i]
                if start == end:
                    summary.append(str(start))
                else:
                    summary.append(str(start)+'->'+str(end))

        return summary

 

---229.Majority Element II

给定一个长度为n的list,找到其中出现次数大于[n/3]的所有数.要求时间复杂度O(n),空间复杂度O(1).

我的想法是使用dict存储这个list中每个数出现的次数,然后将其中次数大于[n/3]的存入一个list.但是则不符合空间复杂度的要求.

查阅solution后发现这题可以使用Boyer-Moore多数投票算法解决.这是一种寻找"多数元素"的好方法,基本思想是建立标志位和count,如果匹配到的数字不等于标志位则让count-1,否则count+1,如果count为0时更换标志位.因为本题要求的是出现次数大于[n/3]的所有数,也就是最多可能有两个数,因此要建立两组标志位和count.

class Solution:
    def majorityElement(self, nums):
        """
        :type nums: List[int]
        :rtype: List[int]
        """
        count1, count2, tmp1, tmp2 = 0, 0, 0, 1
        for i in nums:
            if i == tmp1:
                count1 += 1
            elif i == tmp2:
                count2 += 1
            elif count1 == 0:
                tmp1 = i
                count1 = 1
            elif count2 == 0:
                tmp2 = i
                count2 = 1
            else:
                count1 -= 1
                count2 -= 1

        ans = [n for n in (tmp1, tmp2) if nums.count(n) > len(nums) // 3]
        return ans

 

---283.Move Zeroes

给定一个list,将其中所有的0移到末尾,并且保持其他元素的顺序不变.要求in-place完成.

如果我们采用的是交换位置或是移动0的话,index的变化将非常繁琐.所以我们将思路放在非零元素上:总是将非零元素与第一个零元素交换位置,每一次交换后将对应第一个零元素的index+1即可.

 

Dynamic Programming

---95.Unique Binary Search Trees II

给定一个数字n,生成所有存储了1~n的二叉查找树的可能形式.

这题的思路是每次选取一个结点作为根,然后根据这个根把树切分为左右两个子树,再在左右两个子树里选取结点作为根,直至子树为空.注意子树为空时要返回[None]而不是[],否则循环无法进行.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def generateTrees(self, n):
        """
        :type n: int
        :rtype: List[TreeNode]
        """
        def dfs(nums):
            if not nums:
                return [None]
            result = []
            for i in range(len(nums)):
                for l in dfs(nums[:i]):
                    for r in dfs(nums[i+1:]):
                        node = TreeNode(nums[i])
                        node.left, node.right = l, r
                        result.append(node)
            return result

        nums = list(range(1,n+1))
        if n == 0:
            return []
        return dfs(nums)
        
 
        

 

---198.House Robber

给定一个list,代表一条街道上每栋房子里的财物.我们要尽可能多地抢这些财物,但是不能抢相邻的两栋房子.

递推式是:

1. f(0)=nums[0]
2. f(1)=max(nums[0], nums[1])
3. f(k)=max(f(k-1), f(k)+f(k-2))

class Solution:
    def rob(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        if not nums:
            return 0
        elif len(nums) == 1:
            return nums[0]
        else:
            nums[1] = max(nums[0], nums[1])
            for i in range(2,len(nums)):
                nums[i] = max(nums[i]+nums[i-2], nums[i-1])

        return nums[-1]

 

---213.House Robber II

给定一个list,代表一条街道上每栋房子里的财物.我们要尽可能多地抢这些财物,但是不能抢相邻的两栋房子.这个街道是环形的.

这题和198很像,区别只是增加了一个第一栋房子与最后一栋房子不能同时抢的判定.所以我们分为两种情况,同时为了节省空间,采用了临时变量:

1. 抢了第一栋房子,此时问题变为198题的求0~N-1
2. 没有抢第一栋房子,此时问题变为198题的求1~N

class Solution:
    def rob(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        if not nums:
            return 0
        elif len(nums) < 4:
            return max(nums)
        else:
            pplast, plast = 0, 0
            for i in nums[:-1]:
                tmp = plast
                plast = max(pplast+i, plast)
                pplast = tmp
            result = plast
            pplast, plast = 0, 0
            for i in nums[1:]:
                tmp = plast
                plast = max(pplast+i, plast)
                pplast = tmp
            return max(result, plast)

　

---264.Ugly Number II

找到第n个ugly number(质因数只有2,3,5的数字,包括1)

因为ugly number的质因数只有3种可能性,所以每一个ugly number一定是由另一个ugly number乘上这三个数的其中之一得到的(1除外).所以想到了设立3个标志位,分别代表2,3,5的乘数在数组中的位置,判断它们的乘积最小者就是下一个ugly number.

class Solution:
    def nthUglyNumber(self, n):
        """
        :type n: int
        :rtype: int
        """
        ugly = [1]
        tmp_2, tmp_3, tmp_5 = 0, 0, 0



        for i in range(1,n):
            tmp = min(2*ugly[tmp_2], 3*ugly[tmp_3], 5*ugly[tmp_5])
            if tmp == 2*ugly[tmp_2]:
                tmp_2 += 1
            if tmp == 3*ugly[tmp_3]:
                tmp_3 += 1
            if tmp == 5*ugly[tmp_5]:
                tmp_5 += 1
            ugly.append(tmp)
            
        return ugly[-1]

 

---279.Perfect Squares

给定一个正整数n,找到相加之和等于它所需的完全平方数的最小个数.

只要找到表达式dp[i]=min(dp[i],dp[i-j*j])就可以了.

class Solution:
    def numSquares(self, n):
        """
        :type n: int
        :rtype: int
        """
        if n == 0:
            return 0
        dp = list(range(0,n+1))
        dp[1] = 1
        for i in range(1,n+1):
            j = 1
            while j*j <= i:
                dp[i] = min(dp[i], dp[i-j*j]+1)
                j += 1

        return dp[-1]

 

---300.Longest Increasing Subsequence

给定一个无序list,找出其中最长的递增子序列

dp的思路是比较容易想到的,使用一个dp数组存储该位置的递增子序列长度,dp[0]=1,对于i,遍历所有小于i的j,只要nums[j]<nums[i],就使用表达式dp[i]=max(dp[i], dp[j]+1)来更新dp数组. 时间复杂度是O(n^2)

class Solution:
    def lengthOfLIS(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        l = len(nums)
        if l < 2:
            return l
        dp = [1 for i in range(l)]
        for i in range(l):
            tmp = nums[i]
            for j in range(i):
               if nums[j] < tmp:
                   dp[i] = max(dp[i], dp[j]+1)
        return max(dp)

另一种在评论区看到的思路是使用一个tails数组,它的第i位代表的是nums中长度为i的递增子序列的最小数值.易得tails是一个递增数组.然后对于每一个数x,如果它比tails[-1]大,就在tails数组中增加一位,如果它满足tails[i-1] < x <= tails[i],就更新tails[i]=x.这样做的好处是可以用二分查找来确定x的位置.这种做法的时间复杂度是O(nlogn)

def lengthOfLIS(self, nums):
    tails = [0] * len(nums)
    size = 0
    for x in nums:
        i, j = 0, size
        while i != j:
            m = (i + j) / 2
            if tails[m] < x:
                i = m + 1
            else:
                j = m
        tails[i] = x
        size = max(i + 1, size)
    return size

 

---309.Best Time to Buy and Sell Stock with Cooldown

给定一个list代表股票价格,要求卖完股票后的第一天不能买入股票,求买卖可以产生的最大利润.

一开始没有思路,在discuss看到这其实是一道状态转移的问题.总共有hold,notHold,cooldown三种状态,它们之间的转移方程如下:

1. hold---不操作---hold
2. hold---卖股票---cooldown
3. notHold---不操作---notHold
4. notHold---买股票---hold
5. cooldown---不操作---notHold

初始状态是notHold,然后只要遍历prices的list即可.

class Solution:
    def maxProfit(self, prices):
        """
        :type prices: List[int]
        :rtype: int
        """
        hold = float('-inf')
        notHold = 0
        cooldown = float('-inf')
        for p in prices:
            hold = max(hold, notHold-p)
            notHold = max(notHold, cooldown)
            cooldown = hold+p

        return max(notHold, hold, cooldown)

 

---322.Coin Change

给定一个list代表不同面值的钱,和一个总数amount,求出能凑出amount所需的钱的最小数量,如果凑不齐则返回-1.

找到表达式dp[i]=min(dp[i-coin]+1),注意凑不齐的金额设为float('inf')即可.

class Solution:
    def coinChange(self, coins, amount):
        """
        :type coins: List[int]
        :type amount: int
        :rtype: int
        """
        MAX = float('inf')
        dp = [0] + [MAX] * amount

        for i in range(1, amount + 1):
            dp[i] = min([dp[i - c] if i - c >= 0 else MAX for c in coins]) + 1

        return [dp[amount], -1][dp[amount] == MAX]
        

 

---338.Counting Bits

给定一个非负整数num,对于0<=i<=num,返回一个list,代表i的二进制表示中1的数量.

只有0对应的二进制的1的数量是0,对于任意的正整数num,都可以写成num = 2**i + k(k<num/2)的形式,如果k=0时对应的1的数量为1,否则就是1+dp[k].因为k<2**i,所以我们可以确保dp[k]一定已经存过数字.

class Solution:
    def countBits(self, num):
        """
        :type num: int
        :rtype: List[int]
        """
        dp = [0] * (num+1)

        carry = 1
        for i in range(1, num + 1):
            if carry*2 == i:
                carry = i
            dp[i] = 1+dp[i-carry]

        return dp

 

---343.Integer Break

给定一个正整数n,将它拆分成至少两个数字的和,使得这些数字之积最大.

我想到的是dp的做法,dp[n]为n对应的最大积,那么dp[2]=1,dp[n]=max(i*dp[n-i],i*(n-i))

class Solution:
    def integerBreak(self, n):
        """
        :type n: int
        :rtype: int
        """
        dp = [0]*(n+1)
        dp[0] = 1
        dp[1] = 1
        for i in range(n+1):
            for j in range(i):
                dp[i] = max(dp[i], j*(i-j), j*dp[i-j])

        return dp[-1]

实际上这题通过数学推导,可以发现最好的就是将数字三等分,如果不行就二等分,这样就可以很快求解了.

 

Tree

---94.Binary Tree Inorder Traversal

给定一棵二叉树,返回它的中序遍历结果.

递归,如果root为空则返回,否则递归遍历左结点,存入根结点,递归遍历右结点.

如果不用递归的话,可以采用栈来实现,也就是结点非空时就将根结点存入栈,然后进入左结点,直到结点为空时,从栈中弹出第一个结点加入res[],然后访问该结点的右结点.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None


class Solution:
    def inorderTraversal(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        node = []
        def it(root):
            if root == None:
                return
            else:
                it(root.left)
                node.append(root.val)
                it(root.right)
        it(root)
        return node

 

---100.Same Tree

给定两棵二叉树,判断它们是否相同.

递归,如果p与q都存在的话,返回对p与q的val是否相等的判断结果and对p.left和q.left的判断结果and对p.right和q.right的判断结果.如果p与q不存在的话,则用p==q判断是否两者都为None.这里用到的技巧是True and False = Flase.

这题也可以用栈来实现.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def isSameTree(self, p, q):
        """
        :type p: TreeNode
        :type q: TreeNode
        :rtype: bool
        """
        if p and q:
            return p.val == q.val and self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right)
        else:
            return p == q

 

---103.Binary Tree Zigzag Level Order Traversal

给定一棵二叉树,返回它的zigzag遍历结果.(也就是同一层从左到右,下一层再从右到左,如此循环)

我的方法是设立标志位i代表第i层,如果结点存在,且res数组的长度小于i,就在res数组中加入一个[],然后将这个结点的值存入,并递归左结点和i+1,然后递归右结点和i+1.最后再将res中的偶数list做reverse操作.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def zigzagLevelOrder(self, root):
        """
        :type root: TreeNode
        :rtype: List[List[int]]
        """
        res = []
        def helper(root, i):
            if root:
                if len(res) < i:
                    res.append([])
                res[i-1].append(root.val)
                helper(root.left, i+1)
                helper(root.right, i+1)
        
        helper(root,1)
        for i in range(len(res)):
            if i % 2 != 0:
                res[i].reverse()
        return res
            
        

 

---107.Binary Tree Level Order Traversal II

给定一棵二叉树,返回它自底向上,从左到右的遍历结果.

与103题类似,只不过最后是对整个res做reverse操作.

如果不用递归的话,还可以用dfs+栈或bfs+队列.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def levelOrderBottom(self, root):
        """
        :type root: TreeNode
        :rtype: List[List[int]]
        """
        res = []
        def helper(root, i):
            if root:
                if len(res) < i:
                    res.append([])
                res[i-1].append(root.val)
                helper(root.left, i+1)
                helper(root.right, i+1)
        
        helper(root,1)
        res.reverse()
        return res

 

---110.Balanced Binary Tree

 给定一棵二叉树,判断它是不是一棵平衡二叉树.

平衡二叉树的定义:要么是一棵空树,要么左右子树都是平衡二叉树,并且左右子树的深度之差的绝对值不超过1.

如果采用求深度的方法,那么部分结点会被重复访问很多次,所以想到了后序遍历,它的特点是访问到根结点时,根结点对应的左结点和右结点都已经被访问过了.如果在访问过程中发现左结点和右结点的深度之差大于1,就返回-1,同理如果左结点和右结点的返回值已经是-1了,也返回-1,不然就返回1+左结点和右结点的较大值.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def isBalanced(self, root):
        """
        :type root: TreeNode
        :rtype: bool
        """
        
        def helper(root):
            if not root:
                return 0
            left = helper(root.left)
            right = helper(root.right)
            if left == -1 or right == -1 or abs(left-right) > 1:
                return -1
            return 1 + max(left, right)
        
        return helper(root) != -1

 

---111.Minimum Depth of Binary Tree

给定一棵二叉树,返回它的最小深度

递归解决,对于一棵二叉树的每一个结点,如果它同时有左右子树,那么深度为1+min(left,right),否则深度为另一个子树的最小深度+1.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def minDepth(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        
        if not root:
            return 0
        
        if not root.left:
            return 1 + self.minDepth(root.right)
        elif not root.right:
            return 1 + self.minDepth(root.left)
        else:
            return 1 + min(self.minDepth(root.left), self.minDepth(root.right))

        

 

---112.Path Sum

给定一棵二叉树和一个sum,判断二叉树中是否有一条从根结点到叶子结点的路径,使得结点之和等于sum.

比较简单,使用一个辅助值tmp记录路径的和,如果为叶子结点且路径和加上值等于sum则返回True,否则返回helper(root.left) or helper(root.right)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def hasPathSum(self, root, sum):
        """
        :type root: TreeNode
        :type sum: int
        :rtype: bool
        """
        
        def helper(root, sum, tmp):
            if not root:
                return False
            tmp += root.val
            if not root.left and not root.right and tmp == sum:
                return True
            else:
                return helper(root.left, sum, tmp) or helper(root.right, sum, tmp)
            
        return helper(root, sum, 0)

 

---113.Path Sum II

给定一棵二叉树和一个sum,找出所有满足和等于sum的根结点到叶子结点的路径.

思路和112题大体一致,只不过需要在函数中加入两个list参数,一个存储路径,最后如果判断等于sum就加入到另一个中作为最后结果.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def pathSum(self, root, sum):
        """
        :type root: TreeNode
        :type sum: int
        :rtype: List[List[int]]
        """
    
        def dfs(root, sum, ls, res):
            if not root.left and not root.right and sum == root.val:
                ls.append(root.val)
                res.append(ls)
            if root.left:
                dfs(root.left, sum-root.val, ls+[root.val], res)
            if root.right:
                dfs(root.right, sum-root.val, ls+[root.val], res)
                
        if not root:
            return []
        res = []
        dfs(root, sum, [], res)
        return res

 

---114.Flatten Binary Tree to Linked List

给定一棵二叉树,将它变为链表,要求in-place操作

在对根结点操作时,如果已经将它的左右子树都拉平过,就将左子树加入到根结点和右子树中间,所以采用后序遍历顺序来递归.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def flatten(self, root):
        if not root:
            return
        if root.left:
            self.flatten(root.left)
        if root.right:
            self.flatten(root.right)
        left = root.left
        right = root.left
        while right and right.right:
            right = right.right
 
        if right:
            right.right = root.right
        if left:
            root.right = left
        root.left = None

 

---129.Sum Root to Leaf Numbers

给定一棵二叉树,每一个结点都是0-9中的一位数字,求所有根结点到叶子结点的路径上的数字之和.

递归,每深入一个结点就让当前的值*10传下去,直到叶子结点后将值存入一个list,最后对该ist求和即可.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def sumNumbers(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
    
        def helper(root, value, res):
            if root:
                helper(root.left, root.val+value*10, res)
                helper(root.right, root.val+value*10, res)
                if not root.left and not root.right:
                    res.append(root.val+value*10)
        
        if not root:
            return 0
        else:
            res = []
            helper(root, 0, res)
            return sum(res)

 

---144.Binary Tree Preorder Traversal

给定一棵二叉树,返回前序遍历

递归的方法非常简单,这里用栈的方法,创建两个list,pre用于保存最后的结果,stack用于保存过程中的结点.如果栈里还有结点,首先将这个结点出栈,存入pre,然后将这个结点的右结点和左结点存入栈中.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def preorderTraversal(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        pre = []
        stack = [root]
        while stack:
            node = stack.pop()
            if node:
                pre.append(node.val)
                stack.append(node.right)
                stack.append(node.left)
        return pre

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def preorderTraversal(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        def helper(root, prelist):
            if root:
                prelist.append(root.val)
                helper(root.left, prelist)
                helper(root.right, prelist)
            
        prelist = []
        helper(root, prelist)
        return prelist
            

 

---199. Binary Tree Right Side View

给定一棵二叉树,想象你站在这颗二叉树的右边,从上到下给出你能在这棵树上看到的值.

定义一个数组view和一个辅助函数,它的功能是从右到左遍历这颗树,并且当遍历到的结点深度等于当前view的长度时,表明这是该层最右边的结点,将它加入view数组,然后遍历这个结点的右子结点和左子结点.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def rightSideView(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        
        def helper(root, depth):
            if root:
                if depth == len(view):
                    view.append(root.val)
                helper(root.right, depth+1)
                helper(root.left, depth+1)
                
        view = []
        helper(root, 0)
        return view
                
            
        

 

---222. Count Complete Tree Nodes

给定一棵完全二叉树,求结点数

首先定义一个辅助函数get_depth用于求一颗完全二叉树的深度,然后开始构造主函数.如果不存在结点则返回0,否则分别求当前结点的左子树深度和右子树深度.如果左子树深度等于右子树深度,说明左子树是满二叉树,那么只需用深度求出左子树的结点数,然后再对右子树求结点数即可.如果左子树深度不等于右子树深度,那么说明右子树是满二叉树,同理.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def countNodes(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        
        def get_depth(root):
            depth = 0
            while root:
                root = root.left
                depth += 1
            return depth
        depth = get_depth(root)
        
        if not root:
            return 0
        left_depth = get_depth(root.left)
        right_depth = get_depth(root.right)
        if left_depth == right_depth:
            return pow(2, left_depth) + self.countNodes(root.right)
        else:
            return pow(2, right_depth) + self.countNodes(root.left)

 

---226.Invert Binary Tree

翻转二叉树

很简单的一道题.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def invertTree(self, root):
        """
        :type root: TreeNode
        :rtype: TreeNode
        """
        if root:
            tmp = root.right
            root.right = root.left
            root.left = tmp
            self.invertTree(root.left)
            self.invertTree(root.right)
        return root

 

---337.House Robber III

给定一棵二叉树,其中结点的值代表财产,小偷不能偷两个相连的结点,求小偷能偷到的最大财产价值.

这种要维护状态的题首先想到递归,用一个大小为2的一维数组res,res[0]表示不包含当前结点的最大值,res[1]表示包含当前结点的最大值.开始递归,如果该结点不存在则返回[0,0],否则left_val等于左结点的递归调用,right_val等于右结点的递归调用,注意这两个val实际上都是一个和res大小相同的数组.不包含该结点的话,res[0]=max(left_val)+max(right_val),包含该结点的话,res[1]=root.val+left_val[0]+right_val[0].

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def rob(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        def helper(root):
            if not root:
                return [0,0]
            else:
                left_val = helper(root.left)
                right_val = helper(root.right)
                res = [0,0]
                res[0] = max(left_val) + max(right_val)
                res[1] = root.val + left_val[0] + right_val[0]
                return res

        return max(helper(root))

 

Hash Table

---187.Repeated DNA Sequences

DNA是由A,C,G,T四种核苷酸构成的,设计一种算法,能够找到一个DNA里所有重复出现过的长度为10的核苷酸序列.

使用python的dict构造哈希表,用i遍历DNA序列s的第一位到倒数第十位,s[i:i+10]就可以遍历其中所有长度为10的序列.如果在dict中存在这个序列且值等于1(代表出现次数),就将它加入到output的list中,且将值加1.否则将该序列加入dict中,且令值等于1.

class Solution:
    def findRepeatedDnaSequences(self, s):
        """
        :type s: str
        :rtype: List[str]
        """
        sub = {}
        output = []
        for i in range(len(s)-9):
            temp = s[i:i+10]
            if temp in sub:
                if sub[temp] == 1:
                    sub[temp] += 1
                    output.append(temp)
            else:
                sub[temp] = 1
                
        return output

 

---205. Isomorphic Strings

给定两个字符串s和t,判断它们是不是同构的.同构是指,将其中一个字符串中的相同字符用另一个字符替换,如果这个字符串可以变为另一个字符串,则称他们是同构的.

这题我的思路是分别遍历s和t,用两个dict存储结果.如果其中已经有了遍历到的字符,就令值加1,否则添加该字符,然后用dict.values()进行比较即可.但是提交后出现了错误.思考以后发现dict内部存放的顺序和key放入的顺序没有关系,因为它是采用哈希表的原理.

正确思路是只用一个dict,键为s的字母,值为t相同位置的字母,如果s中的字母已经在dict中了,则判断对应的键是否与此时t中的字母相等,如果不相等则false.如果s中的字母不在dict中,判断此时t中的字母是否在dict中有值相等,如果有则返回false,否则将该键值对存入dict.

class Solution:
    def isIsomorphic(self, s, t):
        """
        :type s: str
        :type t: str
        :rtype: bool
        """
        if len(s) != len(t):
            return False
        hashmap = {}
        for i in range(len(s)):
            if s[i] in hashmap:
                if hashmap[s[i]] != t[i]:
                    return False
            else:
                if t[i] in hashmap.values():
                    return False
                else:
                    hashmap[s[i]] = t[i]
        return True

 

---274.H-Index

给定一个非负数组,代表一位科学家的引用因子,求出这位科学家的H-Index.H-index是指他至多有h篇论文分别被引用了至少h次.

计算H-index的方法是将引用因子降序排好,然后找到第一个比引用因子大的序号,将序号-1就是H-index.

class Solution:
    def hIndex(self, citations):
        """
        :type citations: List[int]
        :rtype: int
        """
        if citations == []:
            return 0
        citations.sort(reverse=True)
        for i in range(len(citations)):
            if i + 1 > citations[i]:
                return i

        return len(citations)

 

---299.Bulls and Cows

一个猜数字的游戏,给定目标数secret和猜测数guess,猜测数中和目标数大小相同且位置相同的叫bulls,大小相同但位置不同的叫cows,要求给出bulls和cows的数量.

首先用map将secret和guess变为数字list,另外定义两个长度为10的list,然后同时遍历这两个list,如果数字相同则bulls+1,否则在对应的list的对应位置+1.遍历结束后比较list每个位置的较小者,相加就得到cows的数量.

class Solution:
    def getHint(self, secret, guess):
        """
        :type secret: str
        :type guess: str
        :rtype: str
        """
        nums1 = list(map(int, secret))
        nums2 = list(map(int, guess))
        bulls = 0
        cows = 0
        l1 = [0]*10
        l2 = [0]*10

        for i in range(len(nums1)):
            if nums1[i] == nums2[i]:
                bulls += 1
            else:
                l1[nums1[i]] += 1
                l2[nums2[i]] += 1

        for i in range(10):
            cows += min(l1[i], l2[i])
            
        return str(bulls)+'A'+str(cows)+'B'

 

 Depth-first Search

---117.Populating Next Right Pointers in Each Node ||

给定一棵二叉树,将每个结点的next结点设为它右边的相邻结点,如果不存在这样的结点则设为NULL.

首先建立一个tali结点和一个head结点,其中head结点用于保存tail结点最初的位置.然后遍历当前root,首先将tail.next指向root.left,如果存在则将tail移动至tail.next,然后将tail.next指向root.right,如果存在则将tail移动至tali.next.遍历完以后将root指向root.next(因为root比tail高一层,所以root层的next结构已经固定了).如果root存在则重复上述过程,否则将tail指向一开始的head结点,将root指向head的next,即将root下移了一层.

# Definition for binary tree with next pointer.
# class TreeLinkNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
#         self.next = None

class Solution:
    # @param root, a tree link node
    # @return nothing
    def connect(self, root):
        tail = head = TreeLinkNode(0)
        while root:
            tail.next = root.left
            if tail.next:
                tail = tail.next
            tail.next = root.right
            if tail.next:
                tail = tail.next
            root = root.next
            if not root:
                tail = head
                root = head.next

 

---200.Number of Islands

给定一个二维网格,其中'1'代表陆地,'0'代表水.岛是指一块被水包围的竖直方向和水平方向相连的陆地.假设网格的四周都是水,求其中岛的数量.

经典的DFS思想,遍历网格,如果当前位置是1就调用dfs函数.在dfs中首先进行边界判断,然后如果当前位置是'1'则改为'#',之后对位置的前后左右位置调用dfs函数.

class Solution:
    def numIslands(self, grid):
        """
        :type grid: List[List[str]]
        :rtype: int
        """
        if not grid:
            return 0

        count = 0
        for i in range(len(grid)):
            for j in range(len(grid[0])):
                if grid[i][j] == '1':
                    self.dfs(grid, i, j)
                    count += 1
        return count

    def dfs(self, grid, i, j):
        if i<0 or j<0 or i>=len(grid) or j>=len(grid[0]) or grid[i][j] != '1':
            return
        grid[i][j] = '#'
        self.dfs(grid, i+1, j)
        self.dfs(grid, i-1, j)
        self.dfs(grid, i, j+1)
        self.dfs(grid, i, j-1)

 

---98.Validate Binary Search Tree

给定一棵二叉树,判断它是不是一棵二叉查找树(左子树的所有结点都比该结点小,右子树的所有结点都比该结点大,且左右子树都是二叉查找树).

 

 

尚未分类

---1.Two Sum

在列表中找到两个数,使得它们的和等于某一给定值,返回这两个数的位置.时间复杂度:O(n),python中的字典其实就是哈希表的应用,所以我们通过字典用哈希表来降低查找的时间复杂度

class Solution:
    def twoSum(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: List[int]
        """
        d = {}
        for i, n in enumerate(nums):
            m = target - n
            if m in d:
                return [d[m], i]
            else:
                d[n] = i

 

---2.Add Two Numbers

将两个倒序存放在单链表里的数相加,将结果倒序存储在单链表里返回.思路非常简单,先将两个单链表中的数字分别提取出来求和,然后将=求得的和存入一个单链表,实际上相加这一步也可以直接在原链表中完成,只需要添加判断条件while(l1 or l2 or carry)即可.

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def addTwoNumbers(self, l1, l2):
        """
        :type l1: ListNode
        :type l2: ListNode
        :rtype: ListNode
        """
        node1 = l1
        node2 = l2
        l3 = ListNode(0)
        l3.next = ListNode(0)#[0],[0]的特殊情况
        node3 = l3
        
        sum1 = 0
        coe = 1
        while not node1 is None:
            sum1 += node1.val * coe
            coe *= 10
            node1 = node1.next
        
        sum2 = 0
        coe =1
        while not node2 is None:
            sum2 += node2.val * coe
            coe *= 10
            node2 = node2.next
        
        sum = sum1 + sum2
        
        while sum > 0:
            node3.next = ListNode(sum % 10)
            node3 = node3.next
            sum //= 10
            
        return l3.next    

 

---3.Longest Substring Without Repeating Characters

找到字符串中没有重复字符的最大子串.一开始没有想到用字典,而是直接用str来存储字串,时间复杂度是O(n^2),后来用字典将时间复杂度降到了O(n).注意到仅当字典中出现重复值且该重复值在strat区段里时才移动start.另外用了Sliding Window的思想,每次将strat移动到重复值的下一位置.

class Solution:
    def lengthOfLongestSubstring(self, s):
        """
        :type s: str
        :rtype: int
        """
        start = 0
        max_length = 0
        substring = {}
        for i, c in enumerate(s):
            if c in substring and start <= substring[c]:#只有当重复值是在start后面出现时才移动start
                start = substring[c] + 1#Slding Window的思想
            else:
                max_length = max(max_length, i - start + 1)
            substring[c] = i
            
        return max_length

 

---5.Longest Palindromic Substring

最长回文子串问题,一开始我的思路如下:回文子串的特点是首尾字母相同,所以我对每一个字母都找到位于它后面的相同字母,利用切片判断这一段是否为回文子串(str[i:j]==str[i:j][::-1]).虽然AC了但是时间复杂度很高,主要是因为str.find操作非常耗时.

后来看了Solution发现这是一道可以用动态规划解决的问题,思路是若s是回文字串,令s'=s加上s左右两侧的两个字母,如果这两个字母相同则s'也是回文字串.重写代码如下:

class Solution:
    def longestPalindrome(self, s):
        """
        :type s: str
        :rtype: str
        """
        max = 0
        palindromic = '' if len(s) == 0 else s[0]
        for i in range(len(s)):
            length = 1
            while i - length >=0 and i + length < len(s) and s[i-length] == s[i+length]:
                tmp = s[i-length:i+length+1]
                if len(tmp) > max:
                    max = len(tmp)
                    palindromic = tmp
                length += 1
            length = 1
            while i - length + 1  >=0 and i + length < len(s) and s[i-length+1] == s[i+length]:
                tmp = s[i-length+1:i+length+1]
                if len(tmp) > max:
                    max = len(tmp)
                    palindromic = tmp
                length += 1
        return palindromic

这道题还有经典的Manacher算法,可以看这篇文章.Discuss里的算法实现在这里.

另外在Discuss里发现了另一种做法,思路是一段回文字符串的后面新增了一个字母,如果新字符串仍是回文字符串的话只有两种可能:形如bb+b,也就是多了一个字母,或形如a(bb)+a,算上原回文字符串的前一个字母共多了两个字母.基于这个思路可以写出代码.因为用到了切片,在题例上运行的速度甚至比Manacher算法还快.

 

---6.ZigZag Conversion

一道将字符串做之字形排列的题目.我们用n表示行数,将排列后得到的字符串分为完整竖列和折线两部分.每个完整竖列有n个数,每两个完整竖列之间的折线有n-2列,每列一个数,因此每两个完整竖列中同一行的数的间隔是n+n-2=2n-2.同时我们发现,除了第一行和最后一行之外的第i行都有折线,第i行的第一个折线是第2n-i个数.于是可以遍历输出每一行,判定条件是这一行我们要输出的数字是否超出了字符串的长度.

class Solution:
    def convert(self, s, numRows):
        """
        :type s: str
        :type numRows: int
        :rtype: str
        """
        zigzag = ''
        
        if numRows == 1 or numRows == 0 or numRows >= len(s):
            return s

        
        
        space = 2 * numRows - 2
        for i in range(1,numRows+1):
            n = 0
            if i == 1 or i == numRows:
                while i + n * space <= len(s):
                    zigzag += s[i+n*space-1]
                    n += 1
            else:
                while i + n * space <= len(s):
                    zigzag += s[i+n*space-1]
                    if (2 * numRows - i) + (n * space) <= len(s):
                        zigzag += s[(2*numRows-i)+(n*space)-1]
                    n += 1
        
        return zigzag

ZigZag Conversion

 

---7.Reverse Integer

将给定的数字倒序输出.非常简单的一道题

class Solution(object):
    def reverse(self, x):
        """
        :type x: int
        :rtype: int
        """
        tmp = abs(x)
        
        sum = 0
        while tmp > 0:
            sum = sum * 10 + tmp % 10
            tmp = tmp // 10

        sum = sum if x >= 0 else -sum

        return sum if sum < 2**31 and sum > -2**31 else 0
 

 

---8.String to Integer(atoi)

将给定字符串中符合条件的一串数字字符转化为int类型返回.我的思路是设定标志位start=0和符号位sign,遍历字符串,当start=0时遇到空格则continue,遇到+则记录sign=1,遇到-则记录sign=-1,遇到数字则记录数字;当strat=1时代表已经找到了第一个数字或符号位,此时遇到除数字之外的字符都break,遇到数字则继续记录数字.注意我们得到的整数值不能超过INT_MAX和INT_MIN.后来发现其实用str.strip()函数来去除字符串头尾的空格会更方便.

class Solution(object):
    def myAtoi(self, str):
        """
        :type str: str
        :rtype: int
        """
        ans = 0
        start = 0
        sign = 0
        if str.isspace() is True:
            print(0)
        for i in str:
            if start == 0:
                if i.isspace() is True:
                    continue
                if i == '+':
                    sign = 1
                elif i == '-':
                    sign = -1
                elif i.isdigit() is True:
                    sign = 1
                    ans = ans * 10 + int(i)
                else:
                    break
                start = 1
            else:
                if i.isdigit() is True:
                    ans = ans * 10 + int(i)
                else:
                    break

        ans = sign * ans
        if ans >= 2147483647:
            return 2147483647
        elif ans <= -2147483648:
            return -2147483648
        else:
            return ans

 

---9.Palindrome Number

判断一个数字是否是回文数.题目要求不能用额外的空间,否则可以利用python的字符串切片轻松解决.我的思路是求出该整数的位数,判断第一位数和最后一位数是否相同,如果相同则将位数/100,然后将原数字的首尾两个数删除,最后如果位数<1说明是回文数.

class Solution(object):
    def isPalindrome(self, x):
        """
        :type x: int
        :rtype: bool
        """
        if x < 0:
            return False
        
        high = 1
        while x / high >= 10:
            high *= 10

        while x // high == x % 10:
            x = x % high // 10
            high /= 100
            if high < 1:
                return True
            
        return False

 

---12.Integer to Roman

将十进制数字转化为罗马数字.比较简单的一道题.我的思路是判断当前位数,改变代表1/5/10的字符然后逐位输出.也可以直接将每位上的各种字符表示存在列表里,然后直接取出.

class Solution(object):
    def intToRoman(self, num):
        """
        :type num: int
        :rtype: str
        """
        carry = 1
        roman = ''

        while num != 0:
            n = num % 10
            num //= 10
            if carry == 1:
                numeral_1 = 'I'
                numeral_5 = 'V'
                numeral_10 = 'X'
            elif carry == 10:
                numeral_1 = 'X'
                numeral_5 = 'L'
                numeral_10 = 'C'
            elif carry == 100:
                numeral_1 = 'C'
                numeral_5 = 'D'
                numeral_10 = 'M'
            else:
                numeral_1 = 'M'
                numeral_5 = ''
                numeral_10 = ''

            if 1 <= n <= 3:
                roman = numeral_1 * n + roman
            elif n == 4:
                roman = numeral_1 + numeral_5 + roman
            elif 5 <= n <= 8:
                roman = numeral_5 + numeral_1 * (n - 5) + roman
            elif n == 9:
                roman = numeral_1 + numeral_10 + roman

            carry *= 10

        return roman

 

---13.Roman to Integer

将罗马数字转化为十进制数字.非常无聊的一道题.比较简单的方法是写非常多的if语句来判断,或者将罗马数字与对应的十进制数字存入字典来转换.下面是我在discuss里看到的一个方案,巧妙利用了罗马数字"大数前面的小数用来减,大数后面的小数用来加"这个特点.

class Solution(object):
    def romanToInt(self, s):
        """
        :type s: str
        :rtype: int
        """
        roman_map = {
            "I": 1,
            "V": 5,
            "X": 10,
            "L": 50,
            "C": 100,
            "D": 500,
            "M": 1000,
        }
        result = 0
        last_num = None
        for char in s:
            current_num = roman_map[char]
            if last_num is None or last_num >= current_num:
                result += current_num
            elif last_num < current_num:
                result += current_num - 2 * last_num
            last_num = current_num
        return result
            

 

---14.Longest Common Prefix

找最长公共前缀字符串.我的思路是找出列表中最短的字符串,然后对最短字符串的每个字符都在列表中遍历,直到出现不同或者遍历结束为止.在discuss里看到很多方法利用了python中的sort(),min(),max()这些内置方法对字符串排序,会使时间快很多.

class Solution(object):
    def longestCommonPrefix(self, strs):
        """
        :type strs: List[str]
        :rtype: str
        """
        prefix = ''
        
        if strs == []:
            return prefix
    
        minimum = float("inf")
        for s in strs:
            minimum = min(len(s), minimum)
            
        i = 0
        for j in range(minimum):
            for i in range(len(strs)):
                while strs[i][j] != strs[0][j]:
                    return prefix
            prefix = prefix + strs[0][j]
        
        return prefix

 

---15.3Sum

给定一个数组,找到其中三个数的和为零的所有可能,以列表形式返回.这道题的基本思路是先将数组排序,从左往右遍历一次.在遍历每个数的过程中设立两个指针,如果三个数的和大于零则左移右指针,如果三个数的和小于零则右移左指针,直到两个指针相遇.注意我们用的是set()来存储找到的结果,可以避免list中出现重复.在此基础上,我增加了一个对排序过的数组的操作,即当最左边两个数与最右边一个数的和大于零时删去最右边的数,当最左边一个数与最右边两个数的和小于零时删去最左边的数.这个操作大大提升了运行速度.

class Solution(object):
    def threeSum(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        zeros = set()
        nums.sort()
        if len(nums) < 3:
            return []

        if nums.count(0) > len(nums)-2:
            return [[0, 0, 0]]
        
        while len(nums) > 3 and (nums[0]+nums[1]+nums[-1] > 0 or nums[-1]+nums[-2]+nums[0] < 0):
            if nums[0] + nums[1] + nums[-1] > 0:
                nums.remove(nums[-1])
            else:
                nums.remove(nums[0])
        
        for i in range(len(nums)-2):
            if nums[i] > 0:
                break
            j = i + 1
            k = len(nums) - 1
            while j < k:
                sum = nums[i] + nums[j] + nums[k]
                if sum == 0:
                    zeros.add((nums[i], nums[j], nums[k]))
                    j += 1
                    continue
                elif sum < 0:
                    j += 1
                else:
                    k -= 1

        return list(map(list,zeros))