Atcoder 补题记录
AGC047
A Integer Product
题意:问有多少个二元组 \((a_i,a_j) \ (i<j)\),满足 \(a_i \times a_j\) 是一个整数,保证 \(a_i\) 是一个小数位不超过九位的实数。
做的时候感觉先乘个 \(10^9\) 再说,于是问题转化为有多少个二元组 \((a_i,a_j)\) ,满足 \(a_i \times a_j \equiv 0 (\mod 10^{18})\)
对 \(10^{18}\) 分解质因数为 \(2^{18} \times 5^{18}\),问题转化为有多少二元组,它们的 \(2\) 的指标之和与 \(5\) 的指标之和均大于或等于 \(18\)
用桶就可以维护了
B First Second
题意简述:自己去看原题面 https://atcoder.jp/contests/agc047/tasks/agc047_b
根据题意可以发现,如果 \(A\) 经过操作可以变成 \(B\) 的话,那么 \(B\) 去掉第一个字母后的字符串 \(B'\) 必定是 \(A\) 的后缀,而 \(A\) 去掉后缀 \(B'\) 后的字符串 \(A'\) 中则必定包含 \(B\) 的第一个字母。
然后就可以用 trie 维护了,每个节点的信息 \(t_i\) 表示包含该前缀的所有字符串中,去掉前缀后包含字母 \(i\) 的字符串有多少个。
然后就可以轻松做了。但是题意是问有多少二元组 \((A_i,A_j)\) 满足 \(A_i\) 可以变化到 \(A_j\) 或 \(A_j\) 可以变化到 \(A_i\)
于是可以全局做一遍然后查询每一个字符串。
代码如下:
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
int tot;
struct trie{
int ch[26],t[26];
}tr[N<<2];
int cnt[26];
void extend(string id){
for(int i=0;i<='z'-'a';++i) cnt[i]=0;
int n=id.size();
for(int i=0;i<n;++i) cnt[id[i]-'a']++;
int p=0;
for(int i=0;i<n;++i){
for(int j=0;j<='z'-'a';++j)
tr[p].t[j]+=(cnt[j]>0);
if(!tr[p].ch[id[i]-'a']) tr[p].ch[id[i]-'a']=++tot;
p=tr[p].ch[id[i]-'a'];
cnt[id[i]-'a']--;
}
}
int query(string id){
int n=id.size(),p=0;
if(n==1) return tr[0].t[id[0]-'a'];
for(int i=0;i<n-1;++i){
if(!tr[p].ch[id[i]-'a']) return 0;
p=tr[p].ch[id[i]-'a'];
//cout<<p<<" "<<id[i]-'a'<<endl;
}
return tr[p].t[id[n-1]-'a'];
}
void Reverse(string &s){
int i=0,j=s.size()-1;
while(i<j) swap(s[i],s[j]),++i,--j;
}
string id[N];
int main(){
int n,len;
cin>>n;long long ans=0;
for(int i=1;i<=n;++i){
cin>>id[i];
Reverse(id[i]);
extend(id[i]);
}
for(int i=1;i<=n;++i)
ans+=query(id[i]);
cout<<ans-n;
return 0;
}
C Product Modulo
题意简述:求 \(\sum_{i=1}^n \sum_{j=i+1}^n a_i \times a_j \mod P,n \leq 2 \times 10^5,P=200003\)
发现 \(P=200003\) 是个质数,原根 \(G=2\)
先想到可以枚举余数然后计算它出现的次数,设这个次数为 \(C_i\),表示 \(i\) 出现了 \(C_i\) 次。
那么计算的时候就是
\(C_k=\sum_{i \times j=k} f_i \times f_j\)
其中 \(f_i\) 表示 \(i\) 在 \(a\) 数组中出现的次数。
上面这个东西是个老经典题,可以用原根来转化。详情请见 [SDOI2015] 序列统计
D Twin Binary Trees
我不会的题
题意简述:。。。自己去看原题
考虑这个环出现的四个关键点,其中两个关键点 \(i,j\) 出现在第一颗子树的叶子节点,而另外两个关键点 \(p_i,p_j\) 则如题意所属。
那么可以考虑枚举 \(i,j\) 的 \(LCA\),用一个类似于分治的做法去实现这个过程。
对于左边的每个点 \(i\),可以对它的 \(p_i\) 的所有祖先计算贡献
对于右边的每个点 \(j\),可以对它的 \(p_i\) 的所有祖先统计贡献
具体看代码,个人觉得还是很好懂的
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int mod=1e9+7,N=1<<20;
int cnt[N],a[N],p[N],n,ans;
void solve(int u,int l,int r){
if(l==r) return (void)(a[l]=u);
int mid=(l+r)>>1;
solve(u<<1,l,mid);
solve(u<<1|1,mid+1,r);
for(int i=l;i<=mid;++i)
a[i]=a[i]*u%mod;
for(int i=l;i<=mid;++i){
int v=(1<<n-1)+p[i]-1,num=a[i];
while(v) num=num*v%mod,cnt[v]=(cnt[v]+num)%mod,v>>=1;
}
for(int i=mid+1;i<=r;++i){
int v=(1<<n-1)+p[i]-1,num=a[i],las=0;
while(v) las=las*v%mod,ans=(ans+(cnt[v]-las+mod)%mod*num%mod)%mod,num=num*v%mod,las=cnt[v],v>>=1;
}
for(int i=l;i<=mid;++i){
int v=(1<<n-1)+p[i]-1;
while(v) cnt[v]=0,v>>=1;
}
for(int i=mid+1;i<=r;++i)
a[i]=a[i]*u%mod;
}
signed main(){
cin>>n;
for(int i=1;i<=(1<<n-1);++i)
cin>>p[i];
solve(1,1,1<<n-1);
cout<<ans;
return 0;
}
E Product Simulation
卧槽好难
题意简述:同上
可以考虑用 \(2\) 的幂次方来进行构造,最后只要统计 \(\sum_{i=0}^{bit}\sum_{j=0}^{bit} [(A>>i)\&1] \times [(B>>i)\&1] \times 2^{i+j}\) 即可。
对于 \(2^k\) 的构造:
可以构造出 \(A<(A+B) \times 2\) 或者 \(B< (A+B) \times 2\),来构造出 \(1\),随后就可以通过 \(a_{k2}=a_{k1}+a_{k1}\) 来构造出 \(2\) 的幂次。
对于 \([(A>>i)\&1]\) 的构造:
有一个简单的构造,就是从低到高枚举位数 \(i\) ,统计 \([a_{sum}+2^{i} \leq A]\) 是否为真,如果是真那么 \([(A>>i)\&1]=1,a_{sum}+=2^{i}\)
\([(A>>i)\&1]=1\) 也就是 \([a_{sum}+2^{i} < A+1]\)
\(a_{sum}+=2^{i}\) 也就是 \(a_{sum}+=2^i \times [a_{sum}+2^{i} < A+1]\)
把这些都构造出来的话,那么做起来就很轻松了。
代码如下:
#include<bits/stdc++.h>
using namespace std;
struct Opt{
int opt,x,y,z;
Opt(){}
Opt(int _o,int _x,int _y,int _z){
opt=_o;x=_x;y=_y;z=_z;
}
}a[200005];int tot;
int pw[205],bit[205][2],cnt;
void Pw(){
a[++tot]=Opt(1,0,3,3);
a[++tot]=Opt(1,1,3,3);
a[++tot]=Opt(1,3,3,3);
a[++tot]=Opt(0,1,3,3);
cnt=3;pw[0]=3;
for(int i=1;i<32;++i)
pw[i]=++cnt,a[++tot]=Opt(1,pw[i-1],pw[i-1],pw[i]);
}
void apart(int type){//type= A or B?
a[++tot]=Opt(1,type,pw[0],type);
int sum=++cnt;
for(int i=31;i>=0;--i){
int res=++cnt;
a[++tot]=Opt(1,sum,pw[i],res);// res = sum + 2^i
a[++tot]=Opt(0,res,type,res); // res < type ?
bit[i][type]=res; // (type>>i)&1
++cnt; a[++tot]=Opt(1,res,cnt,cnt);
for(int j=1;j<=i;++j) a[++tot]=Opt(1,cnt,cnt,cnt);
a[++tot]=Opt(1,sum,cnt,sum);
}
}
int main(){
//freopen("1.out","w",stdout);
Pw();apart(0),apart(1);
for(int i=0;i<32;++i)
for(int j=0;j<32;++j){
int res=++cnt;
a[++tot]=Opt(1,bit[i][0],bit[j][1],res);
a[++tot]=Opt(0,pw[0],res,res);
for(int k=1;k<=i+j;++k)
a[++tot]=Opt(1,res,res,res);
a[++tot]=Opt(1,res,2,2);
}
cout<<tot<<endl;
for(int i=1;i<=tot;++i)
cout<<((a[i].opt==1)?"+":"<")<<" "<<a[i].x<<" "<<a[i].y<<" "<<a[i].z<<endl;
return 0;
}
F Rooks
可 做 题
有一个暴力的想法是朴素 dp,先把点按 x 排序,之后 \(f_{l,r,0/1}\) 表示从 \(l \sim r\) 的点全被吃掉,而王在最左边/最右边的点上时的最小步数,转移显然。
发现复杂度很不优美,所以可以考虑把一些单调的点缩成一个矩阵,于是就可以把原棋盘通过这种方式划分成一个个矩阵,然后在这个矩阵上进行 dp
考虑单调的一系列点所走过的距离,实际上就是第一个点与最后一个点的曼哈顿距离减去点的总数。
贡献会算了之后可以直接跑记搜,至于复杂度为什么是对的我也不知道
代码如下:
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define fi first
#define se second
const int N=2e5+5;
const long long inf=1e18;
pair< pair<int,int> , int > a[N];
int n,x[N],y[N],l[N],r[N];
map<int,long long> f[2][N];
long long dis(pair<int,int> i,pair<int,int> j){
return abs(x[i.fi]-x[j.fi])+abs(y[i.se]-y[j.se]);
}
long long dfs(int mn,int mx,int l,int r,int k){
if(f[k][l].count(r)) return f[k][l][r];
int L=::l[l-1],R=::r[r+1];long long ans=inf;
if(l>1 && (a[l-1].fi.se==mn-1 || a[l-1].fi.se==mx+1))
ans=min(ans,dfs(min(a[L].fi.se,mn),max(a[L].fi.se,mx),L,r,0)+dis(a[L].fi,k==0?a[l].fi:a[r].fi));
if(r<n && (a[r+1].fi.se==mn-1 || a[r+1].fi.se==mx+1))
ans=min(ans,dfs(min(a[R].fi.se,mn),max(a[R].fi.se,mx),l,R,1)+dis(a[R].fi,k==0?a[l].fi:a[r].fi));
f[k][l][r]=(ans==inf?l-r:ans);
return f[k][l][r];
}
long long ans[N];
signed main(){
cin>>n;
for(int i=1;i<=n;++i)
cin>>x[i]>>y[i],a[i]=make_pair(make_pair(x[i],y[i]),i);
sort(a+1,a+n+1);
sort(x+1,x+n+1);
sort(y+1,y+n+1);
for(int i=1;i<=n;++i)
a[i].fi.fi=lower_bound(x+1,x+n+1,a[i].fi.fi)-x,
a[i].fi.se=lower_bound(y+1,y+n+1,a[i].fi.se)-y;
l[1]=1;
for(int i=2;i<=n;++i)
if(abs(a[i-1].fi.se-a[i].fi.se)==1) l[i]=l[i-1];
else l[i]=i;
r[n]=n;
for(int i=n-1;i>=1;--i)
if(abs(a[i+1].fi.se-a[i].fi.se)==1) r[i]=r[i+1];
else r[i]=i;
//for(int i=1;i<=n;++i)cout<<a[i].fi.fi<<" "<<a[i].fi.se<<endl;
for(int i=1;i<=n;++i)
ans[a[i].se]=dfs(a[i].fi.se,a[i].fi.se,i,i,0);
for(int i=1;i<=n;++i)
cout<<ans[i]<<endl;
return 0;
}
AGC046
这是一场非常牛逼的 dp 赛
It was a great DP contest ——外国网友
A - Takahashikun, The Strider
结论题,有结论 \(K=\frac{360}{\gcd(360,X)}\)
B - Extension
可以 dp,设 \(f_{i,j}\) 为从 \((A,B)\) 扩展染色到 \((i,j)\) 的方案数
如果把 dp 方程设为 \(f_{i,j}=f_{i-1,j}\times j+f_{i,j-1} \times i\) 的话,显然会算重。
发现算重的方案均由 \((i-1,j-1)\) 扩展 \(1\) 行 \(1\) 列而成的,并且在边角染色的方案不会算重,于是有 \(f_{i,j}=f_{i-1,j} \times j +f_{i,j-1} \times i-f_{i-1,j-1} \times (i-1) \times (j-1)\)
C - Shift
把 \(0\) 作为分界点,把分界点之间的 \(1\) 的数量设为 \(cnt_i\),发现方案的不同之处仅在于 \(cnt_i\) 往左边搬运 \(1\) 的个数或者 \(cnt_i\) 往右边得到 \(1\) 的个数。
那么可以设置状态 \(f_{i,j,k}\) 为目前在前 \(i\) 组 \(1\) 当中,通过搬运已经获取了 \(j\) 个 \(1\),且搬运次数为 \(k\) 的方案数。
注意判断一下当前 \(dp\) 状态是否合法。另附代码如下。
#include<bits/stdc++.h>
using namespace std;
const int mod=998244353;
void add(int &x,int y){
x=(x+y)%mod;
}
int n,k,f[305][305][305],cnt[505],suf[505];
char s[505];
signed main(){
scanf("%s%d",(s+1),&k);
n=strlen(s+1);k=min(n,k);
int res=0,tot=0;
//cout<<n<<" "<<k<<endl;
for(int i=1;i<=n;++i)
if(s[i]=='0') cnt[++tot]=res,res=0;
else ++res;
if(res) cnt[++tot]=res;
for(int i=tot;i>=1;--i)
suf[i]=suf[i+1]+cnt[i];
f[0][0][0]=1;
for(int i=1;i<=tot;++i)
for(int one=0;one<=n;++one)
for(int st=0;st<=k;++st)
if(f[i-1][one][st]){
for(int v=0;v<=cnt[i];++v){
int tmp=one-(cnt[i]-v);
if(tmp>=0 && tmp<=suf[i+1]){;
add(f[i][tmp][st],f[i-1][one][st]);
}
}
for(int v=cnt[i]+1;one-(cnt[i]-v)<=suf[i+1];++v){
int tmp=one-(cnt[i]-v);
if(tmp>=0 && tmp<=suf[i+1]){
add(f[i][tmp][st+v-cnt[i]],f[i-1][one][st]);
}
}
}
int ans=0;
for(int st=0;st<=k;++st)
add(ans,f[tot][0][st]);
cout<<ans;
return 0;
}
D - Secret Passage
可以枚举一下分割线,然后求出把分割线前的字符插入分割线后的字符能得到的方案数。
设 \(f_{i,j,k}\) 为把原串 \(s_{1 \dots i}\) 中的 \(j\) 个 \(0\) 字符, \(k\) 个 \(1\) 字符插入到 \(s_{i+1 \dots n}\) 的方案数。
发现这样很容易算重,这里给出一个不会算重的方案:对于 \(s_i=0\) 的情况,只往它的后面插入若干个 \(1\),反之则插入若干个 \(0\)
但是这样还不够,因为我们并不知道原串 \(s_{1 \dots i}\) 按照题目中的方式是否能挑出 \(j\) 个 \(0\) 和 \(k\) 个 \(1\)
对于这个可以再 dp 一下,具体可以看代码,还是比较好懂的
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int mod=998244353;
int f[305][305][305];bool flag[305][305][305];
void add(int &x,int y){
x=(x+y)%mod;
}
char s[305];
signed main(){
cin>>(s+1);
int n=strlen(s+1);
f[n][0][0]=1;
for(int i=n;i>=1;--i)
for(int j=0;j<=i;++j)
for(int k=0;j+k<=i;++k)
if(f[i][j][k]){
add(f[i-1][j][k],f[i][j][k]);
if(s[i]=='0') add(f[i][j][k+1],f[i][j][k]);
else add(f[i][j+1][k],f[i][j][k]);
}
for(int i=0;i<n;++i){
flag[i][0][0]=1;
for(int j=0;j<=i;++j)
for(int k=0;j+k<=i;++k)
if(flag[i][j][k]){
flag[i+1][j][k]=1;
if(s[i+1]=='0' || s[i+2]=='0') flag[i+2][j+1][k]=1;
if(s[i+1]=='1' || s[i+2]=='1') flag[i+2][j][k+1]=1;
if(s[i+1]=='0' && k) flag[i+1][j+1][k-1]=1;
if(s[i+1]=='1' && j) flag[i+1][j-1][k+1]=1;
}
}
flag[n][0][0]=0;
int ans=0;
for(int i=0;i<=n;++i)
for(int j=0;j<=i;++j)
for(int k=0;j+k<=i;++k)
if(flag[i][j][k]) add(ans,f[i][j][k]);
cout<<ans;
return 0;
}
E - Permutation Cover
不会讲,去看 Froggy 的题解
F - Forbidden Tournament
也不会讲,去看 AutumnKite 的题解
AGC045 题解
A - Xor Battle
方便起见,设玩家 \(0\) 的 \(a_i\) 为 \(a_{i,0}\),设玩家 \(1\) 的 \(a_i\) 为 \(a_{i,1}\)
从前往后考虑,设当前的异或和为 \(x\) ,当前的回合为玩家 \(1\) 的回合,考虑什么样的情况下对于玩家 \(0\) 是无解的。
-
\(a_{i,1} =x\),那么需要满足后面没有 \(a_{i,0}\) 的子集的异或和为 \(a_{i,1}\)
-
\(a_{i,1} \not = x\),正着考虑比较难,那么反着考虑,什么样的情况下对于玩家 \(1\) 是无解的。如果后面有 \(a_{i,0}\) 的子集的异或和为 \(x\) 且有 \(a_{i,0}\) 的子集的异或和为 \(a_{i,1} \oplus x\),那么对于玩家 \(1\) 是无解的。
发现如果有 \(a_{i,0}\) 的子集的异或和为 \(x\) 且有 \(a_{i,0}\) 的子集的异或和为 \(a_{i,1} \oplus x\),那么必然有一个 \(a_{i,0}\) 的子集的异或和为 \(x\)。于是条件再度转化为,需要满足后面没有 \(a_{i,0}\) 的子集的异或和为 \(a_{i,1}\)
于是问题变成对于每个 \(a_{i,1}\),后面是否有 \(a_{i,0}\) 的子集的异或和为 \(a_{i,1}\)。这个可以用线性基来维护。
代码如下:
#include<bits/stdc++.h>
using namespace std;
#define int long long
int base[65],a[205];char s[205];
bool insert(int x){
for(int i=64;i>=0;--i)
if((x>>i)&1){
if(!base[i]) return base[i]=x,1;
x^=base[i];
}
return 0;
}
bool solve(int n){
memset(base,0,sizeof(base));
for(int i=1;i<=n;++i)
cin>>a[i];
cin>>(s+1);
for(int i=n;i>=1;--i)
if(insert(a[i]) && s[i]=='1') return 1;
return 0;
}
signed main(){
int T,n;
cin>>T;
while(T--){
cin>>n;
cout<<solve(n)<<endl;
}
return 0;
}
B - 01 Unbalanced
把 \(0\) 看做 \(-1\),把 \(1\) 看做 \(1\),设 \(sum_i=\sum_{j=1}^n s_j\),那么本题的目标就转化成在问号里填数并使 \(\max\limits_{j<i}\{|sum_{i}-sum_{j}|\}\) 最小。
发现 \(\max\limits_{j<i}\{|sum_i-sum_j| \}=\max\{sum_i\}-\min\{sum_i\}\)
我们可以枚举 \(\max\{sum_i\}\) 的值,设这个值为 \(M\),然后求 \(f(M)=\max\limits_{\max\{sum_i\} \leq M}\{\min\{sum_i\}\}\)
那么答案也就是 \(\min\limits_{M}\{M-f(M)\}\)
考虑这个值的下界,当所有问号里填的数字均为 \(0\) 时,\(\max\{sum_i\}\) 的值最小,设此时 \(\max\{sum_i\}\) 的值为 \(Z\),也就是 \(M\) 的下界。
考虑如何求出 \(f(M)\),可以从前往后进行贪心,如果问号的位置填上 \(1\) 后不会有 \(sum_i\) 的值大于 \(M\),那么就将问号填上 \(1\)。这样就使 \(\min\{sum_i\}\) 最大,也就求出了 \(f(M)\)
发现 \(f(M)+2 \geq f(M+2)\),即 \(M-f(M) \leq M+2-f(M+2)\),那么实际上只需要求出 \(f(Z)\) 与 \(f(Z+1)\) 即可。
代码如下:
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
char s[N];
int sum[N],mx[N],n;
int f(int M){
for(int i=1,cnt=0;i<=n;++i){
if(s[i]=='?'){
if((cnt+1)*2+mx[i]<=M) ++cnt,sum[i]=1;
else sum[i]=-1;
}
else sum[i]=(s[i]=='0'?-1:1);
sum[i]+=sum[i-1];
}
return *min_element(sum,sum+n+1);
}
int main(){
cin>>(s+1);n=strlen(s+1);
for(int i=1;i<=n;++i){
if(s[i]=='?') sum[i]=-1;
if(s[i]=='1') sum[i]=1;
if(s[i]=='0') sum[i]=-1;
sum[i]+=sum[i-1];
}
for(int i=n;i>=0;--i)
if(i+1<=n)mx[i]=max(sum[i],mx[i+1]);
else mx[i]=sum[i];
//for(int i=0;i<=n;++i)cout<<mx[i]<<" ";cout<<endl;
int Z=mx[0];
cout<<min(Z-f(Z),Z+1-f(Z+1));
return 0;
}
C - Range Set
先考虑 \(A<B\) 时的情况。
把操作转化为,可以把连续 \(A\) 个 \(0\) 字符转化为 \(1\) 字符,可以把连续 \(B\) 个 \(1\) 字符转化为 \(0\) 字符,那么问题也转化成,有多少个串 \(S\) 可以经由这样的操作变为给定串(即仅由字符 0 构成的串)
先考虑字符串 \(S\) 内包含由 \(1\) 构成的大小为 \(B\) 的子串的情况。如果子串的左侧是 1 的话,则将其加入子串,否则,则可以将子串全部转为 0,再将左侧加入子串,再将子串全部转为 1。右侧同理,所以最终子串能扩展到长度为 \(|S|\),也就是给定串。
如果没有大小为 \(B\) 的子串的情况,则可以通过 “把连续 \(A\) 个 \(0\) 字符转化为 \(1\) 字符” 这样的操作来使子串大小为 \(B\)。如果无法通过这样的操作,那么这个字符串 \(S\) 显然就无法变为给定串。
那么合法串的条件即为“如果把所有长度 \(\geq A\) 的连续全 0 子串转为全 1 子串后,字符串中有长度 \(\geq B\) 的连续全 1 子串”
发现合法串特别难算,那么考虑容斥,计算非法串的数量。
把非法串的条件转化一下就是 由“长度 \(<A\) 的连续全 0 子串” 和 "长度 \(<B\) 的连续全 1 子串,其中允许将长度 $ \geq A$ 的连续全 1 子串转化为连续全 0 子串" 构成的串。
然后就可以 dp 了。
设 \(dp_{i,0/1}\) 为有 \(i\) 位字符,其中第 \(i\) 位字符为 \(0/1\) 时的方案数
\(dp_{i,0}=\sum_{j=1}^{A-1} dp_{i-j,1}\)
\(dp_{i,1}=dp_{i-1,0}+\sum_{j=2}^{B-1}dp_{i-j,0} \times g_{j-2}\)
为了防止第 \(i-j+1\) 中有 \(0\) 能够与第 \(i-j\) 位连接为子串,强制第 \(i-j+1\) 位为 1,而第 \(i\) 位也强制为 1,于是乘上的系数就是 \(g_{j-2}\) 而非 \(g_j\)
其中 \(g_j\) 为 \(j\) 个字符中仅允许拥有长度 $ \geq A$ 的连续全 0 子串,对 1 不作限制的方案总数。
这个也可以 dp 出来。具体可以看代码。
至于 \(A>B\) 的情况,其实只需将 0 1 翻转即可,计数过程如上。
代码如下:
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int mod=1e9+7;
int f[5005][2],g[5005],dp[5005][2];
signed main(){
int sum=0,ans=1;
int n,A,B;
cin>>n>>A>>B;
if(A>B) swap(A,B);
f[0][0]=f[0][1]=1;g[0]=1;
for(int i=1;i<=n;++i){
for(int j=A;j<=i;++j)
f[i][0]=(f[i][0]+f[i-j][1])%mod;
for(int j=1;j<=i;++j)
f[i][1]=(f[i][1]+f[i-j][0])%mod;
g[i]=(f[i][0]+f[i][1])%mod;
}
for(int i=1;i<n;++i){
if(i<A) dp[i][0]=1;
if(i<B) dp[i][1]=f[i][1];
for(int j=1;j<min(i,A);++j)
dp[i][0]=(dp[i][0]+dp[i-j][1])%mod;
for(int j=1;j<min(i,B);++j)
dp[i][1]=(dp[i][1]+dp[i-j][0]*((j<2)?1:g[j-2])%mod)%mod;
if(n-i<A) sum=(sum+dp[i][1])%mod; //后面全是0
if(n-i<B) sum=(sum+dp[i][0]*g[n-i-1]%mod)%mod; //后面是方案,防止重复往后面加一个 1 的分隔符
}
for(int i=1;i<=n;++i) ans=ans*2ll%mod;
ans=(ans-sum+mod)%mod;
cout<<ans;
return 0;
}
D - Lamps and Buttons
考虑 Snuth 的策略。即从小到大枚举 \(i\) 点灯,如果有暗灯变亮就转为点暗灯,直到无灯变亮为止。
如果枚举到一个 \(i\) 使得 \(p_i=i\),且这时未全灯点亮,则 Snuth 失败。
考虑 Snuth 胜利的条件,即在枚举到 \(i\) 使得 \(p_i=i\) 前全灯点亮。
那么可以枚举最前的 \(p_i=i\) 的位置,设这个位置为 \(t\)。如果没有 \(p_i=i ( 1\leq i \leq A)\),则 \(t=A+1\)
那么现在位置被划分成了三段,即 \([1,t-1]\),\([t+1,A]\),\([A+1,n]\) 注意这个第二段可能为空。设第一段长度为 \(x\),第二段长度为 \(z\),第三段长度为 \(y\)
要求第一段中不能有自环,第三段中所有数字位处置换环中至少有一个数字 \(<t\) 。第二段可以随便排列。
那么考虑加入置换环的方案数。先不考虑第一段中的条件,随便排列,方案是 \(x!\)
从小到大枚举第三段中的数字 \(i\),发现在置换环中可以插入第一段数字的左边,满足条件;也可以在置换环中插入前面的第三段中的数字的左边,因为前面的也满足条件,所以自身的条件也是满足的。因此对于每一个数字 \(i\),方案数为 \(x+i-1\)
从小到大枚举第二段中的数字 \(i\),发现所有已有数字都可以插入,所以方案数为 \(x+y+i\)
把这些方案乘起来,就是 \(\frac{x}{x+z}(x+y+z)!\)
但是如果这样做的话,第一段中可能有些数字会形成自环。可以考虑容斥,钦定 \(i\) 个点最后一定会变成自环,计算最后至少 \(i\) 个点会变成自环的方案数,然后就可以容斥。方案数即 \((-1)^i\binom x i \frac{x-i}{x+z-i}(x+y+z-i)!\)
代码如下:
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int mod=1e9+7,N=1e7+5;
int fac[N],inv[N],ins[N];
int ksm(int b,int n){
int res=1;
while(n){
if(n&1) res=res*b%mod;
b=b*b%mod; n>>=1;
}
return res;
}
void init(int n){
fac[0]=1;
for(int i=1;i<=n;++i)
fac[i]=fac[i-1]*i%mod;
inv[n]=ksm(fac[n],mod-2);
for(int i=n-1;i>=0;--i)
inv[i]=inv[i+1]*(i+1)%mod;
ins[1]=1;
for(int i=2;i<=n;++i)
ins[i]=(mod-(mod/i))*ins[mod%i]%mod;
}
int C(int n,int m){
if(n<m) return 0;
return fac[n]*inv[m]%mod*inv[n-m]%mod;
}
signed main(){
int n,A,sum=0,res;
cin>>n>>A;
init(n);
for(int t=2;t<=A+1;++t){
int x=t-1,y=max(A-t,0ll),z=n-A;
for(int i=0;i<=x;++i){
res=C(x,i)*(x-i)%mod*ins[x+z-i]%mod*fac[x+y+z-i]%mod;
if(i&1) sum+=(mod-res)%mod;
else sum+=res;
sum%=mod;
}
}
cout<<sum;
return 0;
}
E - Fragile Balls
设 \(P=\sum_{i=1}^m [a_i \not = b_i]\)
先考虑 \(c_i=1\) 的情况,那么答案要么是 \(P\) 要么是 \(-1\)
把 \((a_i,b_i)\) 看作一条无向边进行连边,那么考虑怎样的连通块内才是有解的。
由于题目中每个点的入度必然大于或等于 \(1\),因此不存在 \(DAG\),只存在如下三种连通块:
1.仅存在一个点的自环
2.连通块中仅包含一个长度 \(\geq 2\) 的环,并且不存在其他边
- 其他情况,即连通块的边数大于点数的情况,在这种情况下有多余的球搬到其他盒子
发现 \(c_i=1\) 时,如果存在第二种连通块,那么必然无解。
接着考虑 \(c_i \geq 1\) 的情况,如果存在第二种连通块也是有解的。
我们定义第二种连通块的数量为 \(X\) ,这样的一个连通块显然需要且只需要一个球,于是我们需要的贡献为 \(X\),并考虑达到这个贡献最少需要多少次浪费。显然每个第二种连通块需要的操作次数至少为 \(1\),于是答案即为 \(P+\)第二种连通块数量\(+\)最少浪费次数。
那么我们对于每种连通块上的球可以讨论一番:
1.球在自环上。这个球需要其他点的 \(1\) 次贡献来“解锁”,“解锁”后自身可以造成 \(c_i-1\) 次贡献,但是有 \(2\) 次浪费,一次浪费在球从其他点回来,一次浪费在其他球来这个点“解锁”。不过总体来看是造成 \(c_i-2\) 次贡献,因为他消费了其他点的 \(1\) 次贡献。这个点不“解锁”也没有关系。
- 球在环上。可以在这个环被处理的时候把该球移出去处理其他连通块然后再回来,总体来看是造成 \(c_i-1\) 次贡献,由于回来的次数已经算在了 \(P\) 上所以浪费了 \(0\) 次
3.球在第三种连通块上且 \(a_i \not = b_i\)。情况同上。
4.球在第三种连通块上且 \(a_i = b_i\)。可以造成 \(c_i-1\) 次贡献,浪费 \(1\) 次。
发现 \(2\) 情况与 \(3\) 情况是白给的,可以直接算。至于 \(1\) 情况和 \(4\) 情况的球可以用 two-points 计算,注意特判有没有球给 \(1\) 情况的球来“解锁”。
代码如下:
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int f[N],deg[N],sz[N],fl[N];
int find(int x){
return x==f[x]?x:f[x]=find(f[x]);
}
void merge(int x,int y){
x=find(x);y=find(y);
if(x==y) return;
f[x]=y; sz[y]+=sz[x];
}
void add(int x,int y){
merge(x,y);++deg[x];++deg[y];
}
int a[N],b[N],c[N];
vector<int> Y,Z;
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=n;++i)
f[i]=i,sz[i]=1;
for(int i=1;i<=m;++i){
cin>>a[i]>>b[i]>>c[i];
add(a[i],b[i]),--c[i];
}
for(int i=1;i<=n;++i)
if(deg[i]>2) fl[find(i)]=1;
int ned=0;
for(int i=1;i<=n;++i)
if(find(i)==i && !fl[i] && sz[find(i)]>=2) ++ned;
int baigei=0,flag=0;
for(int i=1;i<=m;++i)
if(c[i]>0){
if(fl[find(a[i])]){
if(a[i]==b[i]) Z.push_back(c[i]);
else flag=1,baigei+=c[i];
}
else{
if(a[i]==b[i]) Y.push_back(c[i]-1);
else baigei+=c[i];
}
}
sort(Y.begin(),Y.end(),greater<int>());
sort(Z.begin(),Z.end(),greater<int>());
for(int i=0;i<Y.size();++i) baigei+=Y[i];
int ans=1e9;if(ned==0) ans=0;
for(int i=0,j=Y.size()-1;i<=Z.size();++i){
while(j>=0 && baigei-Y[j]>=ned) baigei-=Y[j],--j;
if((flag || i) && baigei>=ned) ans=min(ans,2*(j+1)+i);
if(i<Z.size()) baigei+=Z[i];
}
if(ans==1e9) puts("-1");
else{
for(int i=1;i<=m;++i)
ans+=(a[i]!=b[i]);
ans+=ned;
cout<<ans;
}
return 0;
}
F - Division into Multiples
可以转化为 \(A,B,C\) 两两互质的情况,具体怎么搞可以看代码。
我们定义一个二元组 \((i,j)\) 是好的当且仅当 \(Ai+Bj \equiv 0 (\mod C)\) 并且没有一个二元组 \((i',j')\) 满足上一条件且 \((i' < i) \& (j'<j)\)
设 \(D =\frac{A}{B} \mod C\),那么满足第一个条件的二元组即为 \((i,C-Di)\)
那么问题变成挑出一些点 \((i,C-Di)\),要求对于任意 \(j<i\) 都有 \(Dj \mod C<Di \mod C\)
可以考虑一个高为 \(D\),长为 \(C\) 的循环网格,起始时点位于 \((0,0)\),之后点一直往 \((1,1)\) 的方向走,当 \(y=0\) 时,\((\frac{now}{D},C-x)\) 即为所求的好的二元组,其中 \(now\) 表示当前的移动次数。其实这个所谓的“循环网格”本质就是在枚举二元组中的 \(i\)。
考虑加速这一过程。若 \(W \geq H\),\(now=H,2H,3H,...,\lfloor\frac{W}{H}\rfloor \times H\) 都是要求的 \(now\)。把这些点以等差数列的形式表述即可。然后以类似欧几里得的方式,令 \(W=W \mod H,H=H \mod W\),即保留右上角的有用矩形。直到 \(H=0\) 为止。复杂度大概是 \(\mathcal{O}(\log H)\) 级别的。
根据求解过程,发现等差数列的 \(x\) 之差会不断变大,\(y\) 之差会不断变小,即 \(x_{i+1}-x_i \geq x_{i}-x_{i-1},y_{i+1}-y_{i} \geq y_{i}-y_{i-1}\),于是最优解的点组成了一个下凸壳。
那么问题变成把最优解的点取出一些组成一个集合 \(S\) ,要求 \(\sum_{i \in S}x_i \leq X,\sum_{i \in S} y_i \leq Y\),答案就是最大的 \(|S|\)
证明一下 \(\max \limits_{i \in S}\{i\}-\min\limits_{i\in S}\{i\} \leq 1\)
(注:该证明来自 \(\sf \color{black}{A} \color{red}{utumnKite}\))
设存在 \(i,j \in S\) 且 \(j-i \geq 2\),发现有 \(x_{i+1}-x_i \leq x_{j}-x_{j-1} \Rightarrow x_{i+1}+x_{j-1} \leq x_i+x_j\),\(y_{i+1}-y_i \leq y_{j}-y_{j-1} \Rightarrow y_{i+1}+y_{j-1} \leq y_i+y_j\)
所以去掉 \(i,j\),把 \(i+1,j-1\) 插入集合能让答案变得更加优秀。
假设一个等差数列上的点为 \((x_l,y_l),(x_l+\Delta x,y_l-\Delta y),...,(x_l+n\times \Delta x,y_l-n \times \Delta y)\)
那么一个点能被表示成 \((x_l+k \times \Delta x,y_l -(n-k) \times \Delta y)\)
二分答案 \(mid\),如果有一个点满足 \((x_l+k \times \Delta x) \times mid \leq X,(y_l -(n-k) \times \Delta y) \times mid \leq Y\),那么这个答案是肯定能被满足的。
稍微整理一下式子就能得出 \(check(mid)=\lfloor\frac{X-mid \times x_{l}}{\Delta x}\rfloor+\lfloor\frac{Y-mid \times y_l}{\Delta y}\rfloor \geq mid \times n\)
然后对于每一个等差数列二分答案即可。
代码如下:
#include<bits/stdc++.h>
using namespace std;
void exgcd(int a,int b,int &x,int &y){
if(b==0) return (void)(x=1,y=0);
exgcd(b,a%b,y,x);
y-=(a/b)*x;
}
int inv(int a,int mod){
int x,y;
exgcd(a,mod,x,y);
return (x%mod+mod)%mod;
}
int getY(int x,int C,int D){
return x==0?C:(C-1ll*x*D%C)%C;
}
void solve(){
int A,X,B,Y,C,g;
cin>>A>>X>>B>>Y>>C;
g=__gcd(A,B); A/=g; B/=g; C/=__gcd(g,C);
g=__gcd(A,C); A/=g; C/=g; Y/=g;
g=__gcd(B,C); B/=g; C/=g; X/=g;
A%=C;B%=C;if(C==1) return (void)(cout<<X+Y<<endl);
int D=1ll*A*inv(B,C)%C;
int W=C,H=D,now=0,invD=inv(D,C),tmp;
vector<int> pos,cnt; //等差数列的起始值与点的数量
while(W){
H=(H-1)%W+1;tmp=W/H;
pos.push_back(1ll*now*invD%C);
cnt.push_back(tmp);
now+=tmp*H;W-=tmp*H;
}
pos.push_back(C);
long long ans=0;
for(int i=0;i<cnt.size();++i){
int lx=pos[i],ly=getY(lx,C,D);
int rx=pos[i+1],ry=getY(rx,C,D);
int del_x=(rx-lx)/cnt[i],del_y=(ly-ry)/cnt[i];
long long mid,l=0,r=X+Y,res=0;
while(l<=r){
mid=(l+r)>>1;
long long p=(X-mid*lx),q=(Y-mid*ry);
if(p>=0 && q>=0 && p/del_x+q/del_y>=mid*(cnt[i])) res=mid,l=mid+1;
else r=mid-1;
}
ans=max(ans,res);
}
cout<<ans<<endl;
}
signed main(){
int T;cin>>T;
while(T--) solve();
return 0;
}
AGC044 题解
A - Pay to Win
考虑倒着做,即 \(N \rightarrow 1\) 的最小代价。
那么考虑每次操作后 \(N\) 会变为 \(\lfloor\frac{N}{k}\rfloor\) 或者 \(\lceil\frac{N}{k}\rceil\) ,其中 \(k \in \{2,3,5\}\) ,所以可以直接枚举 \(k\) 嗯算,再加个优先队列+最优性剪枝可以跑得很快,大概是 3 只 \(\log\) 的水平。
B - Joker
考虑每个点走人后跑最短路。由于每个点的到达离开影院的最短路之和是 \(n^3\) 级别的所以能过
C - Strange Dance
第一种操作:同 CF1401F
第二种操作:同 [省选联考 2020 A 卷] 树
由于不会写代码就直接边贺边写了,代码就不放了
D - Guess the Password
可以先询问字符串 \(S=128\) 个字符 \(ch\),从而得出 \(ch\) 在密码串中的数量,从而得出密码串的长度。
然后有一个结论就是,如果 \(T\) 是 \(S\) 的子序列,那么 \(S\) 到 \(T\) 的编辑距离为 \(|S|-|T|\),就可以用这个来判断一个字符串是不是密码串的子序列。
可以考虑对字符集分治,\(merge(l,r)\) 表示仅保留字符大小为 \(l \sim r\) 的字符后的密码串。
就可以用归并排序做了。设 \(A=merge(l,mid),B=merge(mid+1,r)\)
那么如果要把 \(a_i\) 先插入答案字符串,首先就要判断 \(b_{j \sim len_b}\) 是否群体在 \(a_i\) 之后,这一点可以用前面的那个结论来判断。
其他就很简单了。由于代码也是贺的所以就不放了
E - Random Pawn
先考虑下弱化版:https://www.luogu.com.cn/problem/P5155
先考虑一个点 \(x\) ,随机 \(+1,-1\) 后在 \(0,L\) 停止,在 \(L\) 停止的概率。
设这个概率为 \(g_x\),有 \(g_0=0,g_L=1,g_x=\frac{g_{x-1}+g_{x+1}}{2}\),发现这是一个等差数列的形式,即 \(g_{x}=\frac{x}{L}\)
那么一个点 \(x\) 的答案就是 \(\max\limits_{a \leq i \leq b}\{v_a \times \frac{b-i}{b-a} +v_b \times \frac{i-a}{b-a}\}\)
发现这个东西就是线段 \((a,v_a)(b,v_b)\) 与直线 \(x=i\) 交点的纵坐标。
容易得出答案的点必定是在凸包上离 \(i\) 最近的两点。
其实还有另一个推导方式,那就是设 \(f_x\) 为在这个点停止的最大期望值。
\(f_x=\max\{\frac{f_{x-1}+f_{x+1}}{2},a_x\}\)
然后就跟上面差不多了。
考虑这个题怎么做。由于在最大点肯定会停所以直接以最大点为起点破环成链。
但是在这个题里 \(f_x=\max\{a_x,\frac{f_{x-1}+f_{x+1}}{2}-B_x\}\)
考虑构造一个 \(g_x=\max\{a'_x,\frac{g_{x-1}+g_{x+1}}{2}\}\),设 \(d_x=f_x-g_x\)
\(g_x=f_x-d_x=\max\{a_x-d_x,\frac{f_{x-1}-d_{x-1}+f_{x+1}-d_{x+1}}{2}-B_x-d_x\}\)
发现 \(d_{i+1}=2 \times d_i -d_{i-1} +2 \times B_i\) 的时候可以构造。
接下来的步骤和那个弱化版其实已经差不多了,直接做
顺便一提样例萎了其实也能过题
AGC043
看题解只看会了 A,B,C,D 的菜鸡来写题解了
A - Range Flip Find Route
结论:答案是从左上角往右下角走路,最少的 # 连续段的数量。
然后可以直接 bfs 了。
B - 123 Triangle
由于所有数字减一对答案无影响,所以把每个数字都减去一,考虑起来可以更加方便。
考虑部分分,\(a_i\in \{0,1\}\) 的时候怎样做。
发现当 \(a_i \in \{0,1\}\) 时,\(|a_i-a_{i+1}|=a_i \oplus a_{i+1}\),那么直接考虑每个数字出现的次数即可。对于每个 \(i\),\(a_i\) 出现的次数是 \(\binom {n-1} {i-1}\),直接计算即可。
考虑当 \(a_i \in \{0,1,2\}\) 时怎么做。由于 \(|1-2|=1,|2-1|=1,|1-0|=1,|0-1|=1\),所以如果不是全 \(1\) 的情况下必然下一行会有一个 \(1\),并且所有的 \(2\) 必定会被某一个 \(1\) 减成 \(1\)。
那么问题直接转化成 \(a_i \in \{0,1\}\) 时的情况。
如果 \(a_i \in\{0,2\}\) 的话,发现和 \(a_i \in \{0,1\}\) 时是一样的。同上述计算即可。
C - Giant Graph
由于选一个三元组 \((i,j,k)\) 能抵上所有的 \((i',j',k') \ (i'+j'+k' < i+j+k)\) 之和,所以直接贪心选最大即可。
考虑一个三元组 \((x,y,z)\) 是否能取,设 \(f_{x,y,z}\) 为这个三元组是否可以取。
显然有状态转移 \(f_{x,y,z}=\prod\limits_{x'+y'+z' >x+y+z} [f_{x',y',z'}=0]\),其中 \((x',y',z')\) 与 \((x,y,z)\) 有边。
时间复杂度 \(\mathcal{O}(n^3)\) ,必然会 \(\sf TLE\)
那么考虑这个连边是怎么连的。当存在边 \(x_i \rightarrow x_j\) 时,对于任意 \(y,z\) 有 \((x_i,y,z) \rightarrow (x_j,y,z)\),其他图的情况下同理。
如果把无向图变为从小权点连向大权点的 DAG 的话,那么 \((x,y,z) \rightarrow (x',y',z')\) 看上去就像是三张图上的 \(x,y,z\) 三个点,选中一个点走一条出边后变成 \(x',y',z'\) 三个点。
再联系一下这个转移方程,发现就是一个经典的博弈论问题:给定三张图上的三个点,玩家每一次操作可以选中三个点中的其中一个,令其走向选中的一条出边,无法移动者输。现在 Alice 和 Bob 轮流移动一次,问对于每一个状态 \((x,y,z)\),是 Alice 赢还是 Bob 赢。
决定这个胜负状态的是 SG 函数,如果三个点的 SG 函数的异或和为 0 ,那么先手必败,否则先手必胜。由于不能走的情况下 \((x,y,z)\) 是可以取的,所以如果一个三元组是先手必败的情况,那么这个三元组就是可以取的。
具体怎么做,对于每一张图,计算每个数字对 SG 函数的贡献,最后枚举一下 SG 函数的值即可。由于 SG 函数的大小范围在 \(\sqrt{m}\) 内所以复杂度是对的。
D - Merge Triplets
如果一个点不是前缀最大值的话,那么显然它和前面一个数字组成一组。
如果有长度为 \(1\) 的组数大于或等于长度为 \(2\) 的组数,那么显然我们是可以构造出一种方案的。长度为 \(3\) 的组不怎么影响。所以设长度为 \(1\) 的组的贡献为 \(1\),长度为 \(2\) 的组的贡献为 \(-1\),长度为 \(3\) 的组的贡献是 \(0\), dp 出贡献为正整数的方案数即可。
问题变成,钦定某些点 \(a_{r_i}\) 为 \([1,r_i]\) 的最大值,有多少种排列的方案。
对于 \(i=1\) 的情况,显然有 \(\binom {n}{r_i} \times (r_i-1)! \times (n-r_i)!=\frac{n!}{r_i}\) 种方案
对于 \(i=2\) 的情况,设 \(r_1<r_2\),显然也有 \(\binom {n}{r_2} \times (n-r_2)! \times \frac{r_2!}{r_1}=\frac{n!}{r_1r_2}\) 种方案。
方案数即为 \(\frac{n!}{\prod\limits_{i}r_i}\)
在 dp 的时候通过乘系数来顺便计算一下这个即可。
E - Topology
不会
F - Jewelry Box
不会
AGC041
A
不想讲
B
也不想讲
C
手玩出 n=4,n=5,n=6,n=7 ,发现都有构造方案满足每行每列多米诺骨牌有且仅有 2 个,然后就可以把上述四个矩阵与全 . 矩阵瞎拼几下就能拼出 \(n \ge 4\) 时的方案。
发现 n=1,n=2 的情况不可做, n=3 特判即可。
D
考虑 \(n\) 为奇数的情况
就是限制 \(\sum_{i=1}^{\frac{n+1}{2}}a_i > \sum_{i=\frac{n+1}{2}+1}^n a_i\)
考虑一下差分 \(a\) 后的 \(b\),设 \(b_0=1\),满足了 \(a_i \ge 1\) 的限制
\(\sum_{i=1}^{\frac{n+1}{2}} (\sum_{j=1}^i b_j+1) > \sum_{i=\frac{n+1}{2}+1}^n (\sum_{j=1}^i b_j+1)\)
\(\sum_{i=1}^{\frac{n+1}{2}} \sum_{j=1}^i b_j \geq \sum_{i=\frac{n+1}{2}+1}^n\sum_{j=1}^i b_j\)
\(2 \sum_{i=1}^{\frac{n+1}{2}} \sum_{j=1}^i b_j \geq \sum_{i=1}^n \sum_{j=1}^i b_j\)
\(2\sum_{i=1}^{\frac{n+1}{2}}b_i \times (\frac{n+1}{2}-i+1) \geq \sum_{i=1}^n b_i \times (n-i+1)\)
然后减一减就有了
\(\sum_{i=1}^n b_ic_i \leq 0\)
其中 \(c_i=\begin{cases}i-2 \ (1 \leq i \leq \frac{n+1}{2}) \\ n-i+1 \ (otherwise) \end{cases}\)
发现只有 \(c_1 =-1\),而 \(c_i \ge 0,b_i \ge 0 \ (i \not = 1)\)
于是就有 \(b_1 \geq \sum_{i=2}^n c_ib_i\)
而根据 \(a_n \leq n\),有 \(\sum_{i=1}^n b_i+1 \leq n\),有 \(b_i \leq n-\sum_{i=2}^nb_i -1\)
诶于是对于一组 \(b_{2 \dots n}\), \(b_1\) 有 \(n-\sum_{i=2}^n(c_i+1)b_i-1\) 个解。
所以可以直接对 \(\sum_{i=2}^n b_ic_i\) 进行 dp ,对于一组解 \(\sum_{i=2}^n b_i(c_i+1)=j\),这组解对答案有 \(n-j-1\) 的贡献。
\(\sf\color{black}{F}\color{red}{roggy}\):这题就是个傻逼完全背包
果然这就是强者吗 /kk
E
- \(\rm Task \ 1\)
连我都会做,相信各位读者也会做,不讲
- \(\rm Task \ 2\)
从后往前考虑每根管道的方向,设 \(fin_i\) 为 \(i\) 流向的终点, \(cnt_i\) 表示流向 \(i\) 的管道有多少条
那么考虑 \(cnt_{fin_{x_i}}\) 与 \(cnt_{fin_{y_i}}\) 的大小即可。如果 \(cnt_{fin_{x_i}} \leq cnt_{fin_{y_i}}\) 则令 \(y_i \rightarrow x_i\),反之 \(x_i \rightarrow y_i\)。显然这样构造是不会令任何一个 \(cnt_i \ge n\) 的。
F
不会
AGC040
A
拓扑序搞一搞就行
B
分类讨论,设 \(L=\max\limits_i \{L_i\},R=\min\limits_i \{R_i\}\)
- 如果 \(L\) 与 \(R\) 的对应区间属于同一集合 \(S\)
那么无论什么区间加入 \(S\),答案都不变,仅需考虑如何让另一个集合的答案最大。那么显然就是最长的那一段区间的长度。
- 如果不是
答案即求最大的 \(\min\limits_{i \in S} \{R_i\}-\max\limits_{i \in S} \{L_i\}+\min\limits_{i \not \in S} \{R_i\}-\max\limits_{i \not \in S} \{L_i\}\)
枚举一下最大的 $\max\limits_{i \in S}{L_i} $ 即可(\(L \not =\max\limits_{i \in S}\{L_i\}\)),而 \(\max\limits_{i \not \in S}\{L_i\}\) 显然就是 \(L\)
于是把区间按 \(l_i\) 排序,剩下两个前后缀 \(\min\) 搞一搞即可
C
可以把偶数位置的 \(A\) 变成 \(B\),把 \(B\) 变成 \(A\) ,显然这样转化过的串与原串成映射关系。
那么限制从 AB,BA,变为了 AA,BB
显然如果 A 或 B 的数量大于串长的一半,这个串是无法被删为空串的,因为无论怎么删都会留下全为 A 或 B 的串
考虑容斥计算这些不合法的串,答案即为
\(3^n - \sum_{i=\frac{n}{2}+1}^n \binom n i \times 2^{n-i} \times 2\)
(后面式子的意义:选出 i 个字符钦定为 A 或 B,其他 n-i 个字符随便选 BC/AC ,因为钦定方案有两种所以乘 2)
D
不会
E
设 \(1\) 操作的贡献为 \(c_i\) ,那么答案就是求最小的 \(\sum_{i=2}^n [c_i < c_{i-1}] + [a_{i-1}-c_{i-1}<a_i-c_i]\)
转化一下就是求 \(\sum_{i=2}^n [c_i-c_{i-1}<0] + [c_i -c_{i-1} <a_i-a_{i-1}]\)
考虑 dp,设 \(f_{i,j}\) 为 \(c_i=j\) 时前 \(i\) 个位所造成的最小代价。
发现当 \(f_{i,k} >f_{i,j}+2\) 时,这个 \(k\) 显然无用
而 \(f_{i,j} =f_{i,k} \ (j <k)\) 时,这个 \(k\) 也是无用的,因为 \(j\) 转移时造成的代价更小。
于是可以考虑去掉无用状态,令 \(f_{i,j}\) 为最小代价为 \(j\) 时的最小 \(c_i\)
状态用 map 存储,转移时分类讨论即可。时间复杂度大致为 \(\mathcal{O}(n \log n)\)
代码参考了 \(\sf \color{black}{Z}\color{red}{hou \_ JK}\)
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
void upt(map<int,int> &f,int j,int v){
if(!f.count(j)) f[j]=v;
else f[j]=min(f[j],v);
}
map<int,int> f[N];
// f_{i,j} 表示代价为 j 时,最小的状态 c_i 是多少.
int n,a[N];
signed main(){
cin>>n;
for(int i=1;i<=n;++i)
cin>>a[i];
f[1][0]=a[1]; f[1][1]=0;
for(int i=2;i<=n;++i){
for(auto [v,j]:f[i-1]){
if(f[i-1].begin()->first < v-2) break;
if(j+min(a[i]-a[i-1],0)>0) upt(f[i],v+2,0);
if(j+min(a[i]-a[i-1],0)<=a[i]) upt(f[i],v+1,max(0,j+min(a[i]-a[i-1],0)));
if(j+max(a[i]-a[i-1],0)<=a[i]) upt(f[i],v,j+max(a[i]-a[i-1],0));
}
}
int ans=1e9;
for(auto [v,j]:f[n])
ans=min(ans,v+(j!=0));
cout<<ans;
return 0;
}
F
可以去看一下 \(\sf \color{black}{A}\color{red}{utumn \_ Kite}\) 的博客,讲得很清晰
AGC039
A
容易发现一个长为 \(X\) 的连续相同子串对答案的贡献为 \(\lfloor \frac{X}{2} \rfloor\)
顺便特判一下末尾的连续相同串与起始的连续相同串的情况即可。
B
枚举 bfs 树的根 \(u\) ,通过 \(u\) 对每个点的最短距离来分层即可。
顺便判断一下是否有奇环的情况,如果有的话那么显然无解。
C
操作可以看成是把最后一个数字反转后插入至第一位,那么 \(x\) 次操作就相当于把一个长度为 \(x\) 的后缀插入到前面。
所以一个数能变回去当且仅当这个数形如 \(SS'SS'...S\) ,其中 \(S'\) 为 \(S\) 每位字符反转后的结果。
可以枚举一下 \(S\) 的长度然后直接计数就行了
但是发现这样会算重,所以加上一重容斥就行了。
代码: code
D
不会
E
感觉 Autumnkite 和 Froggy 写得挺好的,可以去看一看
F
感觉 PinkRabbit 写得挺好的,可以去看一看
AGC037
A
显然一个字符串能分成若干个长度为 \(1\) 或 \(2\) 的串。
考虑 dp,\(f_{i,1/2}\) 表示以 \(i\) 结尾的串长度为 \(1/2\) 的答案
转移就很显然了
B
感觉跟 Japanese Student Championship 2019 Qualification 的 C 题很像啊
发现选择方式是固定了之后就可以做了
考虑如何操作,设这个球的颜色是 \(R\),其他情况下同理
如果有 \(GB\) 串或者 \(BG\) 串的话,且这些串没有在前面被匹配掉,那么就把这个球跟这个串匹配
否则从 \(G\) 字符或 \(B\) 字符里选一个没有在前面被匹配掉的。
方案数挺明显的
C
考虑倒着做,发现不可能在最大数被操作之前做相邻两个数字,且最大值被操作之后对其他数字没有影响。
所以直接挑出最大数搞一搞就行了。
D
可以考虑 \(C\) 矩阵要怎样才合法。
考虑给每个点 \(a_{i,j}\) 染色 \(c_{i,j} = \lfloor\frac{a_{i,j}-1}{m}\rfloor +1\)(即这个点在所求矩阵里属于的行),那么这个 \(C\) 矩阵里第 \(i\) 行的所有数字肯定是第 \(i\) 种颜色的
那么考虑 \(B\) 矩阵要咋搞才能到这个 \(C\) 矩阵
再考虑染色,\(B\) 矩阵里每一列的元素在颜色来看肯定是一个长为 \(n\) 的排列
再考虑怎么从 \(A\) 矩阵到达 \(B\) 矩阵
对于每一列,直接对行跟颜色跑二分图完美匹配即可。根据 \(Hall\) 定理可证一定有解。
E
把原串 \(S\) 与反串 \(S'\) 拼接成一个新串 \(T\),考虑这个 \(T\) 里长度为 \(n\) 的子串接下来 \(k-1\) 次如何操作更好
如果这个子串末尾是 \(T\) 中字典序最小的字符 \(ch\) 的话,那么稍微手玩一下就能得出能令这个子串的开头变为仅由 \(ch\) 构成的长为 \(\min\{n,2^{k-1}\}\) 的串。
如果末尾连续相同字符有 \(L\) 个的话,那么长度可以变为 \(\min \{n,2^{k-1} \times L\}\)
如果这个子串末尾不是 \(T\) 中字典序最小的字符,那么肯定是不合法的,可以直接剔除。
具体细节看代码。
F
不会做
AGC036
A - Triangle
设 \(A=(X_1,Y_1),B=(X_2,Y_2),C=(X_3,Y_3)\)
那么 \(S= \overrightarrow{AB} \times \overrightarrow{AC}\)
考虑把 \(A\) 点放在原点,那么 \(S=\overrightarrow{AB} \times \overrightarrow{AC}=X_2Y_3-X_3Y_2\)
发现任意正整数 \(i \ (i \le 10^{18})\) 都能表示成 \(10^9k-b\ (k,b\le 10^9)\) 的形式,所以可以构造 \(X_2=10^9,Y_2=1\),至于 \(X_3,Y_3\) 就很显然了
B - Do Not Duplicate
发现可以找循环节。显然,循环节的数量不超过 \(\mathcal{O}(n)\)
手动模拟这个过程,对于第 \(i\) 位记录最小的 \(j\),使 \(a_j=a_i\) 且 \(j>i\),如果没有这个 \(j\) 那么就令 \(j\) 等于使 \(a_j=a_i\) 的最小的 \(j\)。
那么模拟过程的时候可以令位置 \(p=pos_p+1\),如果 \(pos_p<p\) 的话那么就说明模拟了一次过程。直到 \(p=n+1\),这时候说明已经找到了循环节,直接退出。
找到循环节之后 \(k\) 变为 \(n\) 级别,接下来直接模拟即可。
C - GP 2
发现一个数列如果要合法的话必须满足如下性质:
对于第二种限制,可以枚举奇数的个数 \(k\) 然后用隔板法计算 \(+2\) 的分配
对于第三种限制,可以容斥,枚举最高值 \(j \in [2 \times M+1,3 \times M]\),由于第一种限制,只能有一个 \(a_i=j\)
D - Negative Cycle
由于要求删边后不存在负环,所以删边后的图可以跑最短路,设 \(p_i\) 为删边后的图 \(1\) 到 \(i\) 的最短路。
由于有边权为 \(0\) 的 \(i \rightarrow i+1\),所以 \(p_i-p_{i+1} \ge 0\)
设 \(q_i=p_i-p_{i+1}\),有 \(q_i \ge 0\)
\(q_i=1\) 是可以有的,比如说边权为 \(-1\) 的 \(i \rightarrow i+1\)
但 \(q_i=2\) 时,没有删边后的图能构造出这种情况,手玩得知当 \(q_i=2\) 时,必然会产生负环。
所以 \(q_i \in \{0,1\}\)
对于 \(i \rightarrow j\) 的边权为 \(1\) 时,有 \(p_i+1 \ge p_j\),也即 \(\sum_{k=i}^{j-1} q_k \le 1\)
对于 \(i \rightarrow j\) 的边权为 \(-1\) 时,有 \(p_i-1 \ge p_j\),也即 \(\sum_{k=i}^{j-1} q_k \ge 1\)
也就是说,当 \(\sum q_i=0\) 时,对应的边权为 \(-1\) 的边必须删除
而 \(\sum q_i \ge 2\),也就是至少有两个 \(q_i=1\) 时,对应的边权为 \(1\) 的边必须删除
可以对 \(q_i\) 权值为 0 的连续段 dp,设 \(f_{i,j}\) 表示前 \(i\) 个点,第 \(j+1\) 个点和第 \(i\) 个点组成一个权值为 0 的连续段的最小代价
或者可以手玩,手玩发现最短路 \(p_i\) 随着 \(i\) 的变大而递减,且递减大小不超过 \(1\),可以把最短路大小相同的数字看作一个段。
手玩发现如果 \(p_i-p_j=2\) 的话,那么不能有边权为 \(1\) 的 \(j \rightarrow i\),否则会有负环。
然后发现可以对段 dp,代价的话就是减去连向非相邻段的 \(1\) 边,还有自身段内部连接的 \(-1\) 边的权值。
其实跟上面是差不多的。
E - ABC String
先把极长的连续相同字符缩成一个字符,满足相邻字符不同的限制。可以用链表来维护这个相同字符串。
设 \(A,B,C\) 的出现次数为 \(cnt_A,cnt_B,cnt_C\)
不失一般性地,我们设 \(cnt_A \le cnt_B \le cnt_C\)
为了令最后 \(cnt_A=cnt_B=cnt_C\) ,我们必然要删去几个 \(C\) ,令最后 \(cnt_B=cnt_C\)
首先如果有 \(C\) 两边的字符不同的话,那么删掉这个 \(C\) 对答案没有影响,直接删除即可
如果还是不行的话,那么如果有 \(C\) 两边的字符全为 \(A\) 的话,那么显然要删掉这个 \(C\) ,这时 \(cnt_C=cnt_C-1,cnt_A=cnt_A-1\)
如果删完后有 \(cnt_C > cnt_B\) 那么必然无解,否则 \(cnt_A \le cnt_B =cnt_C\)
可以通过删除形似 BC / CB 的串来让 \(cnt_A=cnt_B=cnt_C\)
如果这个串的左右均不为 A 的话,那么显然就可以删除,最后串的形式类似于 ABCACBACABA....A,显然这时 \(cnt_A>cnt_B ,cnt_A>cnt_C\),那么在删除的过程中一定有 \(cnt_A=cnt_B=cnt_C\),找出这个时刻即可。
F - Square Constraint
题面可以转化为:
满足下列条件的排列 \(P\) 有多少个?
- 对于 \(\forall i\),有 \(l_i \le p_i \le r_i\)
然后发现这个问题是个 npc 问题...
发现对于任意 \(i \ge n\),有 \(l_i=0\)
然后可以引出这样的一个问题:
- 对于 \(\forall i\),有 \(0 \le p_i \le R_i\),求问满足这样要求的排列 \(P\) 有多少个?
显然把 \(r_i\) 排序后,方案数为 \(\prod_{i=0}^{n-1} (R_i-i+1)\)
但是对于 \(i \le n\),\(l_i \not =0\),所有数字必须大于或等于 \(l_i\)
于是考虑容斥,钦定 \(i\) 个数字不合法,把这些不合法的数字的 \(R_i\) 设为 \(l_i-1\),其他数字的 \(R_i\) 设为 \(r_i\),排序一波就能得到一个 \(\mathcal{O}(2^n n \log n)\) 的优秀做法
研究一下,发现 \(l_i \ge l_{i+1},r_i \ge r_{i+1},l_0 < r_n\)
于是就有 \(l_{2n-1} \le l_{2n-2} \le ... \le l_0 < r_n \le r_{n-1} \le r_{n-2} \le ... \le r_0\)
于是我们得到了一个 不需要排序 的做法,不管是合法数字还是不合法数字还是位置大于等于 \(n\) 的数字都能轻松得到其 \(R_i\) 的名次。
然后考虑把这些数字排序,当 \(i \ge n\) 的时候按 \(r_i\) 排序,否则按 \(l_i-1\) 排序
由于名次算起来很轻松,所以考虑 dp,\(f_{i,j}\) 表示前 \(i\) 个数字,钦定 \(j\) 个数字是不合法数字时的方案数。
由于转移方程较为复杂所以直接给代码:
l=2*n-1; r=2*n-1;
for(int i=0;i<=2*n-1;++i){
while(i*i + l*l >= n*n && l>=0) --l;
while(i*i + r*r > 4*n*n && r>=0) --r;
if(l==-1) a[++cnt]=make_pair(r+1,0);
else a[++cnt]=make_pair(l+1,r+1);
}
sort(a+1,a+cnt+1);
for(int k=0;k<=n;++k){
memset(f,0,sizeof(f));f[0][0]=1;
for(int i=1,F=0,g=0;i<=cnt;F+=(a[i].second!=0),g+=(a[i].second==0),++i)
//F表示 i < n 的数的个数,g表示 i >= n 的数的个数
for(int j=0;j<=k;++j){
int now=f[i-1][j];
if(a[i].second==0) add(f[i][j],mul(now,a[i].first-g-j));
//a[i].second == 0 表示对应的位置 >= n ,然后 g+j 表示排名 , 在下界上相当显然 , 在上界上则是因为 r_i 递减
else{
if(j!=k) add(f[i][j+1],mul(now,a[i].first-g-j));
// 同上
add(f[i][j],mul(now,a[i].second-(F-j)-k-n));
// k+n+(F-j) 表示排名,n是因为 r_i 递减,k是因为上面那个很长的不等式,(F-j)是因为排序
}
}
if(k&1) add(ans,mod-f[cnt][k]);
else add(ans,f[cnt][k]);
}
AGC035
A - XOR Circle
有 \(a_i=a_{i-1} \oplus a_{i+1} \Rightarrow a_{i-1}=a_i \oplus a_{i+1}\)
那么 \(a_i=a_{i+1} \oplus a_{i+2}\)
那么 \(a_{i-1}=a_{i+2}\)
得出结论:仅有 \(\forall i,a_{i}=a_{i+3}\) 时,才能满足题中的条件。
讨论一下等于 \(a_1\) 的数字有多少个,也就相当于从一个长为 \(n\) 的环上,以 \(1\) 为起点开始走,问几步之后能再度回到 \(1\)
这其实就相当于问置换环的大小,显然大小就是 \(\frac{n}{\gcd(n,3)}\)
然而由于 \(3\) 是一个质数,所以置换环大小要么是 \(\frac{n}{3}\) 要么是 \(n\)
于是得出结论:
-
如果 \(n \bmod 3 \not = 0\),那么置换环大小为 \(n\),判断所有数字是否全为
0,如果不是则为No,否则则为Yes -
如果 \(n \bmod 3 = 0\) ,那么置换环大小为 \(\frac{n}{3}\),这个时候需要判断三种情况:1.全为
0,显然合法,答案为Yes。2.有 \(\frac{n}{3}\) 个数字是0,其他数字相同,显然合法,答案为Yes3.有且只有 \(3\) 种数字,且数字出现次数都为 \(\frac{n}{3}\),设第一种数字为 \(A\),第二种数字为 \(B\),其余数字为 \(C\),假如 \(A \oplus B=C\),那么合法,答案为Yes
B - Even Degrees
如果边数为奇数显然不合法,因为如果所有点的出度为偶数,那么边数为偶数。偶数的情况下可以证明一定有解。
以生成树为基础进行构造,不在生成树上的边可以随便构造,其他则根据奇偶性构造。
C - Skolem XOR Tree
先想怎样才是无解,发现如果 \(n\) 可以表示成 \(2^i\) ,那么显然没有走其他数字的方式能构造这一位,必然无解。否则可以证明有解。
考虑到 $2i \oplus 2i+1 =1 $ ,直接构造边 \((1,2i),(1,2i+1),(2i+1,2i+n),(2i,2i+n+1)\),就可以同时满足 \(2i\) 与 \(2i+1\) 。
再考虑 \(1\) 的情况怎么办,可以不让 \(2\) 与 \(3\) 按上述方式连边,而是仿照样例里的方式连边,这样就可以满足 \(1\)
再考虑如果 \(n \bmod 2 =1\),匹配不上数字的情况。把连接 \(1\) 的两个数字挑出来,设这两个数字为 \(i\) 和 \(j\),如果 \(i \oplus j \oplus 1 =n\),那么可以通过构造边 \((i,n),(j,n+n)\) 的方式满足 \(n\)
D - Add and Remove
设 \(f_{l,r}\) 为把 \([l,r]\) 区间删除到只剩 \(l,r\) 后的最小值,发现转移不来
为了转移,我们考虑每个数字被取后会怎样造成贡献。枚举 \([l,r]\) 的中转点 \(i\),如果把 \([l,i]\) 区间删除至只剩 \(l,i\),把 \([i,r]\) 区间删除至只剩 \(i,r\) 的代价最小值算出来后,显然只需要考虑 \(a_i\) 之后会被算多少次。
发现如果 \(a_l\) 被算 \(c_l\) 次,\(a_r\) 被算 \(c_r\) 次的话,那么 \(a_i\) 会被算 \(c_l+c_r\) 次。而且 \(a_1,a_n\) 仅会被算一次。
于是可以设 \(f_{l,r,c_l,c_r}\) ,表示把 \([l,r]\) 区间删除到只剩 \(l,r\) ,且 \(a_l\) 之后会算 \(c_l\) 次,\(a_r\) 之后会算 \(c_r\) 次的最小值,\(i\) 的贡献就是 \((c_l+c_r) \times a_i\)
有转移方程如下:
E - Develop
把点 \(x\) 朝 \(x+k\) 与 \(x-2\) 连边,可以发现如果选出的点集不包括环,那么这个点集是可以按拓扑序删除的。
所以合法的选出点集仅有不包含环这一限制。
考虑 \(k\) 是偶数的时候怎么做,显然奇数点和偶数点选出的方案是互相独立的,可以直接乘起来,仅需考虑对于奇数点/偶数点选出的方案怎么做。
奇数点的情况就是可以选点,但是不能选出连续 \(\frac{k}{2}+1\) 个点,简单 dp 即可。偶数点的情况同理。
那么考虑 \(k\) 是奇数的时候怎么做。发现这个环的形式类似于 \(a \rightarrow a-2i=b-k \rightarrow b \rightarrow a-k \rightarrow a\),手玩一下发现长度为 \(k+2\)
如图,把奇数点 \(x\) 放在左边,把偶数点 \(y\) 放在右边,同一层的点满足 \(x+k=y\),那么这个限制即为:若干条往上边+一条右边+若干条往上边的长度 \(\le k+1\)
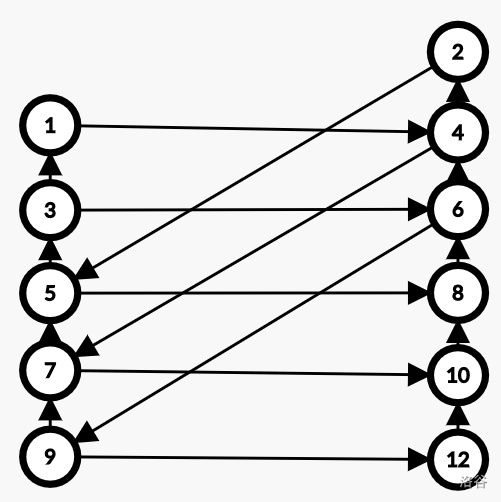
那么考虑 dp,设 \(f_{i,j,k}\) 为考虑前 \(i\) 层点,其中形如从左部点走若干条往上边+一条右边+若干条往上边的最长链长度为 \(j\),且从第 \(i\) 个右部点走若干条往上边的最长链长度为 \(k\) 的方案数。
转移见代码。
F - Two Histograms
发现方案重复当且仅当出现了这种涂色方法:
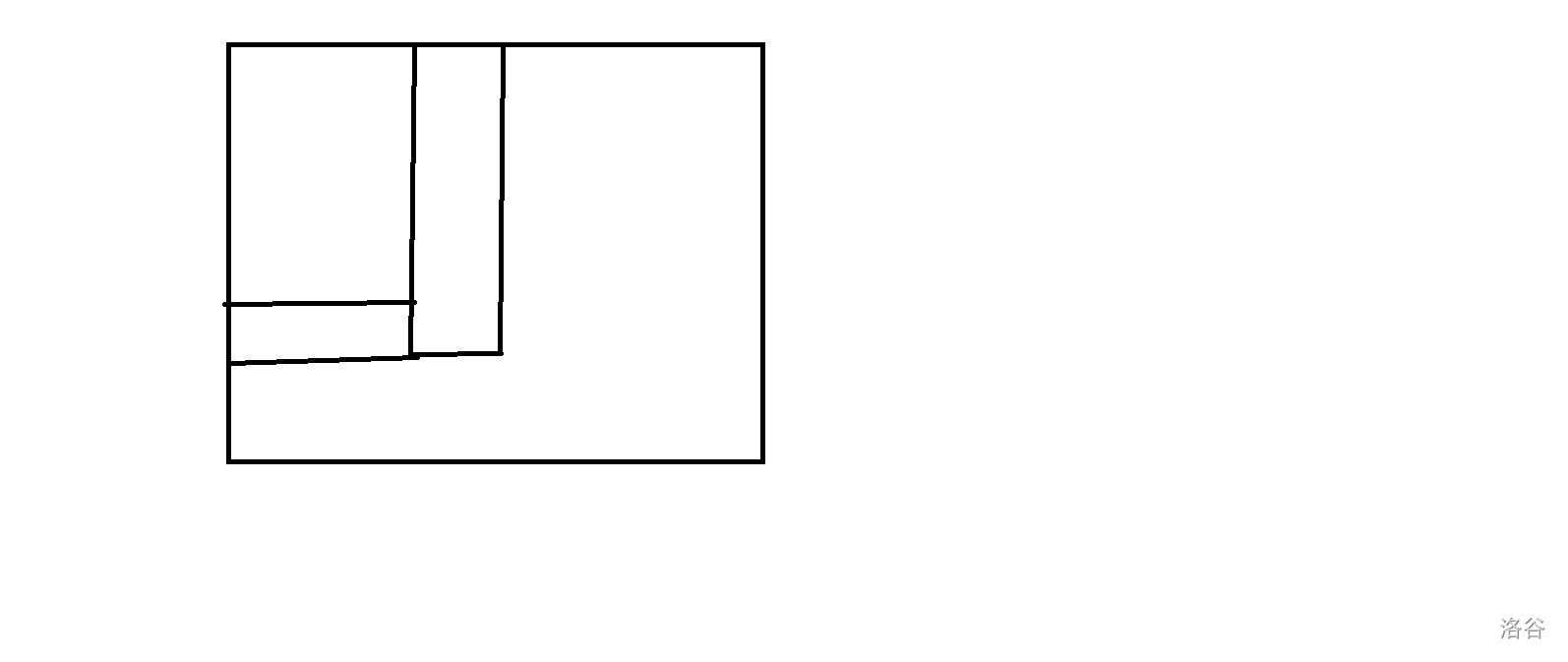
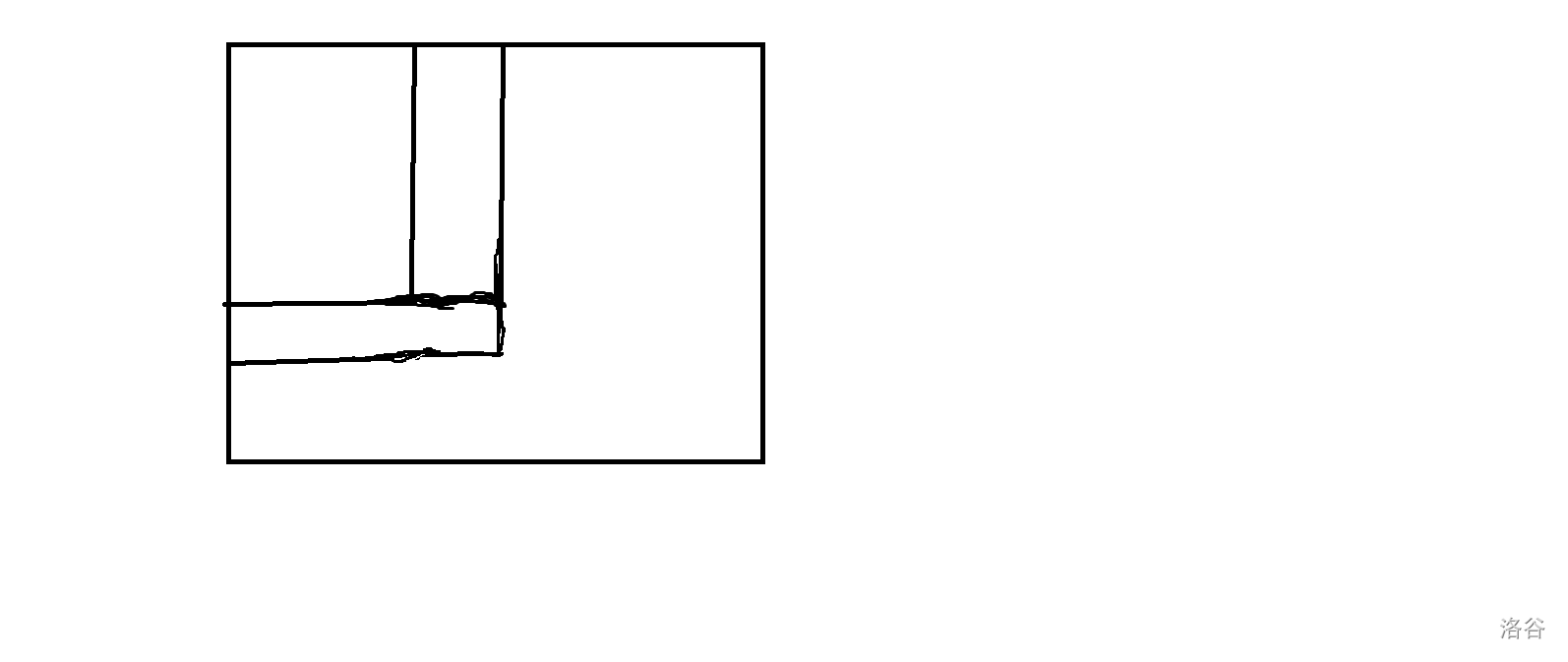
我们把这种图形称为 "L" 字形。
然后就可以考虑容斥,把所有乱涂的方案数减去包含 "L" 字形的方案数。
但是包含 "L" 字形的方案数比较难算,考虑容斥,只需算出包含至少 \(k\) 个 "L" 字形的方案数即可。
那么方案数也就是
AGC034
A - Kenken Race
显然当 \(C<D\) 时可以先把 \(B\) 移动至 \(D\),对 \(A\) 不影响。
所以只需判断 \(A,C\),\(B,D\) 之间的可达性即可。即判断两点之间是否有连续两个 #。
当 \(C>D\) 时,无论如何 \(B\) 也会影响 \(A\) ,所以找一个中转点,满足\(B\) 能到这个中转点,且这个中转点不影响 \(A\) 。
显然如果 \(B\),\(D\) 之间有 ...,那么中间那个 . 就是中转点。否则不是。
B - ABC
首先一次操作可以看做一个字符 A 往后移动了一次
那么方案数显然就是字符 A 后连续 BC 的个数。在计算连续 BC 的时候不考虑 A ,因为 A 已经被移动在所有 BC 的后面。
C - Tests
发现单调性显然,可以二分答案。那么考虑 \(\mathrm{check}(mid)\) 怎么做。
考虑把 \(mid\) 贪心地拆成 \(\lfloor \frac{mid}{X} \rfloor\) 个 \(X\) 和一个 \(mid \bmod X\)
然后把对于 \(X\) 来说贡献最佳的 \(\lfloor \frac{mid}{X} \rfloor\) 个数字填入 \(X\),并枚举填入 \(mid \bmod X\) 的位置。
D - Manhattan Max Matching
如果 \(n\) 比较小可以考虑 \(n^2\) 暴力建边跑网络流。
但是这题不行,所以考虑曼哈顿的性质,大力拆曼哈顿
点 \((x_1,y_1)\) 与点 \((x_2,y_2)\) 的曼哈顿距离为 \(|x1-x2|+|y1-y2|\),也就是 \(\max\{x_1-x_2+y_1-y_2,x_2-x_1+y_1-y_2,x_1-x_2-y_2+y_1,x_2-x_1-y_1+y_2\}\)
考虑把 \(x_1,y_1\) 与 \(x_2,y_2\) 拆开,把每种情况用一个中转点表示出来,然后大力跑费用流即可。
E - Complete Compress
考虑枚举一下根节点 \(x\),显然答案就是所有点的 \(dep\) 之和除以 \(2\)。
那么就考虑判断以这个点为根节点是否合法,即所有点是否能通过操作转移到这个点。
如果操作中的两个点满足一个点是另一个点的祖先,那么显然就是不优的。
那么把问题转为,把节点中 \(dep>0\) 的位于不同 \(x\) 子树中的两个点拉出来一一匹配,匹配后两个点的 \(dep\) 减去,那么有没有匹配方式能让这些点的 \(dep\) 最后全部归零。
然而同一个 \(u\) 子树的点也是可以匹配的。
所以考虑树形 dp,设 \(f_u\) 为 \(u\) 子树中最多能匹配 \(f_u\) 次,\(dep_u\) 为 \(u\) 子树中点距离 \(u\) 之和。
转移的时候就把最大的 \(\max\limits_{v \in son_u}\{dep_v\}\) 拿出来。
如果 \(dep_v\) 满足 \(\left(\sum_{v \in son_u} dep_v\right) \ge 2 \times dep_v\),那么显然可以全部匹配,答案为 \(\lfloor\frac{\left(\sum_{v\in son_u}dep_v\right)}{2}\rfloor\)
否则,那么匹配到最后只剩下 $2 \times dep_v-\left(\sum_{v \in son_u} dep_v\right) $ 个 \(v\) 的子树节点需要匹配,与 \(f_v\) 取 \(\min\) 即可。
最后只需判断 \(f_x\) 是否等于 \(\frac{dep_x}{2}\)
F - RNG and XOR
考虑转移式
那么就有
注意有 \(\sum_{i}p_i=1\),所以转移到最后总和是不变的。
所以 \(?=2^n-1\)
注意到有 \(p_0 \times x_i\) 贡献了每个 \(x_i\),所以有
直接 FWT 即可。
但是由于有 \(x_0=0\),所以最后每个数都要随 \(x_0\) 的值调整。
AGC033
A - Darker and Darker
多源最短路
B - LRUD Game
发现每个方向是独立的,枚举一下跳出边界的方向,模拟一下贪心过程即可。
C - Removing Coins
发现每次操作的本质就是删除所有叶子节点(直径大小减二),或者保留一个叶子节点(直径大小减一)
所以每次操作就是令直径大小减二或者减一,最后直径大小为零者败。这就是一个经典的 Bash 博弈
D - Complexity
有一个优秀的 \(\mathcal O(n^5)\) 做法。设 \(f_{l1,r1,l2,r2}\) 是以 \((l1,r1)\) 为左上角,\((l2,r2)\) 为右下角的矩阵的答案。
发现答案很小,每次只要从中间切就能令答案至多为 \(\log n+\log m\) 。
所以可以考虑换状态。设 \(f_{i,l,r,k}\) 为矩阵的上边界为 \(i\),左边界为 \(l\),右边界为 \(r\),答案为 \(k\) 时的最大下边界。
转移有两种,一种是横着转移:\(f_{f_{i,l,r,k-1},l,r,k-1}\)
另一种是竖着转移 \(\max\{\min\{f_{i,l,tmp,k-1},f_{i,tmp+1,r,k-1}\}\}\)
由于矩阵越大下边界也就越小,所以这个东西是满足单调性的。二分即可。
时间复杂度 \(\mathcal O(n^3 \log^2 n)\)
E - Go around a Circle
设 \(S\) 中的第一个字符为 R
那么圆中肯定不能有连续两个字符为 B,否则肯定至少有一个点不满足条件。
如果 \(S\)中的字符全为 R,那么除了上述限制之外圆的涂色并无限制,直接 dp 即可。
否则,我们处理出 \(S\) 中的极长连续相同字符串的长度,设为 \(R_1,B_1,R_2,B_2,\dots R_{\frac{k}{2}},B_{\frac{k}{2}}\)
注意到如果末尾极长连续相同字符串为 R 串,那么并无限制,直接消去即可,于是变成了如上情况。
对于 \(B_i\) 的限制:显然因为没有连续两个相同字符 B,所以可以通过反复横跳的形式来满足。
对于 \(A_i\) 的限制:
-
\(A_1\) 的情况。这种情况比较特殊。圆上所有连续极长
R串的长度必须是奇数而且长度不能超过 \(A_1+[2|A_1]\)。证明就考虑反证法,如果是偶数的话那么必然有一个点距离两端B的长度是都是奇数,而另一个点距离两端B的长度都是偶数,显然 \(A_1\) 无法既是偶数又是偶数,所以偶数情况不合法。而长度限制就考虑一下第一个点和第二点至少要走的步数即可。 -
\(A_{2 \sim \frac{k}{2}}\) 的情况。显然如果 \(A_i\) 是偶数可以通过反复横跳的形式来满足,所以不作考虑。而如果 \(A_i\) 是奇数的时候,每个点走过一段连续极长
R串的时候步数不能超过 \(A_i\),所以就有了长度不超过 \(A_i\) 的限制。
既然有了长度限制之后,我们考虑对于这个连续极长 R 串进行 dp。由于是个环所以还要考虑 dp 完后取分界点,直接乘上最后一段的系数即可。(顺便一提为了让方案数不重不漏,让最后一段的涂色方案为 \(1\),即为 \(RRRR\dots B\) 的情况)
由于还有一个长度为奇的限制,就直接把 \(n\) 与长度限制 \(lim\) 双双除以 \(2\),把这个限制去掉。
F - Adding Edges
以下题解是全盘借鉴 AutumnKite 的
发现如果 \(G\) 中包含边 \((a,b)\) 和 \((a,c)\),且在树 \(T\) 中有路径包含 \(a,b,c\),那么删除 \((a,c)\) 并添加 \((b,c)\) 是不影响答案的。
我们称这一操作为压缩。最后当 \(G\) 无法进行压缩操作时,\((x,y)\) 有边当且仅当在树上有路径 \(a_1,a_2,a_3,\dots,a_t\),满足 \(a_1=x,a_t=y\),且 \(\forall i,(a_i,a_{i+1}) \in G\)
那么就可以考虑压缩操作怎么做。
考虑依次加入边,设这个操作为 \(add(a,b)\),设 \(top_{a,b}\) 为 \(T\) 中距离 \(b\) 最近且在 \(G\) 中与 \(a\) 相连的点。
发现如果 \(top_{a,b}\) 存在,那么操作其实就是 \(add(a,top_{a,b})\)
否则 \(top_{a,b}=b\),连接边 \((a,b)\)
否则则考虑更新 \(b\) 子树的 \(top\)。设这个子树点为 \(v\)
-
如果 \(top_{a,v}\) 不存在,那么就令 \(top_{a,v}=b\),继续更新
-
如果 \(top_{a,v}\) 存在且 \((a,v) \in G\),由于更新是从上到下进行所以有 \(top_{a,v}=v\),那么就进行压缩操作,断开 \((a,v)\) 然后进行 \(add(b,v)\) 操作。
由于是无向图所以以上操作要做两次。最后答案也要除以 \(2\)。
ExaWizards 2019
A,B 是人口普查题,就不说了
C - Snuke the Wizard
发现每次移动操作,点的先后顺序是不变的,所以保留下来的点肯定满足原先是个区间。
二分一下区间的左端点和右端点即可。
D - Modulo Operations
题目中说明了是个 set,也就是说没有两个数字相同。发现仅有前缀最小值对答案才有贡献。那么考虑把 \(a_i\) 从大到小排序 dp,设 \(f_{i,j}\)为前 \(i\) 个数字得数为 \(j\) 的方案数,考虑转移:
-
\(a_i\) 造成贡献 \(f_{i-1,j} \rightarrow f_{i,j \mod a_i}\)
-
\(a_i\) 不造成贡献,任意排列在后面某个位置 \(f_{i-1,j} \times (n-i) \rightarrow f_{i,j}\)
E - Black or White
考虑两种情况:1.吃得只剩一种 2.吃后两种都可以选
设 \(f_i\) 为吃了第 \(i\) 块巧克力之后吃得只剩下黑巧克力的概率,\(g_i\) 为吃了第 \(i\) 块巧克力之后两种都可以选的方案数。
那么就有
答案就是 \(f_i+g_i \times \frac{1}{2^i}\)
F - More Realistic Manhattan Distance
发现如果有多条向下边的话,那么显然只有最近的一条是有用的。
向上,向左,向右边同理。
所以直接处理出离两个点最近的这些边,把交点整出来跑最短路即可。
Yahoo Programming Contest 2019
A,B,C是人口普查题就不讲了
D - Ears
发现一段路径对应的操作次数与它经过的每个点的奇偶性有关。
而路径可以看成是 一段零,一段经过偶数次,一段经过奇数次,一段经过偶数次,一段零 组成。注意中间不管哪一段都可以省略。
直接对段 dp 一下即可。
E - Odd Subrectangles
考虑枚举行,设对应行的和为奇数的列数为 \(a\),对应行的和为偶数的列数为 \(b\)。
那么方案数就是 \(2^b \times \left(\sum_{i=0}^a [i \mod 2=1]\binom {a}{i}\right)=2^b \times 2^{a-1}=2^{m-1}\)
所以每一种行的方案都对应着 \(2^{m-1}\) 种列的方案,所以考虑行的方案数是多少。
发现如果行对应的二进制数的异或和为 \(0\) 的话,那么显然无论如何选列都无法令和为奇数,否则有 \(2^{m-1}\) 种列的方案。
所以直接用线性基求出异或和为 \(0\) 的方案即可。
F - Pass
发现第 \(i+1 \sim n\) 个人的球是跑不到第 \(i\) 位上的。
所以考虑直接 dp,设 \(f_{i,j}\) 为前 \(i\) 位上有 \(j\) 个红球的方案数。
上界和下界都很显然。具体看代码。
AGC032
仅包含 \(\rm A \sim E\) 的题解。
A - Limited Insertion
读者自做不难。
B - Balanced Neighbors
发现当 \(n\) 是奇数的时候,答案就是删除 \(i+j=n\) 的边 \((i,j)\) 的完全图。
证明比较简单,每个数的相邻点之和都是 \(\frac{n(n+1)}{2}-i-j=\frac{n(n+1)}{2}-n=\frac{n(n-1)}{2}\)
但是当 \(n\) 是偶数的时候就会出错,所以答案就是删除 \(i+j=n+1\) 的边 \((i,j)\) 的完全图。
C - Three Circuits
讨论讨论一波。
-
如果有点的度数是奇数的话,显然不合法。
-
如果有点的度数大于 \(4\) 的话,那么就能以这个点为起点划分出 \(3\) 张以上的欧拉图,显然合法。
-
如果所有点的度数小于 \(4\) 的话,即所有点的度数为 \(2\) 的情况,显然就是一个环,显然不合法。
-
如果仅有一个点的度数等于 \(4\) 的话,那么显然只能划分出 \(2\) 张欧拉图,不合法。
-
如果仅有两个点的度数等于 \(4\) 的话,那么仅有下图这种情况是不合法的,特判即可。
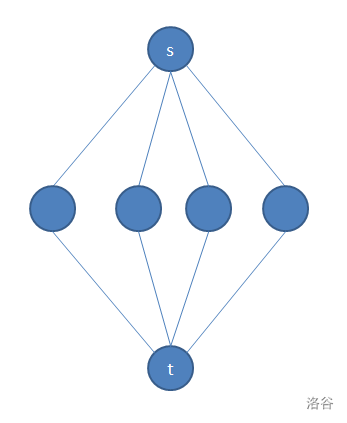
- 如果有 \(3\) 个以上的点的度数等于 \(4\) 的话,那么显然是合法的。
D - Rotation Sort
第一个操作花费为 \(A\),可以看做把一个数插入到末尾,第二个操作花费为 \(B\),可以看做把一个数插入到开头。
贪心的想,每个数字仅会被操作一次,所以考虑保留的数字,发现保留的数字肯定会是一个上升序列。
然后对这个保留的数字 dp,设 \(f_{i}\) 为令 \(a_i\) 保留,前 \(i\) 项的最小值。
就有
E - Modulo Pairing
把连接 \(x,y\) 且 \(x+y<M\) 的边看做蓝边,把连接 \(x,y\) 且 \(x+y \ge M\) 的边看做红边。
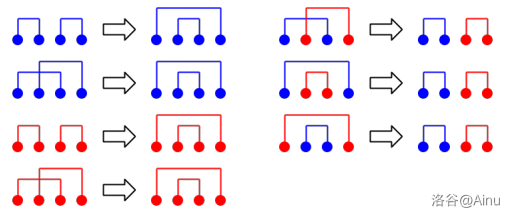
由上图可知,最优连边方式一定如下图:

二分出这个分界点即可。
AGC031
仅包含 \(\rm A\sim E\) 的题解。
A - Colorful Subsequence
读者自做不难。
B - Reversi
考虑 dp,设 \(f_i\) 为 \(1 \sim i\) 的方案数。则有:
C - Differ by 1 Bit
把所有值异或 \(A\),于是问题就变成构造 \(P_0=0,P_{2^n-1}=A \oplus B\) 。
显然 \(\rm popcount(A \oplus B)\) 是偶数的话,那么是无解的。因为有 \(2^n-1\) 次改变位数,而 \(2^n-1\) 显然是奇数,与 \(\rm popcount(A \oplus B)\) 是偶数的情况相冲突,所以无解。
考虑分治 \((l,r)\),把 \([l,mid]\) 中 \(p_{2^n-1}\) 为 \(1\) 的某一位设为 \(0\),把 \([mid+1,r]\) 中 \(p_{2^n-1}\) 为 \(1\) 的某一位 设为 \(1\),然后中转点在满足有奇数个位不同的情况下随便枚举即可。
具体见代码
D - A Sequence of Permutations
有 \(a_1=p,a_2=q,a_3=f(p,q)\)
有
所以就有 \(f(p,q)=p^{-1}q\)
于是就有
设 \(x=q^{-1}pqp^{-1}\),则有 \(a_n=ra_{n-6}r^{-1}\)
然后直接置换快速幂即可。
E - Snuke the Phantom Thief
考虑一维的时候怎么做。
枚举一下盗窃数量 \(k\),把盗窃物品按坐标排序,然后两个限制分开考虑:
- 坐标小于等于 \(a_i\) 的最多偷 \(b_i\) 个
也就是说要让 \(b_i+1 \sim k\) 的盗窃物品坐标必须大于 \(a_i\)
- 坐标大于等于 \(a_i\) 的最多偷 \(b_i\) 个
也就是说要让 \(1 \sim n-b_i\) 的盗窃物品坐标必须大于 \(a_i\)。
然后就可以考虑建图,\(k\) 个点代表按坐标排序的盗窃物品,\(n\) 个点代表待盗窃的物品,直接建二分图即可。
二维的情况大体同上,具体见代码
ARC106
被帅哥 zyk 带飞了 /se/qq
A,B 是签到题
C - Solutions
考场上想到正解,然而一直在弱智地想 \(M<0,M \ge N-1\) 时怎么做...
发现这种情况能构造 \(M \ge 0\) 时的解。
然后读者自做不难。
D - Powers
转化成求 \(\sum_{i=1}^n\sum_{j=1}^n(a_i+a_j)^X\)
推一波式子
发现后面这个卷积一下就行。
时间复杂度 \(\mathcal{O}(nK+K^2)\)
E - Medals
不会
F - Figures
考虑 prufer 序列。
设最后所有点的度数为 \(d_1,d_2,\cdots,d_n\),每个点度数的限制为 \(D_1,D_2,\cdots,D_n\)
答案就是
推一波式子
发现后面这个就是范德蒙德卷积,于是答案即为
ARC108
日常被帅哥 zyk 带飞,已经习惯了(((
A,B,C都是憨憨题
D - AB
菜鸡来翻译官方题解了
分类讨论,设 \(c_{AB}=\) B,\(c_{AB}=\) A 时同理。
如果 \(c_{BB}=\) B 的话,那么显然只能插入 B 字符,答案为 \(1\)。否则 \(c_{BB}\)= A,继续讨论。
手玩一下,发现 \(n=3\) 时只有 ABB 一个串可以生成,\(n=4\) 时有 ABAB,ABBB 两个串可以生成,\(c_{AB},c_{BB}\) 已经讨论过了,所以接下去需要讨论 \(c_{BA}\)
如果 \(c_{BA}=\) A,那么生成的字符串除了第一个字符是 A,末尾两个字符是 AB 外,其他字符可以任意生成,答案是 \(2^{n-3}\)
否则,\(c_{BA}=\) B,最后生成的串显然一定不含有子串 AA,满足这个条件的所有串都是可以生成的,则对中间的这个串(即生成的串去掉第一个字符 A和最后两个字符 AB 后的串)进行 dp,设 \(f_i\) 为中间的串长度为 \(i\) 时的方案数。
由于这个中间的串要和第一个字符 A 进行拼接,所以中间的串的第一个字符肯定不是 A,否则会形成子串 AA。所以我们枚举中间串的第一个字符和第二个字符来 dp。
-
第一个字符是
B,第二个字符是B,方案数是 \(f_{i-1}\) -
第一个字符是
B,第二个字符是A,方案数是 \(f_{i-2}\)
所以 \(f_{i}=f_{i-1}+f_{i-2}\),也就是斐波那契数列的递推公式。
时间复杂度 \(\mathcal{O}(\log n)\),开 n=1000 完全是唬人的
E - Random IS
发现一个东西被标记之后,剩下来的操作次数可以通过递归这个东西的左侧区间和右侧区间来统计,于是考虑区间 dp。
设 \(f_{l,r}\) 为 \(l\) 物品,\(r\) 物品均被标记时的期望操作次数。
设 \(t_{l,r}=\sum_{i=l+1}^{r-1}[a_l<a_i<a_r]\)
那么有
可以把 \(f_{l,i}\) 与 \(f_{i,r}\) 的贡献拆开来,用数据结构优化即可。
时间复杂度 \(\mathcal{O}(n^2\log n)\)
F - Paint Tree
统计答案只需枚举 \(\max(X,Y)\) 的值 \(i\),然后考虑当 \(\max(X,Y)=v\) 时有多少种方案。
根据直径的性质,相同颜色的最远路径之一的端点之一必然是直径的端点之一。
所以我们只需要考虑两个直径端点 \(s,t\) 以及每个点和这两个端点的距离。
如果 \(s,t\) 染成同一个颜色的话,那么显然就有贡献 \(\mathrm{dist(s,t) \times 2^{n-1}}\),然后考虑 \(s,t\) 染成不同颜色的情况。设 \(s\) 为白色,\(t\) 为黑色。
我们增加一个定义为 特殊颜色,当 \(\mathrm{min(dist(i,s),dist(i,t))=dist(i,s)}\) 时,\(i\) 的优秀颜色就是白色,否则就是黑色。
显然 \(\max(X,Y)\) 至少有 \(\max\limits_{i\not = s,i\not =t}\{\min(\mathrm{dist(i,s),dist(i,t)})\}\),当 \(v\) 小于这个值的时候方案数为 \(0\)。
否则:
-
对于 \(\max(\mathrm{dist(i,s),dist(i,t)})>v\) 的点,显然这些点只能染成对应的特殊颜色。
-
对于 \(\max(\mathrm{dist(i,s),dist(i,t)})=v\) 的点,显然这些点可以任意染色,但是不能所有点都染成它们对应的特殊颜色。
-
对于 \(\max(\mathrm{dist(i,s),dist(i,t)})<v\) 的点,显然这些点可以任意染色。
直接对可以任意染色的点取一下前缀和即可。



