CART回归树基本原理(具体例子)
id3不能直接处理连续性的特征,需要将连续性的转化成离散的,但是会破坏连续性特征的内在结构。
一、概念
CART全称叫Classification and Regression Tree。首先要强调的是CART假设决策树是二叉树,内部结点特征的取值只有“是”和“否”,左分支是取值为“是”的分支,有分支则相反。这样的决策树等价于递归地二分每个特征。
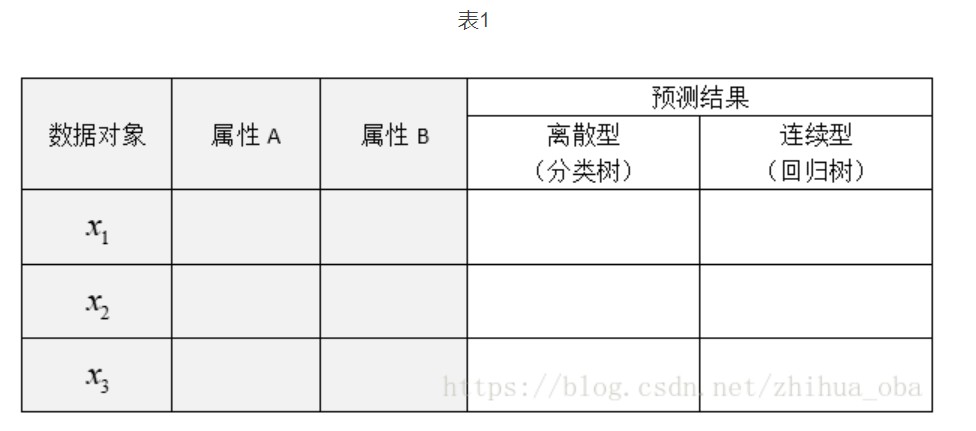
CART分类回归树是一种典型的二叉决策树,可以做分类或者回归。如果待预测结果是离散型数据,则CART生成分类决策树;如果待预测结果是连续型数据,则CART生成回归决策树。数据对象的属性特征为离散型或连续型,并不是区别分类树与回归树的标准,例如表1中,数据对象的属性A、B为离散型或连续型,并是不区别分类树与回归树的标准。作为分类决策树时,待预测样本落至某一叶子节点,则输出该叶子节点中所有样本所属类别最多的那一类(即叶子节点中的样本可能不是属于同一个类别,则多数为主);作为回归决策树时,待预测样本落至某一叶子节点,则输出该叶子节点中所有样本的均值。
二、CART生成
决策树的生成就是递归地构建二叉决策树的过程,对回归树用平方误差最小化准则,对分类树用基尼指数最小化准则,进行特征选择,生成二叉树。
三、回归树的生成最小二叉回归树生成算法:
1、选择最优切分变量j与切分点s,求解:
遍历变量j,对固定的切分变量j扫描切分点s,选择使上式取得最小值的对(j,s)。其中Rm是被划分的输入空间,Cm空间Rm对应的输出值。
3、继续对两个子区域调用步骤1,直至满足停止条件。
4、将输入空间划分为M个区域R1,R2,...Rm生成决策树:
四、示例
上面的东西有点难以理解,下面举个例子来说明。
训练数据见下表,x的取值范围为区间[0.5,10.5],y的取值范围为区间[5.0,10.0],学习这个回归问题的最小二叉回归树。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 5.56 | 5.70 | 5.91 | 6.40 | 6.80 | 7.05 | 8.90 | 8.70 | 9.00 | 9.05 |
求解训练数据的切分点s:
容易求得在R1、R2内部使得平方损失误差达到最小值的c1、c2为:
这里N1、N2是R1、R2的样本点数。
求训练数据的切分点,根据所给数据,考虑如下切分点:
1.5,2.5,3.5,4.5,5.5,6.5,7.5,8.5,9.5。
对各切分点,不难求出相应的R1、R2、c1、c2及
例如,当s=1.5时,R1={1},R2={2,3,...,10},c1=5.56,c2=7.50,则
现将s及m(s)的计算结果列表如下:
| s | 1.5 | 2.5 | 3.5 | 4.5 | 5.5 | 6.5 | 7.5 | 8.5 | 9.5 |
|---|---|---|---|---|---|---|---|---|---|
| m(s) | 15.72 | 12.07 | 8.36 | 5.78 | 3.91 | 1.93 | 8.01 | 11.73 | 15.74 |
由上表可知,当x=6.5的时候达到最小值,此时R1={1,2,...,6},R2={7,8,9,10},c1=6.24,c2=8.9,所以回归树T1(x)为:
posted on 2020-03-05 18:58 limingqi 阅读(13977) 评论(1) 编辑 收藏 举报

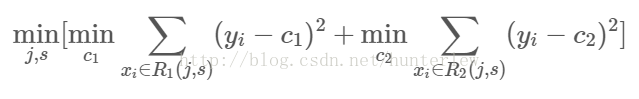
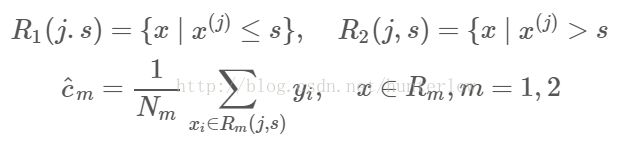
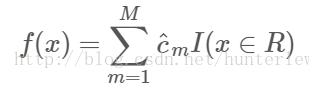
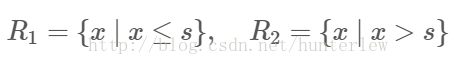
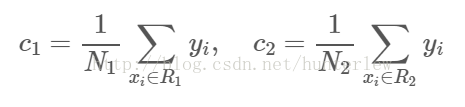
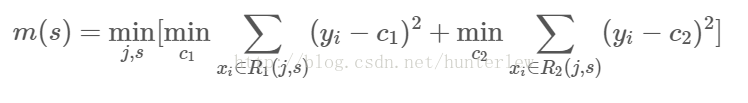

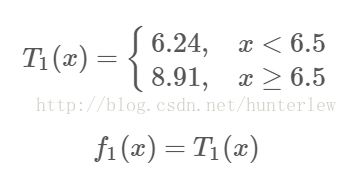



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 地球OL攻略 —— 某应届生求职总结
· 提示词工程——AI应用必不可少的技术
· Open-Sora 2.0 重磅开源!
· 周边上新:园子的第一款马克杯温暖上架