方向导数及梯度
z = f(x,y) x,y属于集合D,M0(x0,y0)属于集合D
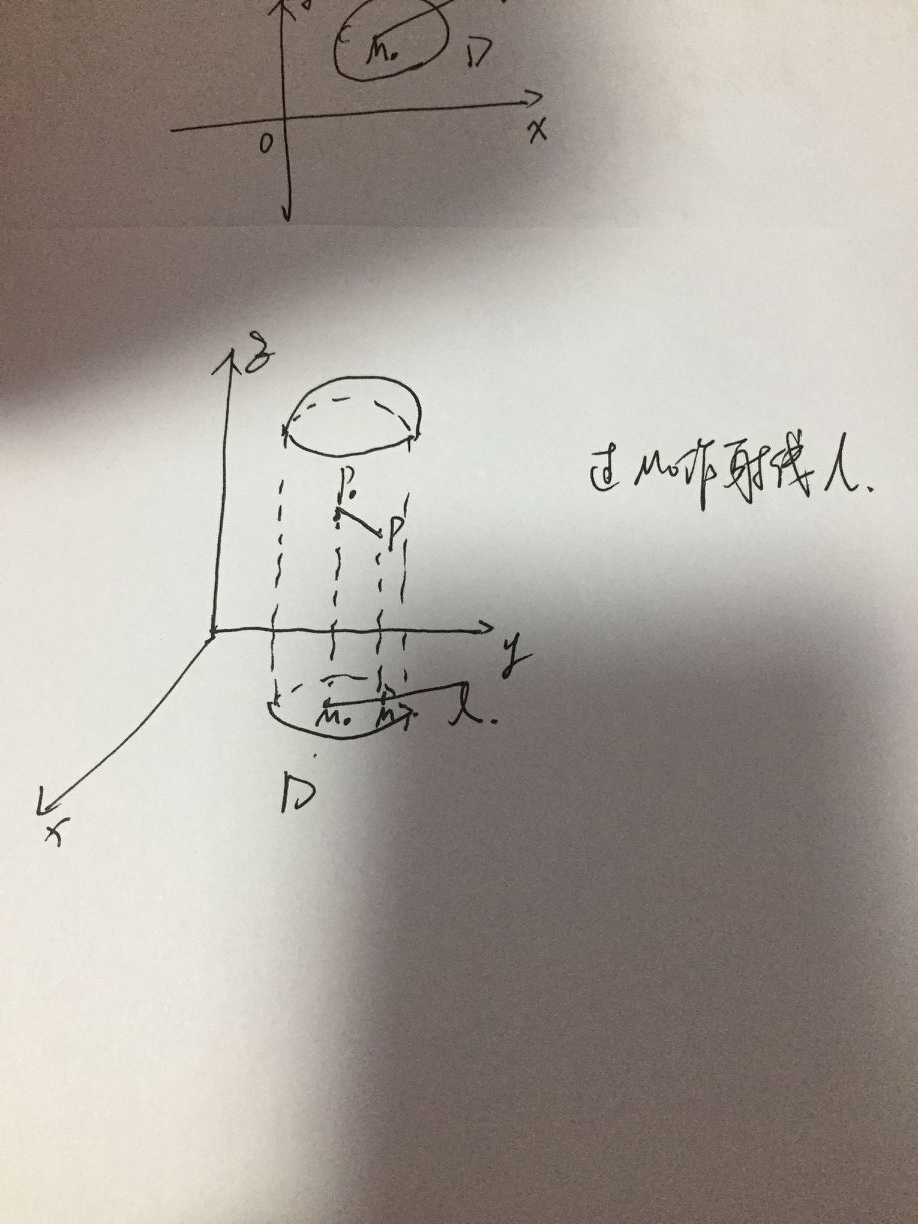
见图可知,可以类比于上山下山的过程,在M0点是此时在p0点的一个向下的投影,在p0点存在上山下山情况,可以去各个方向。过m0点做一条射线l,上面存在m点(x0+Δx,y0+Δy)在l上在l上,Δz = f(x0+Δx,y0+Δy)-f(x0,y0) , m0到m的距离为k=√Δx^2+Δy^2 , k→0时 if 极限存在 lim ΔZ /k 此极限为z=f(x,y)在m0点沿射线l的方向导数,∂z/∂l 在m0点的方向导数。在其他空间上诉仍然成立,
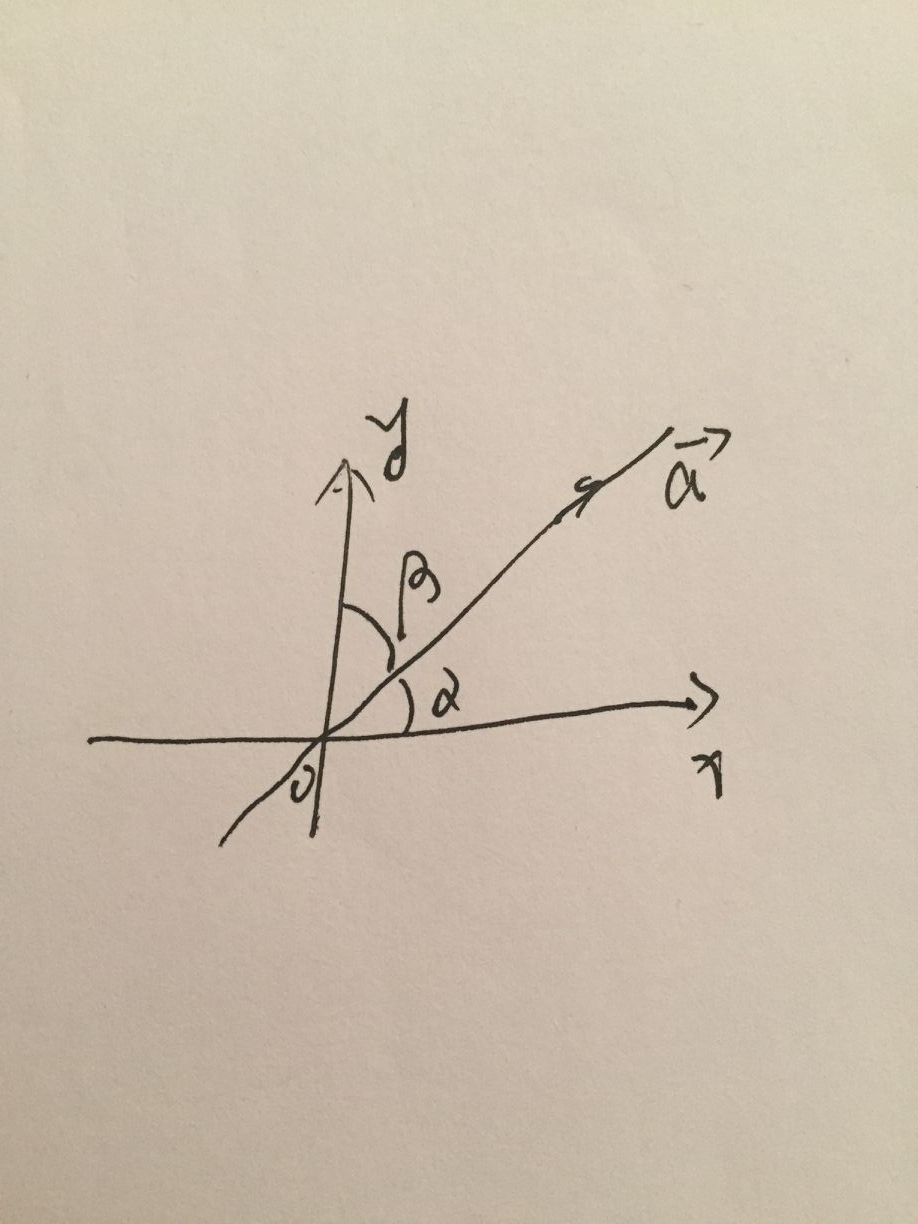
(cosα ,cosβ) 为方向角是在向量a(x,y)方向上的单位向量,cosα=x/|a|,cosβ=y/|a| ,方向余弦,方向导数为∂z/∂x *cosα + ∂z/∂y *cosβ=(∂z/∂x,∂z/∂y)*(cosα,cosβ),前面固定的向量为数值在m0点,后面的是在l方向上的单位向量,利用向量公式展开 a*b=|a|*|b|*cosθ ,因为前面展开是常数,所以只是和cosθ 有关,当θ=0时,cosθ去最大为1,因此(∂z/∂x,∂z/∂y)为在该点的梯度,梯度方向是方向导数最大的方向,上升降低最快的方向。

本文来自博客园,作者:limingqi,转载请注明原文链接:https://www.cnblogs.com/limingqi/p/11604346.html

 浙公网安备 33010602011771号
浙公网安备 33010602011771号