opencv-PCA主要成分分析
资料：https://www.cnblogs.com/xyf327/p/14824106.html
OpenCV3.3中给出了主成分分析(Principal Components Analysis, PCA)的实现，即cv::PCA类
PCA在opencv项目中的应用：
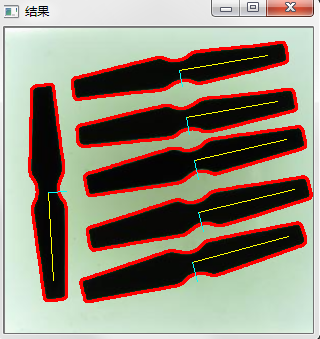
- 获取物体主要方向（形心）
- 对数据集降维处理
(1)、cv::PCA::PCA：构造函数；
(2)、cv::PCA::operator()：函数调用运算符；
(3)、cv::PCA::project：将输入数据投影到PCA主成分空间；
(4)、cv::PCA::backProject：重建原始数据；
(5)、cv::PCA::write：将特征值、特征向量、均值写入指定的文件；
(6)、cv::PCA::read：从指定文件读入特征值、特征向量、均值；
(7)、cv::PCA::eigenvectors：协方差矩阵的特征向量；
(8)、cv::PCA::eigenvalues：协方差矩阵的特征值；
(9)、cv::PCA::mean：均值
特征向量 特征值
4.png
#include<opencv2/opencv.hpp> #include<iostream> #include <vector> int main(int argc, char** argv) { double getOrientation(std::vector<cv::Point> &pts, cv::Mat & img); cv::Mat src = cv::imread("D:/bb/tu1/4.png"); cv::Mat gray, binary; cv::cvtColor(src, gray, cv::COLOR_BGR2GRAY); cv::threshold(gray, binary, 150, 255, cv::THRESH_BINARY);//阈值处理 std::vector<std::vector<cv::Point> > contours; std::vector<cv::Vec4i> hierarchy; findContours(binary, contours, hierarchy, cv::RETR_LIST, cv::CHAIN_APPROX_NONE);//寻找轮廓坐标 for (int i = 0; i < contours.size(); ++i) { double area = contourArea(contours[i]); if (area < 1e2 || 1e4 < area) continue;//去除过小或者过大的轮廓区域（科学计数法表示le2表示1X10的2次方） cv::drawContours(src, contours, i, cv::Scalar(0, 0, 255), 2, 8, hierarchy, 0);//画出轮廓 double angle = getOrientation(contours[i], src); std::cout << angle << std::endl; } cv::imshow("结果", src); cv::waitKey(0); return 0; } double getOrientation(std::vector<cv::Point>& pts, cv::Mat& img) { cv::Mat data_pts = cv::Mat(pts.size(), 2, CV_64FC1);//使用mat来保存指定轮廓坐标点数据，也是为了后面pca处理需要 //创建contours[i].size()行2列的矩阵;contours[i].size()是轮廓的坐标点数 //OpenCV的PCA输入必须要是单信道32位浮点数格式或是单信道64位浮点数格式的,参数为CV_32FC1或是CV_64FC1 for (int i = 0; i < data_pts.rows; ++i) { data_pts.at<double>(i, 0) = pts[i].x; data_pts.at<double>(i, 1) = pts[i].y; } cv::PCA pca_analysis(data_pts, cv::Mat(), 0);//执行PCA分析 //参数具体含义，看下面的实例 cv::Point pos = cv::Point(pca_analysis.mean.at<double>(0, 0), pca_analysis.mean.at<double>(0, 1)); //获得最主要分量(均值)，在本例中，对应的就是轮廓中点，也是图像中点 //pca_analysis.mean.at<double>(0, 0) 返回轮廓中心(均值)x坐标 //pca_analysis.mean.at<double>(0, 1) 返回轮廓中心(均值)y坐标 //cv::circle(img, pos, 3, cv::Scalar(0, 0, 255), -1);//画出轮廓中心 std::vector<cv::Point2d> eigen_vecs(2);//保存轮廓特征向量的两个点 std::vector<double> eigen_val(2); //保存特征值--每个轮廓有两个 for (int j = 0; j < 2; ++j) { eigen_vecs[j] = cv::Point2d(pca_analysis.eigenvectors.at<double>(j, 0), pca_analysis.eigenvectors.at<double>(j, 1)); //pca_analysis.eigenvectors.at<double>(j, 0) 返回轮廓协方差矩阵的特征向量x //pca_analysis.eigenvectors.at<double>(j, 1) 返回轮廓协方差矩阵的特征向量y //每个轮廓的特征向量包含两个点：参数1：j表示第几个点；参数2：表示x或y //特征向量值在(-1,1) eigen_val[j] = pca_analysis.eigenvalues.at<double>(j, 0);//返回特征值 //参数1：0表示x方向的特征值；1表示y方向的特征值 cv::line(img, pos, pos + 0.02 * cv::Point(eigen_vecs[0].x * eigen_val[0], eigen_vecs[0].y * eigen_val[0]), CV_RGB(255, 255, 0)); //计算出直线，在主要方向上绘制直线（每个特征向量乘以其特征值并转换为平均位置。有一个 0.02 的缩放系数，它只是为了确保矢量适合图像并且没有 10000 像素的长度） cv::line(img, pos, pos + 0.1 * cv::Point(eigen_vecs[1].x * eigen_val[1], eigen_vecs[1].y * eigen_val[1]), CV_RGB(0, 255, 255)); } return std::atan2(eigen_vecs[0].y, eigen_vecs[0].x);//最终计算并返回一个最强的(即具有最大特征值）的特征向量的角度 }
对数据集降维处理
对一副宽p、高q的二维灰度图，要完整表示该图像，需要m = p*q维的向量空间,比如100*100的灰度图像，它的向量空间为100*100=10000。下图是一个3*3的灰度图和表示它的向量表示：
该向量为行向量，共9维，用变量表示就是[v0, v1, v2, v3, v4, v5, v6, v7, v8]，其中v0...v8，的范围都是0-255。
现在的问题是假如我们用1*10000向量，表示100*100的灰度图，是否向量中的10000维对我们同样重要？肯定不是这样的，有些维的值可能对图像更有用，有些维相对来说作用小些。为了节省存储空间，我们需要对10000维的数据进行降维操作，这时就用到了PCA算法，该s算法主要就是用来处理降维的，降维后会尽量保留更有意义的维数，它的思想就是对于高维的数据集来说，一部分维数表示大部分有意义的数据
#include<opencv2/opencv.hpp> #include<iostream> #include <vector> //把图像归一化为0-255，便于显示 cv::Mat norm_0_255(const cv::Mat& src) { cv::Mat dst; switch (src.channels()) { case 1: cv::normalize(src, dst, 0, 255, cv::NORM_MINMAX, CV_8UC1); break; case 3: cv::normalize(src, dst, 0, 255, cv::NORM_MINMAX, CV_8UC3); break; default: src.copyTo(dst); break; } return dst; } //转化给定的图像为行矩阵 cv::Mat asRowMatrix(std::vector<cv::Mat>& src, int rtype, double alpha = 1, double beta = 0) { /* 参数1:需要转换的矩阵集合 参数2:转换后的矩阵数据类型 */ size_t n = src.size(); //矩阵数量 if (n == 0)return cv::Mat();//如果没有矩阵，返回空矩阵 size_t d = src[0].total();//矩阵中的像素总数 cv::Mat data(n, d, rtype); for (int i = 0; i < n; i++) { //拷贝数据 cv::Mat xi = data.row(i); if (src[i].isContinuous()) { //如果是连续矩阵 src[i].reshape(1, 1).convertTo(xi, rtype, alpha, beta); //修改成1通道1行矩阵并转换数据类型后保存到xi矩阵 } else { //非连续矩阵 src[i].clone().reshape(1, 1).convertTo(xi, rtype, alpha, beta); } } return data; } int main(int argc, char** argv) { std::vector<cv::Mat> db; //读入10个人脸图像，这些图像大小相等，是一个人的各种表情图片 //10个人脸下载:链接：https://pan.baidu.com/s/1CPOebkpwGAvHvE24-SGvCQ 提取码：6666 db.push_back(cv::imread("D:/bb/lian/1.png", 0)); //96X116图像:116行X96列=11136 db.push_back(cv::imread("D:/bb/lian/2.png", 0)); db.push_back(cv::imread("D:/bb/lian/3.png", 0)); db.push_back(cv::imread("D:/bb/lian/4.png", 0)); db.push_back(cv::imread("D:/bb/lian/5.png", 0)); db.push_back(cv::imread("D:/bb/lian/6.png", 0)); db.push_back(cv::imread("D:/bb/lian/7.png", 0)); db.push_back(cv::imread("D:/bb/lian/8.png", 0)); db.push_back(cv::imread("D:/bb/lian/9.png", 0)); db.push_back(cv::imread("D:/bb/lian/10.png", 0)); cv::Mat data = asRowMatrix(db, CV_32FC1); //执行之后，data是10行矩阵，每行是一个图片 int num_components = 5; // PCA算法保持5主成分分量---降维处理 cv::PCA pca(data, cv::Mat(), 0, num_components);//执行pca算法 //参数1:为要进行PCA变换的输入Mat //参数2:为该Mat的均值向量 //参数3:为输入矩阵数据的存储方式，如果其值为CV_PCA_DATA_AS_ROW=0则说明输入Mat的每一行代表一个样本，同理当其值为CV_PCA_DATA_AS_COL=1时，代表输入矩阵的每一列为一个样本 //参数4:该PCA计算时保留的最大主成分的个数。如果是缺省值，则表示所有的成分都保留 cv::Mat mean = pca.mean.clone(); //均值矩阵 std::cerr << "mean行数=" << mean.rows << ", " << "mean列数=" << mean.cols << std::endl; //行数=1，列数=11136 cv::Mat eigenvalues = pca.eigenvalues.clone();//特征值矩阵 cv::Mat eigenvectors = pca.eigenvectors.clone();//特征向量矩阵 mean=mean.reshape(1, db[0].rows); mean = norm_0_255(mean); cv::namedWindow("均值脸",0); cv::imshow("均值脸", mean); //五个特征脸 std::cerr << "eigenvectors行数=" << eigenvectors.rows << ", " << "eigenvectors列数=" << eigenvectors.cols << std::endl; //行数=5，列数=11136;这个行数由PCA的参数4决定，也就是最大主成分的个数 cv::Mat row0 = pca.eigenvectors.row(0).clone();//获取第一个特征脸的数据 row0 = row0.reshape(1, db[0].rows); row0 = norm_0_255(row0); cv::namedWindow("第1特征脸", 0); cv::imshow("第1特征脸", row0); cv::Mat row1 = pca.eigenvectors.row(1).clone();//获取第2个特征脸的数据 row1 = row1.reshape(1, db[0].rows); row1 = norm_0_255(row1); cv::namedWindow("第2特征脸", 0); cv::imshow("第2特征脸", row1); cv::Mat row2 = pca.eigenvectors.row(2).clone();//获取第3个特征脸的数据 row2 = row2.reshape(1, db[0].rows); row2 = norm_0_255(row2); cv::namedWindow("第3特征脸", 0); cv::imshow("第3特征脸", row2); cv::Mat row3 = pca.eigenvectors.row(3).clone();//获取第4个特征脸的数据 row3 = row3.reshape(1, db[0].rows); row3 = norm_0_255(row3); cv::namedWindow("第4特征脸", 0); cv::imshow("第4特征脸", row3); cv::Mat row4 = pca.eigenvectors.row(4).clone();//获取第5个特征脸的数据 row4 = row4.reshape(1, db[0].rows); row4 = norm_0_255(row4); cv::namedWindow("第5特征脸", 0); cv::imshow("第5特征脸", row4); cv::waitKey(0); return 0; }
