Codeforces 1339D - Edge Weight Assignment （数据结构 - 树）

Description

思路

这题总觉得有些想法，但是就是写不出来。看了题解好久才想明白。(以下均图片来自cf题解)

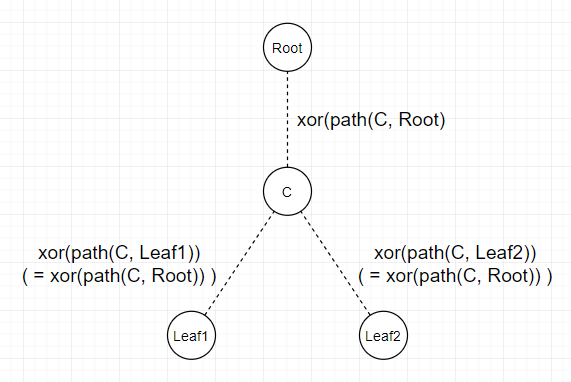
每个度数大于2的结点都是某些叶子结点的LCA，设这个结点为图中的C。虚线代表从叶子结点到C的路径，把路径上面的边全部合并，看成一条边。合并的边的权值就是路径上的边的权值的异或。

对树进行这样的处理之后，一个点要么是叶子结点，要么是LCA点（设为C点）。如果是C点，那它要么连接叶子结点，要么连接另一个C点。
根据题意，xor(path(leaf1, C)) == xor(path(leaf2, C)) == xor(path(root, C))
由于C点可能连接多个叶子结点，显然，所有path(leaf, C)权重都要相等，因此把这些叶子结点都合并为一个(即可以把leaf1，leaf2, 合成一个结点)。

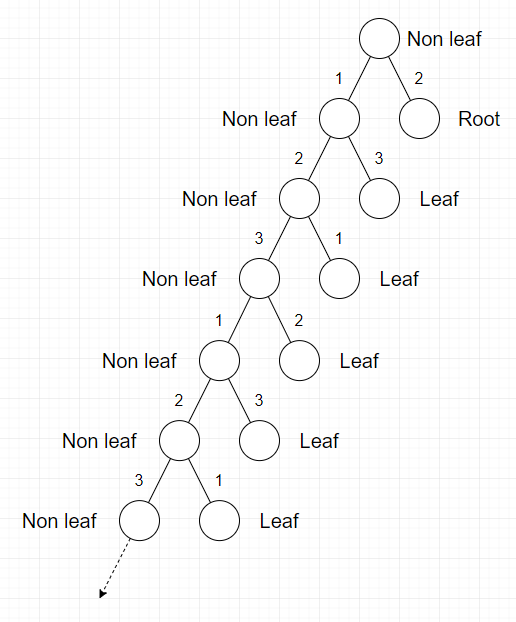
这样，任何的树都可以转化为下面这些图这种形式。
分情况讨论

1. 对于最小的f，总是可以用不多于3个数字。如果每个叶子点对之间的距离都是偶数（即所有叶子点奇偶性都是偶数），那么最小f为1，否则为3。
   

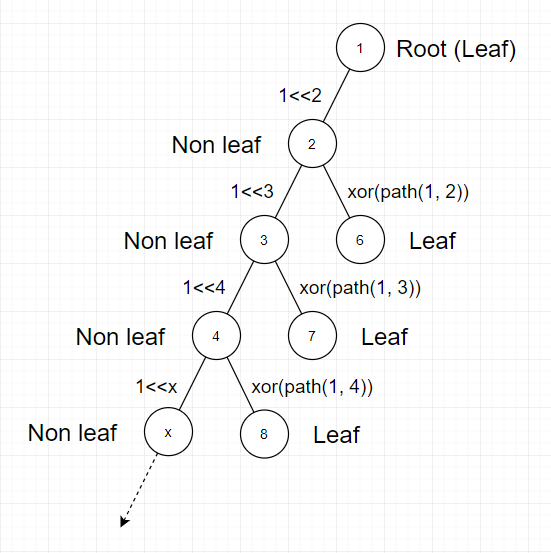
2. 对于最大的f，见图和cf题解很容易知道成立。最大的f为所有边的个数减去（每个C点连接的叶子点个数(未合并前) - 1）
   

#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef long long ll;
const int N = 1e5 + 10;
 
vector<int> np[N];
int cnt[N];
int p[N];
 
void dfs(int u, int fa, int par) {
    p[u] = par;
    for(auto v : np[u]) {
        if(v == fa) continue;
        dfs(v, u, par ^ 1);
    }
}
 
int main() {
    ios::sync_with_stdio(false);
    int n;
    cin >> n;
    for(int i = 0; i < n - 1; i++) {
        int u, v;
        cin >> u >> v;
        np[u].push_back(v);
        np[v].push_back(u);
        cnt[u]++;
        cnt[v]++;
    }
    
    int mn = 1, mx = n - 1;
    for(int i = 1; i <= n; i++) {
        if(cnt[i] == 1) {
            dfs(i, -1, 0);
            break;
        }
    }
    
    for(int i = 1; i <= n; i++) {
        if(cnt[i] == 1 && p[i] == 1) {
            mn = 3;
            break;
        } 
    }
    
    for(int i = 1; i <= n; i++) {
        int ch = 0;
        for(auto v : np[i]) {
            if(cnt[v] == 1) {
                ch++;
            }
        }  
        if(ch != 0)
            mx -= (ch - 1);
    }
    
    cout << mn << " " << mx << endl;
}