DS博客作业05--查找

0.PTA得分截图

1.本周学习总结

1.1 总结查找内容🎃

💌楔子
查找表：同一类型的数据元素构成的集合，其数据元素之间具有松散的关系
查找：给定一个值，在查找表中查找关键字与这个值对应的数据元素

  • 关键字：用来表示数据元素的某一个数据项的值
  • 主关键字：可以唯一识别一个数据元素的关键字
  • 此关键字：可以识别若干个数据元素的关键字

💎查找的性能指标ASL

  • ASL:关键字的平均比较次数，也称平均搜索长度

    • 公式:
      • n:记录的个数,即数据元素的个数
      • pi:查找第i个记录的概率 通常认为:pi=1/n
      • ci:找到第i个记录时,比较的次数
        每种查找的ASL指标算法都不一样，这是大致的公式

  • 以下展开说：

💟顺序查找

  • 如果每个关键字查找概率相同，则查找成功时 ASL=(n+1)/2。（通过公式和以第一项为1 公差为1的前n项和得出）
    • 一般都是概率相同。由以上结论的出：查找成功时的平均比较次数约为表长的一半。
  • 查找不成功时
    • 一般查找不成功的时候，都是已经找完整个表都还没找到，所以跟表的长度有关 即 n
    • 查找不成功时的ASL=n
  • 顺序查找算法
int SeqSearch(SeqList R,int n,KeyType k)
{
    int i=0;
    while (i<n && R[i].key!=k)	//从表头往后找
	i++;
    if (i>=n)			//未找到返回0
	return 0;
    else 
	return i+1;//找到返回逻辑序号i+1
}

💟二分查找

二分查找也是称为折半查找，就是不断的缩小区域一半一半的缩小，比如：如果中间值比关键字小就更改最大的值为中间值，不断更新中间值，直到最大的值与中间值相等时
-ASL：

  • 二分查找的ASL文字不好说明，所以💮举个栗子
    • 二分查找判定树，建成一棵树来进行计算。每次把中间值作为根，然后左边（小）区域的中间值做根为左孩子，右边（大）区域中间值做根为右孩子，以此类推
      • 当n比较大时，判定树看成内部节点的总数为n=2h-1、高度为h=log2(n+1)的满二叉树
  • 二分查找算法（递归）
int BinSearch1(SeqList R,int low,int high,KeyType k)
{
   int mid;
   if (low<=high)		　//查找区间存在一个及以上元素
   {
       mid=(low+high)/2;  //求中间位置
       if (R[mid].key==k) //查找成功返回其逻辑序号mid+1
	     return mid+1;
       if (R[mid].key>k)  //在R[low..mid-1]中递归查找
	     BinSearch1(R,low,mid-1,k);
       else		//在R[mid+1..high]中递归查找
	     BinSearch1(R,mid+1,high,k);
   }
   else
       return 0;
}

💎动态查找
💟二叉搜索树
二叉搜索树也叫二叉排序树，这个数的性质跟二分判定树很像

  • 特点

    • 空树也是一颗二叉搜索树
    • 若存在根节点，且左子树不空，则左子树上的所有节点均小于根节点
    • 若存在根节点，且右子树不空，则右子树上所有的节点均大于根节点
    • 一个二叉搜索树其左右子树也一定是一颗二叉搜索树
    • 其中序遍历得到的序列是一个递增序列
      拿上面的💮栗子来说：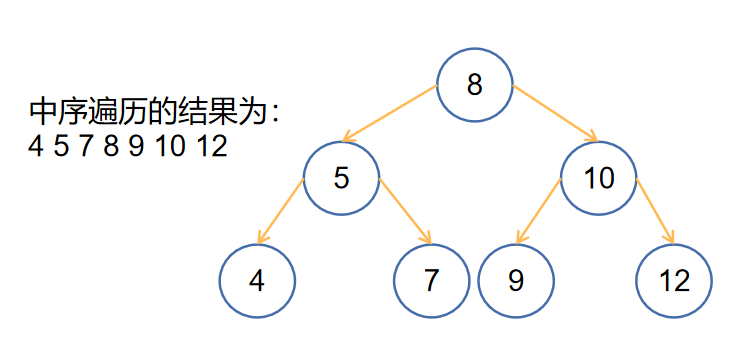

  • 数据类型定义

typedef struct node 
{
       KeyType key;            	  //关键字项
　     InfoType data;          	  //其他数据域
       struct node *lchild，*rchild; 	  //左右孩子指针
}BSTNode,*BSTree;

💡二叉搜索树的查找

  • 其类似于二分查找，文字说明就是，如果数为空或者已找到都返回bt，如果要查找的关键字小于树的关键字 则递归左子树，如果要查找的关键字大于树的关键字则递归右子树
  • 其代码如下
BSTNode *SearchBST(BSTNode *bt,KeyType k)
 { 
    if (bt==NULL || bt->key==k)   
       return bt;
    if (k<bt->key)   return SearchBST(bt->lchild,k);
    else  return SearchBST(bt->rchild,k);
 }

💡二叉搜索树的构建即插入

  • 已经了解了二叉搜索树的查找，那么二叉树的构建即插入可以用一句话来概括：边查找边插入
    🌞以下配合代码讲解
      • 首先需要判断是否为空树，为空树则为头结点分配储存空间，是红色标出来的那一段代码，而绿色标出来的代码则是判断二叉树中是否已经有了这个数据，有就退出并且返回0，
      • 剩下蓝色的代码则是判断关键字k对比当前节点值的大小，若是小于则去往左子树递归插入，若是大于则去往右子树递归插入。
        ❣需要注意的是，二叉排序树插入的时候都是插入到树的一条路径的末尾上，所以当遍历到空节点的时候，就可以为该节点分配空间，插入到二叉树当中了，这也是！红色代码！的用处

💡二叉搜索树的删除

  • 二叉树的删除要考虑的东西比较多，文字说明比较白 这里也是打算配合代码来讲
    🌞以下配合代码讲解
    • 删除节点分为三种情况
      • 要删除的节点左孩子为空，❣红色代码
        左孩子为空的情况，当左孩子为空，我们可以用将右孩子的节点代替被删除节点，也就是将右孩子的数值给了被删除节点，然后将被删除节点删除
      • 要删除的节点右孩子为空，❣蓝色代码
        被删除节点右孩子节点为空的情况也类似第一种，将左孩子节点代替被删除节点，然后将被删除节点删除即可
      • 左右孩子都不为空，❣黑色代码
        这种情况的时候，由二叉搜索树的特点可知，中序遍历的话会是一个递增序列
  • 此时提出一个问题：我们要用哪一个节点来代替这个要被删除的节点呢？
    🕵️‍♂️很简单就是数值排在被删除节点前面的这个节点，我们也会叫它前驱节点，这个在之前线索二叉树的遍历有讲到过，遍历的时候在某个节点前面的那一个节点叫做前驱节点，为什么要使用这个节点呢，因为使用前驱节点可以保持二叉排序树的性质不变，也就是说代替之后还会是左子树小于根节点，根节点小于右子树。好了前面讲的这些是为了说明为什么需要使用到前驱节点，那么接下来我们来说一下具体的操作细节❣（使用后继节点也可以的）
    • 首先我们需要找到前驱节点，前驱节点就在被删除节点的左子树上，若左子树没有右子树，那么左子树就是前驱节点，将左子树的值给被删除节点，这个时候左子树没用了，变成了要被删除的节点，这个时候就是将左子树的左子树接到被删除节点的左子树上即可。❣橙色代码的操作
    • 如果左子树有右子树，那我们就要找到最右下节点，那个就是前驱节点。
  • 这个时候有两种情况：
    ✔这个节点没有左子树，那么我们直接把它的值给被删除节点，然后把他删了就好了
    ✔这个节点有左子树，那么就要把这个节点的左子树接到他的父节点的右子树上， 也就是❣粉色代码的操作。

💎AVL树（平衡二叉树）
平衡因子:该结点左子树与右子树的高度差

  • 定义：
    • 平衡二叉树左、右子树是平衡二叉树；
    • 所有结点的平衡因子 ≤ 1
  • 数据类型定义
typedef struct node     //记录类型
{
 　KeyType key;    	//关键字项
   int bf;			//增加的平衡因子
   InfoType data;     	//其他数据域
   struct node *lchild,*rchild;//左右孩子指针
} BSTNode;

💟4种调整做法
我们知道，如果要插入一个节点，其插入的节点的平衡因子可能会发生变化，如果>1则需要对他进行平衡调整

  • 有以下四种调整方式，一一展开讲：
    • LL调整
    • LR调整
    • RR调整
    • RL调整
      注意：要调整一定要找到失衡点
      💡LL调整


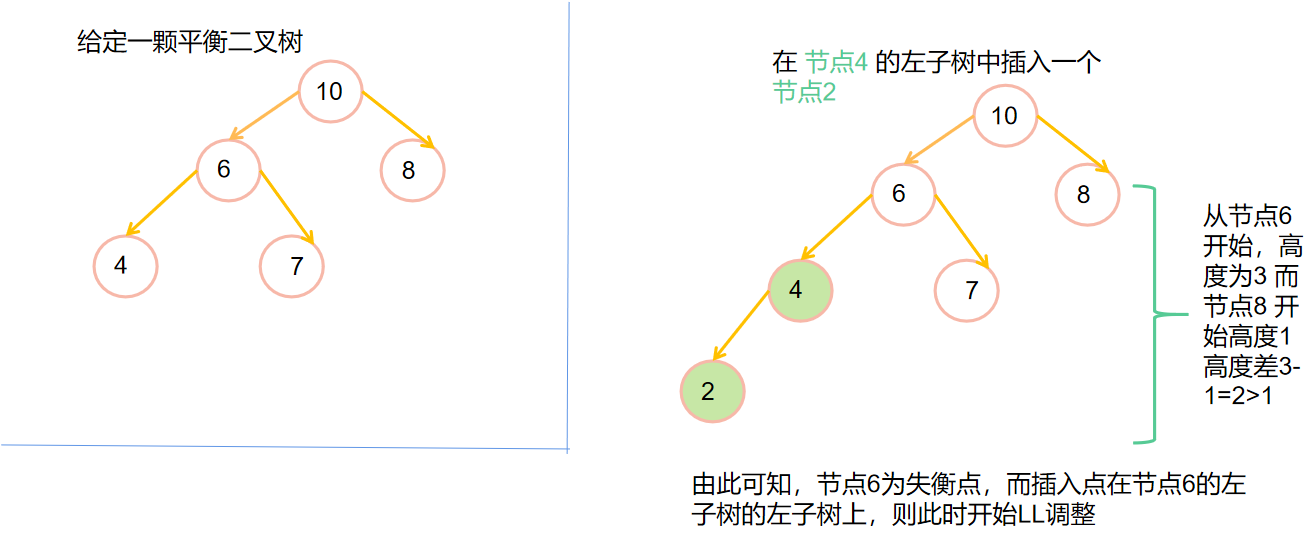
      💡LR调整


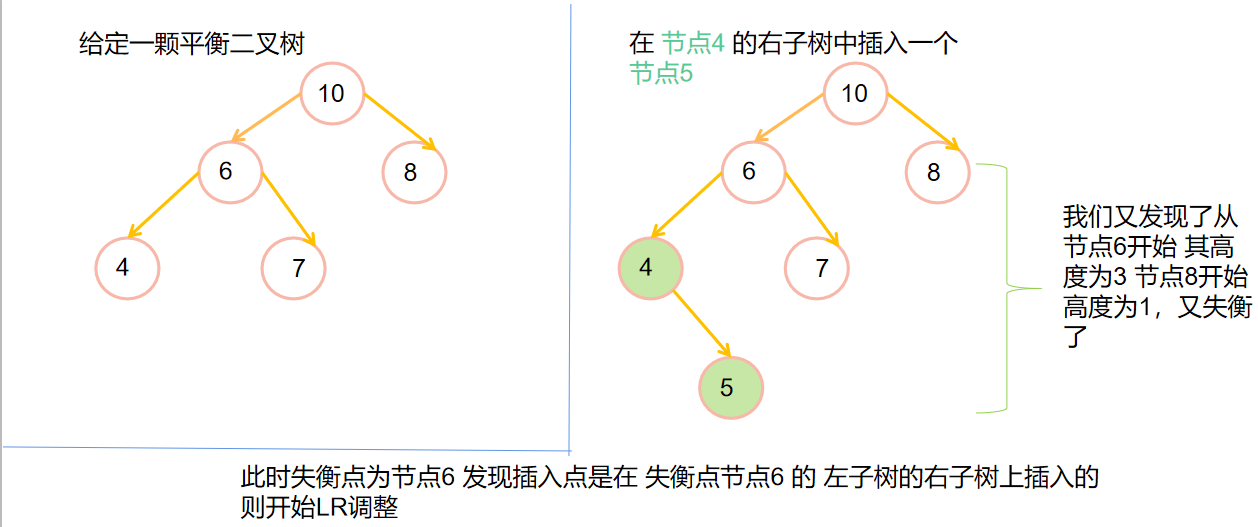
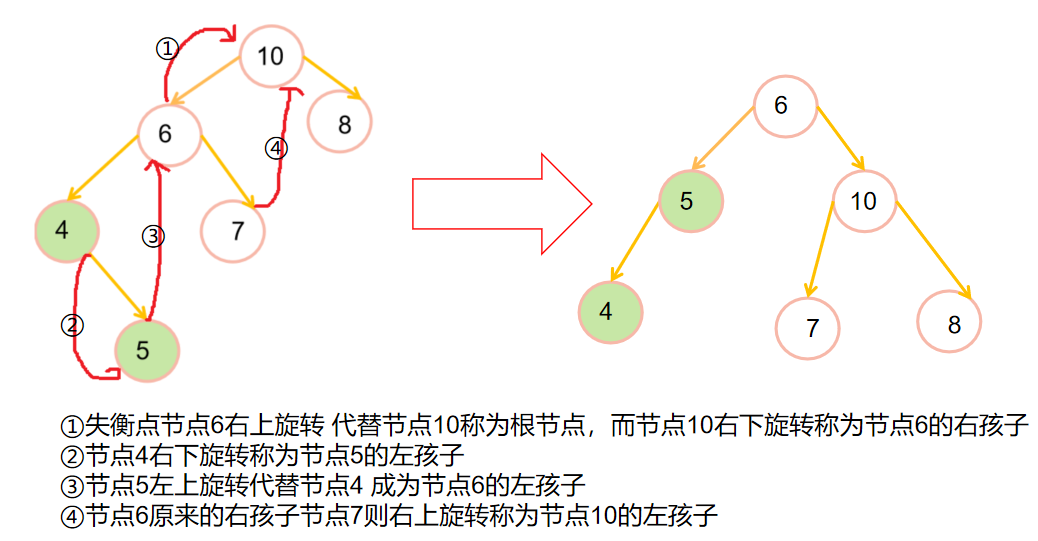
      💡RR调整


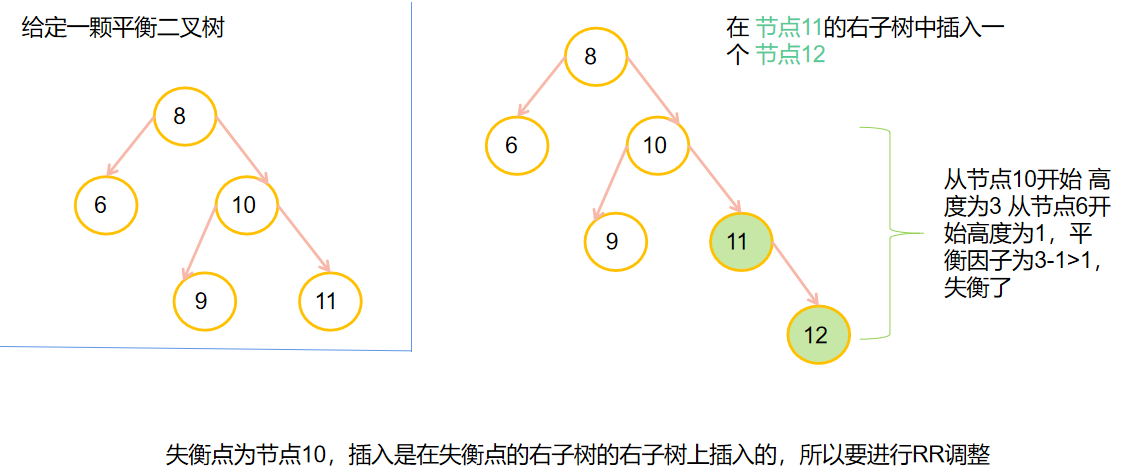
      💡RL调整

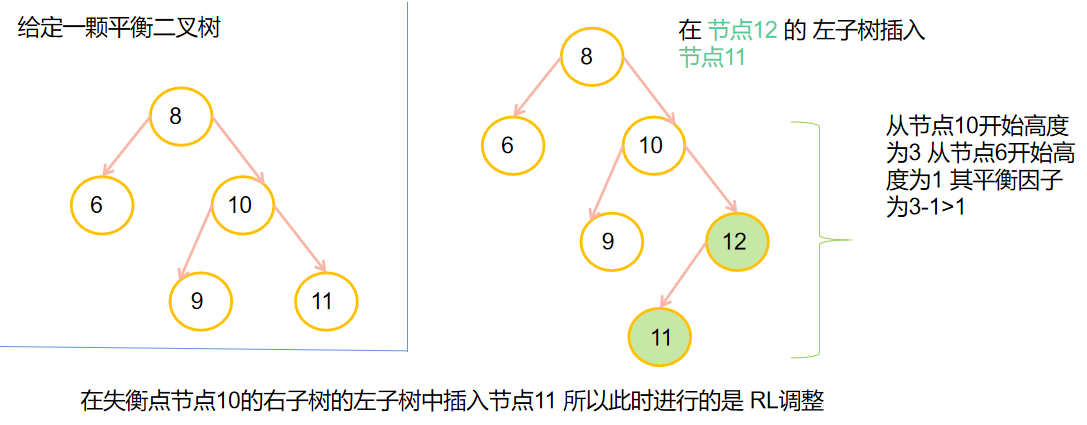
💎B-树和B+树
向上取整：只要有小数，则整数+1
💟B-树

  • 定义：
    • B-树又称作平衡的多路查找树，其所有结点的孩子结点最大值称为B-树的阶，通常用m表示。
    • 一棵m阶B-树或者是一棵空树，或者是满足下列要求的m叉树：
      • 树中的每个结点至多有m颗子树。
      • 若根结点不是叶子结点，则至少有两颗子树。
      • 除根结点外，所有非终端结点至少有m/2（向上取整）颗子树。

非根结点：孩子个数
最小：m/2（向上取整）最大：m
非根结点：关键字个数：
最小：m/2（向上取整） -1 最大：m-1

  • 特点：
    • B-树是所有结点的平衡因子均等于0的多路查找树。所有
      外部结点都在同一层上
    • 在计算B-树的高度时，需要计入最底层的外部结点
    • 外部结点就是失败结点，指向它的指针为空，不含有任何信息，是虚设的。一棵B树中总有n个关键字，则外部结点个数为n+1

🐇B-树的插入
B-树的插入也是建树的过程，或者是查找不成功的时候我们要在指定位置进行插入，插入的位置一定在叶子节点层
我个人认为他采取的也是边查找便插入的过程

  • 需要考虑：
    • 一个结点的关键字个数 n<m-1，不修改指针;（n是关键字个数，m是阶数）
    • 一个结点的关键字个数 n=m-1，则需进行分裂
  • 那么什么是分裂？？
    • 接下来一颗B-树的插入创建过程 注意：每次插入都要从根节点开始比较 比较到叶子节点






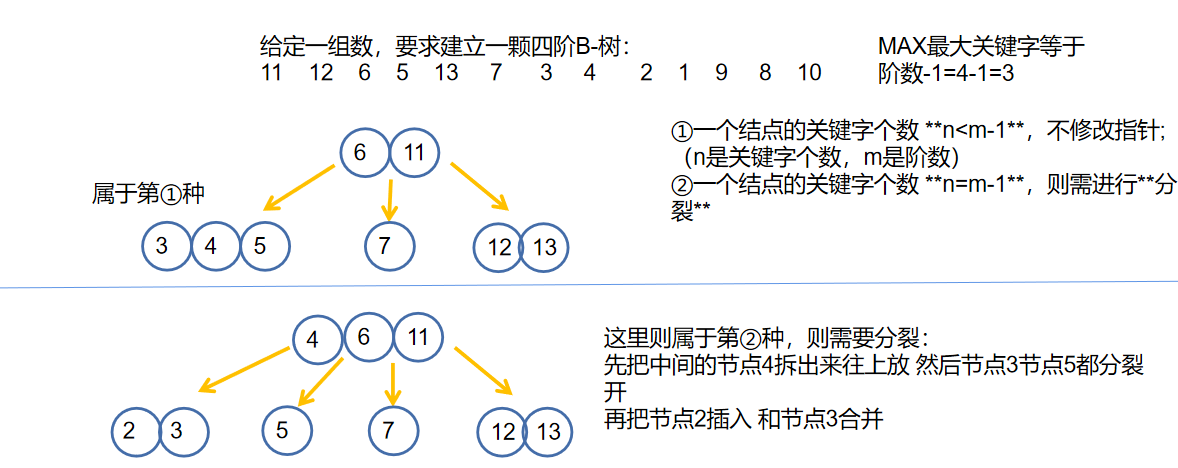
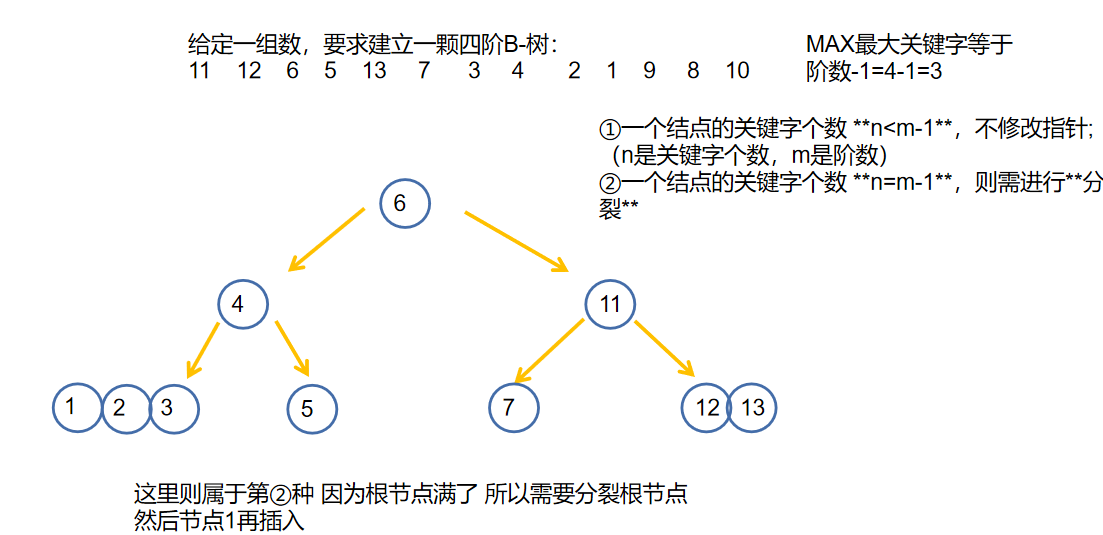
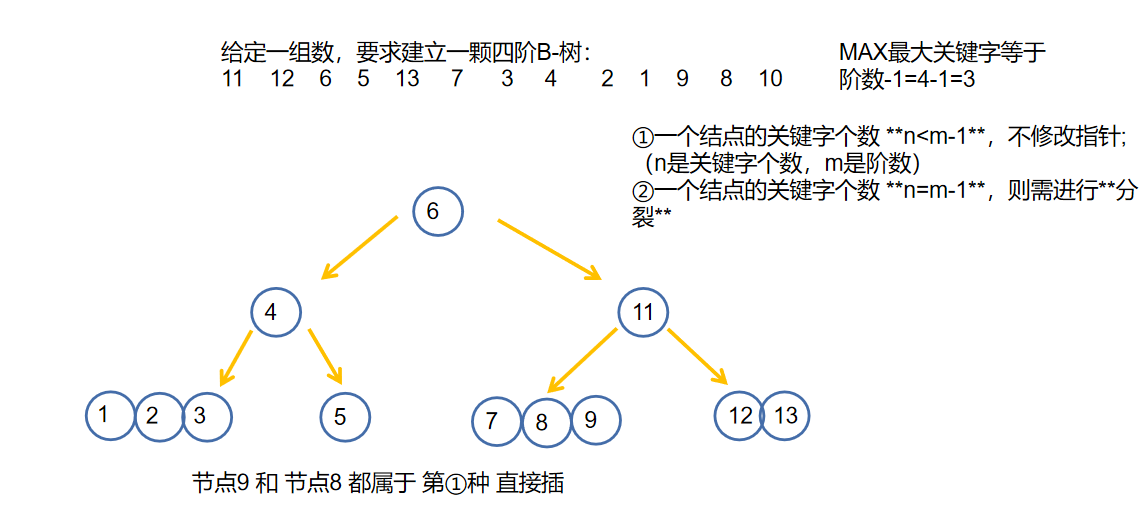
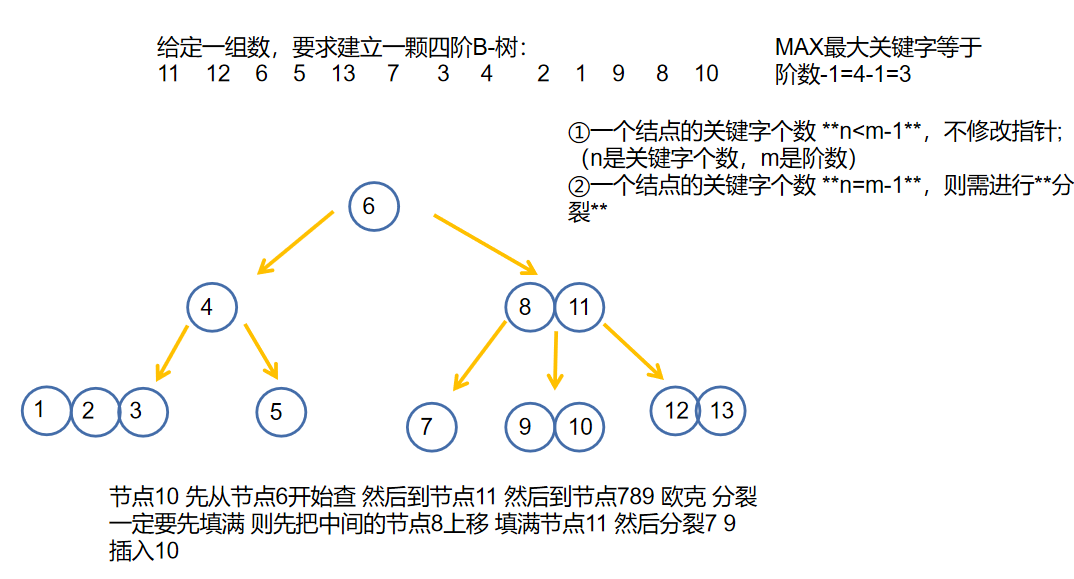
      综上我们可以知道一定要 填满才可分裂！就是一定要上移

🐇B-树的删除

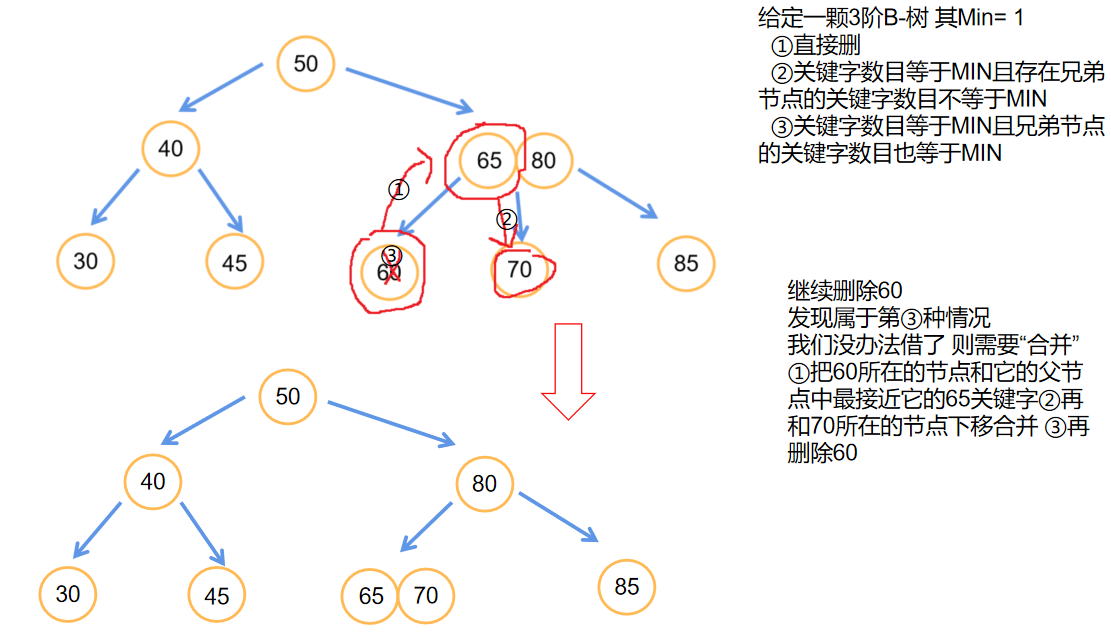
  • B-树的删除则需要看它最少必须有的关键字MIN
  • 分成三种情况
    • 直接删
    • 关键字数目等于MIN且存在兄弟节点的关键字数目不等于MIN
    • 关键字数目等于MIN且兄弟节点的关键字数目也等于MIN
  • 接下来是一颗B-树的删除过程


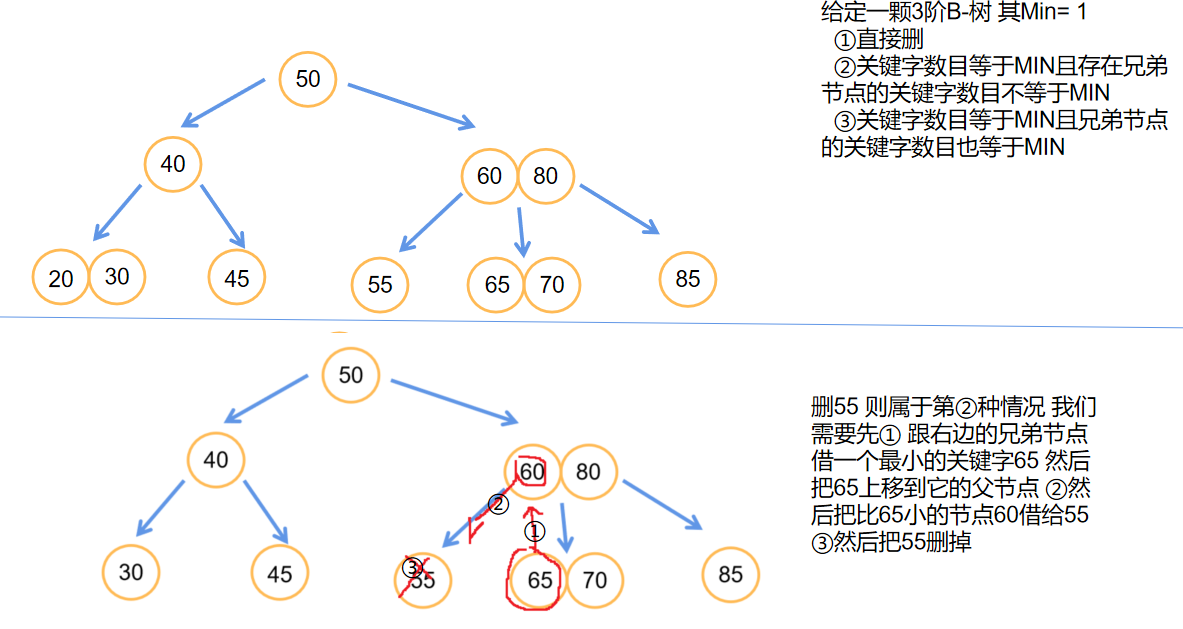
💟B+树（了解即可~）

  • 特征
    • 每个分支节点至多有m棵子树。
    • 根节点或者没有子树，或者至少有两棵子树
    • 除根节点，其他每个分支节点至少有m/2（向上取整）棵子树
    • 有n棵子树的节点有n个关键字。　
    • 所有叶子节点包含全部关键字及指向相应记录的指针
      • 叶子节点按关键字大小顺序链接
      • 叶子节点是直接指向数据文件中的记录。
    • 所有分支节点包含子节点最大关键字及指向子节点的指针。

💎散列查找

说明：
直接算出对象的位置称作散列

  • 散列查找法的两项基本工作：
  • 计算位置：构造散列函数确定关键字存储位置
  • 解决冲突：使用某种策略解决多个关键词位置相同的问题

💕哈希表
哈希表即散列表

  • 如果构造一个散列表？
    • 答案：1.构造散列函数 2.冲突处理

构造散列函数有以下几种做法：
🥞直接定址法

  • 取关键词的某个线性函数值为散列地址
  • 公式：h(key) = a * key + b (a,b为常数，key为关键字）

🥞除留余数法
这个方法算是比较常用的方法，实际上就是把我们的关键词通过求余运算得到散列函数

  • 散列函数：h(key)=key % p
  • p一般为了避免冲突，所以取素数
    • 例如：

🥞数字分析法

  • 分析数字关键字在各位上的变化情况，取比较随机的位置作为散列地址
  • 例如：取11位手机号码key的后四位作为地址：
    • 散列函数为：h(key)=atoi(key+7) char * key

冲突处理有以下几种做法：
🍕开放定址法
若发生了第i次冲突，试探的下一个地址将增加di
di决定了不同的解决冲突方案

  • 线性探测法
  • 平方探测法

🍦线性探测法

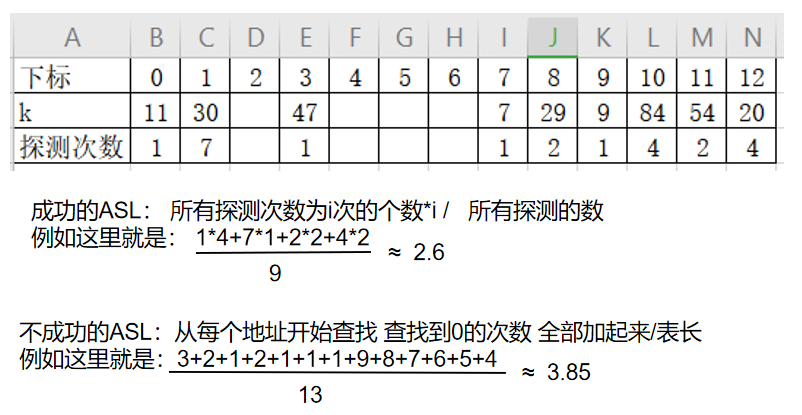
  • 如果发生冲突，则以增量序列 1 2 3 ……循环试探下个储存地址
  • 例如：设关键词序列为
    • 哈希表长=13 装填因子=9/13≈0.69
    • 散列函数：h(key)=key % 11

🍦平方探测法
这里用同一个例子

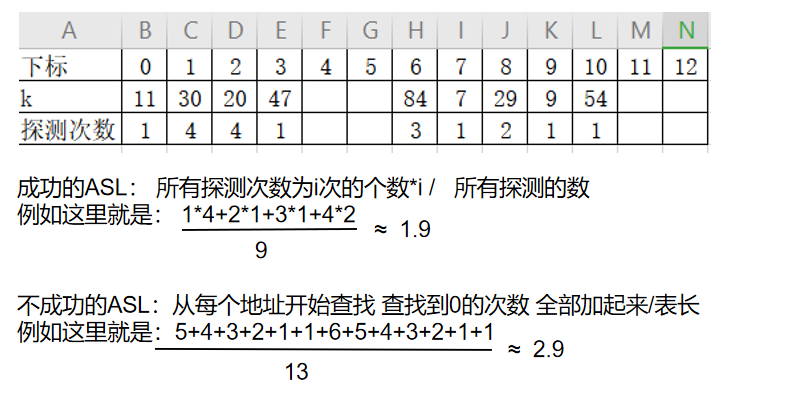
  • 跟线性探测法类似，如果发生冲突，则以增量序列 +1 -1 +2^2 -2^2 ……循环试探下个储存地址
  • 例如：设关键词序列为
    • 哈希表长=13 装填因子=9/13≈0.69
    • 散列函数：h(key)=key % 11

✨哈希表的建立

int InsertHT(HashTable ha,int p,int k,int &n){
    int adr,i;
   adr=k % p;
   if(adr==NULLKEY || adr==DELKEY)    //地址为空，可插入数据
         { ha[adr].key=k;ha[adr].count=1;} 
  else
       { i=1;
        while(ha[adr].key!=NULLKEY && ha[adr].key!=DELKEY)
          {    
             adr=(adr+1) % m; 
              i++;}//查找插入位置
         ha[adr].key=k;ha[adr].count=i;   //找到插入位置 
        }
   n++;
}

💕哈希链

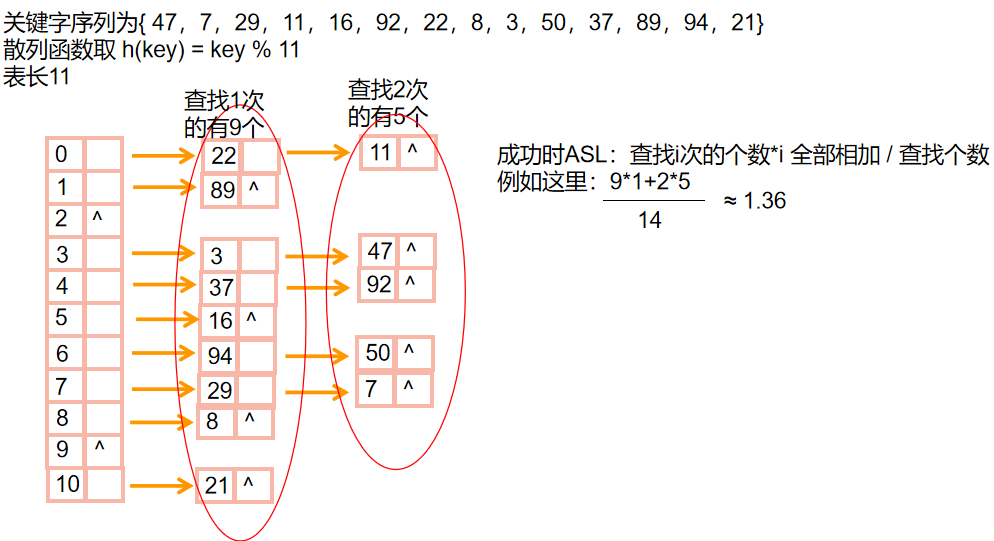
  • 哈希链实际上就是建立建立数组作为下标 然后按照下标分成几条链 把有冲突的关键字指针连成一条链
  • 🎠举个栗子

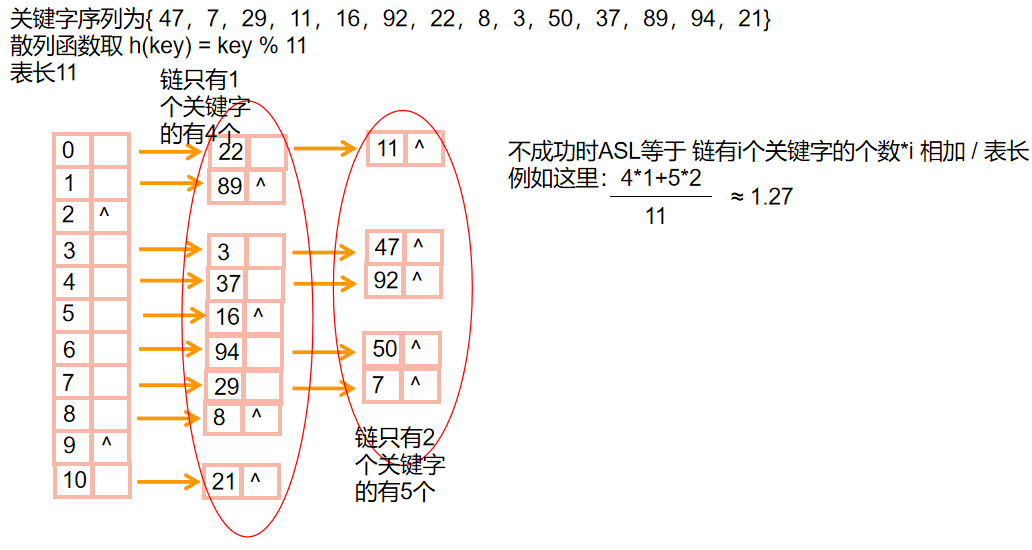
🌺哈希链插入建立

InsertHash(ht,data) 
{
    计算哈希地址adr=data%P；
    查找链ht[adr]，存在不插入。
    不存在：
        data生成数据节点node
        头插法插入链ht[adr]
}
2.哈希链删除数据
InsertHash(ht,data) 
{
    计算哈希地址adr=data%P；
    若链ht[adr]不为空：
          查找链ht[adr]，找到删除
}

1.2.谈谈你对查找的认识及学习体会。

学了顺序查找，二分查找，二叉搜索树，B-，B+树以及哈希，我感觉这些查找方法都是为了提高效率而做的，我们在应用的时候，每种查找都有每种查找的好处，而查找无非离不开增，删。比如我们学二叉搜索树，二叉平衡树的时候，它涉及到的知识点，调整AVL树就是因为增加节点而引起的调整。我觉得其实理解起来说难也不难，就是写代码挺难的吧。这写搜索树都挺像的，都是左边大右边小的所以存在记忆点，我们可以通过一些记忆点然后对知识点进行拓展！

2.PTA题目介绍

2.1 编程题： 二叉搜索树的最近公共祖先🎃

🌺题目

给定一棵二叉搜索树的先序遍历序列，要求你找出任意两结点的最近公共祖先结点（简称 LCA）。

输入格式：

输入的第一行给出两个正整数：待查询的结点对数 M（≤ 1 000）和二叉搜索树中结点个数 N（≤ 10 000）。随后一行给出 N 个不同的整数，为二叉搜索树的先序遍历序列。最后 M 行，每行给出一对整数键值 U 和 V。所有键值都在整型int范围内。

输出格式：

对每一对给定的 U 和 V，如果找到 A 是它们的最近公共祖先结点的键值，则在一行中输出 LCA of U and V is A.。但如果 U 和 V 中的一个结点是另一个结点的祖先，则在一行中输出 X is an ancestor of Y.，其中 X 是那个祖先结点的键值，Y 是另一个键值。如果 二叉搜索树中找不到以 U 或 V 为键值的结点，则输出 ERROR: U is not found. 或者 ERROR: V is not found.，或者 ERROR: U and V are not found.。

输入样例：

6 8
6 3 1 2 5 4 8 7
2 5
8 7
1 9
12 -3
0 8
99 99

输出样例：

LCA of 2 and 5 is 3.
8 is an ancestor of 7.
ERROR: 9 is not found.
ERROR: 12 and -3 are not found.
ERROR: 0 is not found.
ERROR: 99 and 99 are not found.

2.1.1 该题的设计思路💕

  • 建立一个二叉搜索树，u，v为要查询的结点，m,n为查询对数和结点总数，BT是二叉搜索树
  • 这道题我是通过递归和查找来做的，通过三个if查找可以判断u，v是否存在或者不存在，或者一个存在一个不存在
  • 然后使用递归来进行查找祖先，递归这颗树，如果uv都小于BT->data则往左子树走，大于就是右子树，if外面是return，直到递归结束，返回BT->data就是他们的祖先
    • 因为二叉搜索树的特点就是左子树的节点一定都小于根节点，右子树的节点一定都大于根节点，要判断祖先，他们一定都是大于祖先或者小于祖先的
  • 🎀时间复杂度：因为用的是递归查找所以，时间复杂度只跟高度有关
    • O(logN)

2.1.2 该题的伪代码💕

BTree SearchTree(BTree BT, int k);//查找u，v是否存在
BTree IsAncestor(BTree BT, int u, int v);//查找祖先
int main()
{
  int m,n,u,v;
  BTree BT=NULL;
  建树
  for i=0 to m-1//要检查m对 一堆一堆判断
    if(u存在v不存在) 输出
    else if (u不存在v存在) 输出
    else if(u,v都不存在) 输出
    else
    {
      BTree q=BT;
      if(q->data==u) 输出 //u是v的祖先
      else if(q->data==v) 输出//v是u的祖先
      else 都不是 有共同祖先输出  
      end if
    }
 end for
}
BTree IsAncestor(BTree BT, int u, int v)
{
   if(u,v都大于BT->data) 返回BT右子树继续查找uv
   end if
   if(u,v都小于BT->data) 返回BT左子树继续查找uv
   end if
   return BT；
}

2.1.3 PTA提交列表💕

  • ✨Q1:一开始所有答案都是段错误，因为一开始我在创建BT的时候，没有给BT设置为空，导致我在判断祖先的时候树都是空的，树没有成功被建立
  • ✨Q2:第二个问题就是我的格式以及我漏了一种情况，因为一开始我只是考虑了UV可能为互相的祖先，但是漏了UV的祖先也可能是别人，然后就错了，然后就是换行符我给忘记了
  • ✨Q3:第三个问题就是运行超市了，好不容易写出来了结果运行超时，差点以为算法的问题，结果是因为在建树的时候很奇怪

    这样子做是运行超时的

    这样子修改了之后就不超时了。。。。我也不知道为啥

2.1.4 本题设计的知识点💕

  • 二叉搜索树的建树和查找
  • 二叉搜索树的特点

2.2编程题： QQ帐户的申请与登陆🎃

🌺题目

实现QQ新帐户申请和老帐户登陆的简化版功能。最大挑战是：据说现在的QQ号码已经有10位数了。

输入格式:

输入首先给出一个正整数N（≤105），随后给出N行指令。每行指令的格式为：“命令符（空格）QQ号码（空格）密码”。其中命令符为“N”（代表New）时表示要新申请一个QQ号，后面是新帐户的号码和密码；命令符为“L”（代表Login）时表示是老帐户登陆，后面是登陆信息。QQ号码为一个不超过10位、但大于1000（据说QQ老总的号码是1001）的整数。密码为不小于6位、不超过16位、且不包含空格的字符串。

输出格式:

针对每条指令，给出相应的信息：

1）若新申请帐户成功，则输出“New: OK”；
2）若新申请的号码已经存在，则输出“ERROR: Exist”；
3）若老帐户登陆成功，则输出“Login: OK”；
4）若老帐户QQ号码不存在，则输出“ERROR: Not Exist”；
5）若老帐户密码错误，则输出“ERROR: Wrong PW”。

输入样例:

5
L 1234567890 myQQ@qq.com
N 1234567890 myQQ@qq.com
N 1234567890 myQQ@qq.com
L 1234567890 myQQ@qq
L 1234567890 myQQ@qq.com

输出样例:

ERROR: Not Exist
New: OK
ERROR: Exist
ERROR: Wrong PW
Login: OK

2.2.1 该题的设计思路💕

  • 这道题在上个学期写课设的时候也有涉及到登陆注册问题，当时使用的是文件来进行，这个学期学习了map映射之后，可以使用map的函数来进行查找
    • map<类型，类型> 容器名 映射 两个类型变量是一组映射 对应账户密码
    • 容器名.find(类型名) 容器名.end()
      • 用find函数来定位数据出现位置，它返回的一个迭代器，当数据出现时，它返回数据所在位置的迭代器，如果map中没有要查找的数据，它返回的迭代器等于end函数返回的迭代器
  • 综上，我们知道其实这个过程就是map模拟的过程
  • 🎀时间复杂度：O(N)

2.2.2 该题的伪代码💕

int main()
{
   int n;//用户数量
   char command;//命令
   string user，password；//用户名密码
   map<string,string> USER;//映射容器
   输入数量
   while(n--)
      输入命令符和账户密码
      if 命令符是N
         if(账户存在) 不能注册
         else if (账户不存在)
         USER[user]=password;//注册
         输出
      else if(命令符是L)
         if 账户不存在 输出
         else if 账户存在且密码正确 输出
         else 账户存在但密码错误 输出
      end if
}

2.2.3 PTA提交列表💕

  • ✨Q1:在用户登陆的时候，答案错误了，因为在进行判断的时候 我是按照题目的顺序先判断了登陆成功的情况，然后判断用户不存在在判断密码错误的情况，然后发现行不通，就更换了顺序，先判断用户不存在的情况，在判断成功登陆的情况最后判断密码错误的情况。

2.2.4 本题设计的知识点💕

  • map映射的使用

2.3 编程题： 整型关键字的散列映射🎃

🌺题目

给定一系列整型关键字和素数P，用除留余数法定义的散列函数将关键字映射到长度为P的散列表中。用线性探测法解决冲突。

输入格式:

输入第一行首先给出两个正整数N（≤1000）和P（≥N的最小素数），分别为待插入的关键字总数、以及散列表的长度。第二行给出N个整型关键字。数字间以空格分隔。

输出格式:

在一行内输出每个整型关键字在散列表中的位置。数字间以空格分隔，但行末尾不得有多余空格。

输入样例:

4 5
24 15 61 88

输出样例:

4 0 1 3

2.3.1 该题的设计思路💕

  • 使用哈希表来进行线性探测法，使用一个数组S来存放数据和比较得出下标，再把下标赋值给哈希表的数据下标
  • 在处理矛盾的时候和重复数据可以通过一个for循环来break处理
  • 内循环中的j用作线性探测的增量
  • 🎀时间复杂度：O(N^2)

2.3.2 该题的伪代码💕

struct node
{
	int key;	//关键字域
	int Idex;	//下标
}Hash[MAX];		//哈希表类型
int main()
{
   int S[MAX];//存放关键字
   int N,P;//关键字数目和表长
   int i，j,idex；
   for i=0 to N-1 输入哈希数据
   i=0;
   while (N--)
      idex=Hash[i].key%p//算出s数组的下标
      for j=0 to s[(Idex+j)%P]!=0
         if 有重复数据 break
         否则一直j++
      end for
      把哈希表的关键字赋值给s[(idex+j)%P]；
      (idex+j)%P赋值给哈希表的数据域下标
      输出
      i++
   end while
}

2.3.3 PTA提交列表💕

  • ✨Q1:一开始我是在s的下标上出错了我是用的是idex+j 但实际上应该是有(idex+j)%P 要除去表长才能得到最终的下标
  • ✨Q2:如果有重复数据的时候，这里因为我一开始探测增量的时候就只是简单的一个for循环没有任何实质上的东西，而且在判断有无冲突的时候我是用的是if else。就只单纯的让j符合（idex+j）%P的要求，没有考虑到重复数据，后来对这个进行修改，发现if else 很难控制出重复数据，甚至使用了一个if来判断，因为只有一层循环break直接跳出大循环，所以这时候就想到了合并if else 就是直接使用探测增量时候使用的for循环，把处置j=1改为j=0，如果s[(j+idex)%P)不冲突的话 循环也进不去，然后进去循环了之后就可以判断重复数据了，有重复数据就直接跳出就好了
  • ✨Q3:在算法无误的情况下，把赋值搞成了两个等于号，然后怎么样的出的结果都是错的

2.3.4 本题设计的知识点💕

  • 哈希表的构造
  • 线性探测法
posted @ 2020-05-18 09:57  雪梨wink  阅读(364)  评论(0)  编辑  收藏  举报