DS博客作业03--树
0.PTA提交截图

1.本周学习总结
1.1 总结树及串内容
🌈串
- 串即字符串
- 一般记为
str ="a1a2a3...an" - 可以是空串 直接用双引号表示
""中间无空格,空格也是一个字符
- 一般记为
- 子串和主串
- 例如:"BCD"是"ABCD"的子串;主串长度一般大于或等于子串长度;
值得注意的是字符串比较大小的时候 是比较大小即ASCII码的大小而不是比较长短,这样子的比较往往是没有意义的,所以在字符串的应用上,我们更加重视字符串是否相等或者是否匹配
- 例如:"BCD"是"ABCD"的子串;主串长度一般大于或等于子串长度;
🌟BF算法:Brute Force
-
效率低,很朴素
-
其核心思想:查找主串S中字串T的位置 如果S[0]等于T[0]则两两右移 如果S[1]不等于T[1] 那么又开始判断S[1]是否等于T[0] 不等于则S又下移 等于则重复以上步骤 非常的暴力
- 具体如图所示:例如主串是
s="ABCD"字串是t="CD"其查找过程如下
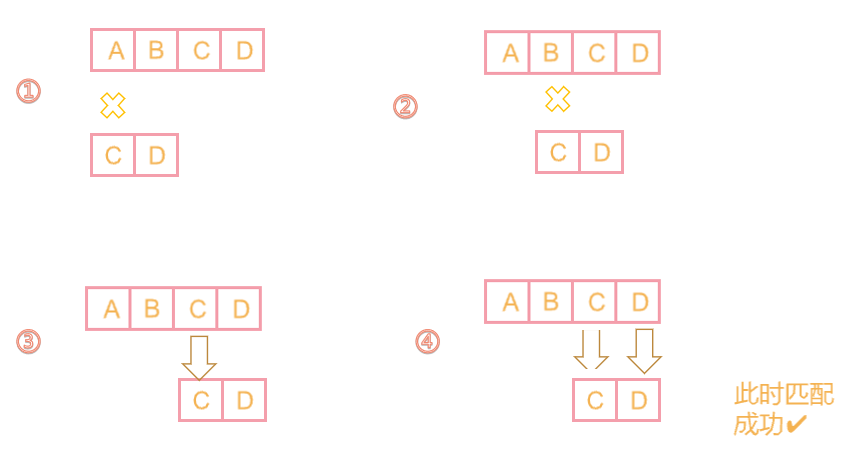
- 具体如图所示:例如主串是
-
具体实现代码
int index(SqString s,SqString t)
{ int i=0, j=0;
while (i<s.length && j<t.length)
{ if (s.data[i]==t.data[j]) //继续匹配下一个字符
{ i++; //主串和子串依次匹配下一个字符
j++;
}
else //主串、子串指针回溯重新开始下一次匹配
{ i=i-j+1; //主串从下一个位置开始匹配
j=0; //子串从头开始匹配
}
}
if (j>=t.length)
return(i-t.length); //返回匹配的第一个字符的下标
else
return(-1); //模式匹配不成功
}
为什么说BF算法的效率低?
- 回溯
- 👼举个栗子: 主串
s="ABCDEFG"子串t="ABCDF"
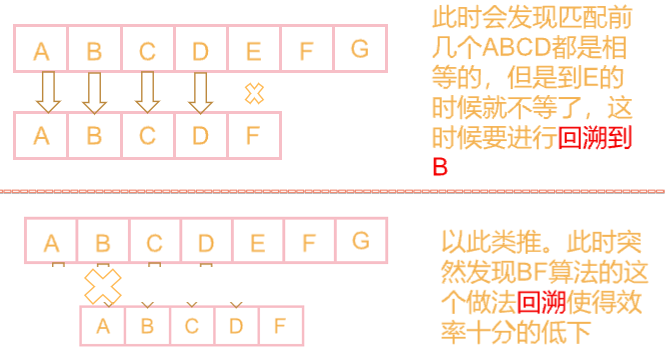
- 👼举个栗子: 主串
🌟KMP算法
由于BF算法效率十分低下 这时候引入了KMP算法 ps:这个算法我也不是很懂,主要是去网上查了一些资料结合老师课件自学的..可能会写错欢迎评论指正
- KMP算法的核心就是避免不必要的回溯,问题由模式串决定,而不由目标串决定
- 重要的是模式串中的前缀和后缀匹配的个数
- 例如:
ssssd假设当匹配到d时发生失配 其前缀和后缀相等的个数就为 (是不是很抽象) 画个图来理解一下

三个相等
- 例如:
- 此时引用k即next数组
- 👼我又来举个栗子啦:

这个匹配过程我就不画了我觉得我描述的挺清楚的哈,电脑画画确实难💡
- 👼我又来举个栗子啦:
- 具体实现代码
int KMPIndex(SqString s,SqString t)
{ int next[MaxSize],i=0,j=0;
GetNext(t,next);
while (i<s.length && j<t.length)
{ if (j==-1 || s.data[i]==t.data[j])
{ i++;
j++; //i,j各增1
}
else j=next[j]; //i不变,j后退
}
if (j>=t.length)
return(i-t.length); //匹配模式串首字符下标
else
return(-1); //返回不匹配标志
}
虽然说KMP算法效率高,但是还是存在缺陷,比如模式串失配位置的元素和前缀元素相等的时候,这时候就出现了nextval数组
🍒next数组改进:nextval数组
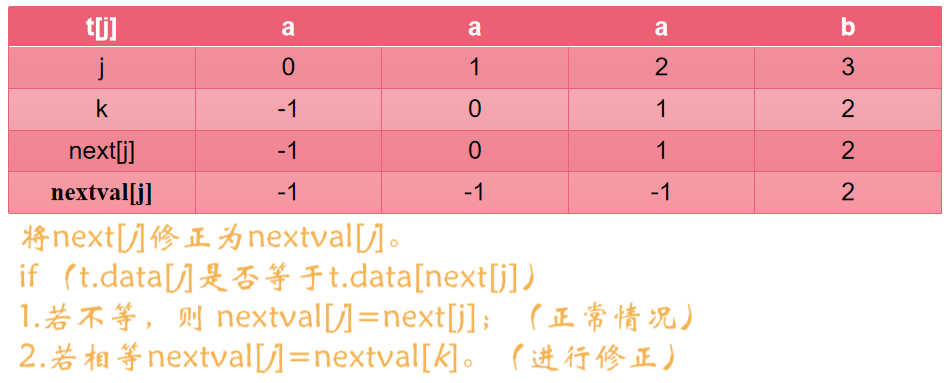
-
匹配时修正j即可
-
获取nextval数组的函数
void GetNextval(SqString t,int nextval[])
{
int j=0,k=-1;
nextval[0]=-1;
while (j<t.length)
{
if (k==-1 || t.data[j]==t.data[k])
{
j++;k++;
if (t.data[j]!=t.data[k]) nextval[j]=k;
else nextval[j]=nextval[k];
}
else
k=nextval[k];
}
}
- 优化后的KMP算法
int KMPIndex1(SqString s,SqString t)
{
int nextval[MaxSize],i=0,j=0;
GetNextval(t,nextval);
while (i<s.length && j<t.length)
{
if (j==-1 || s.data[i]==t.data[j])
{
i++;
j++;
}
else j=nextval[j];
}
if (j>=t.length) return(i-t.length);
else return(-1);
}
🌈树
🍨二叉树
🌳二叉树的定义和性质
- 二叉树的定义:是n(n>=0)个结点的有限集合,它或为空树(n=0),或由一个根结点和两棵称为根的左子树和右子树的,互不相交的二叉树组成。
这定义一看就是递归过程,很晕!注意:二叉树的度一定不超过2,而且具有左右子树之分!!次序不能颠倒,如果只有一颗树一定要区分它是左子树还是右子树哟 - 二叉树的性质:
- 二叉树第i层上的结点数目最多为2i-1(i≥1)。
- 深度为k的二叉树至多有2k-1个结点(k≥1)。
- 在任意一棵二叉树中,若终端结点的个数为n0,度为2的结点数为n2,则n0=n2+1。
🎋满二叉树
- 在一棵二叉树中,如果所有分支节点都存在左子树和右子树,并且所有叶子都在同一层,这样的二叉树称为满二叉树。
- 特点:
- 叶子只能出现在最下一层
- 非叶子结点的度一定是2
- 在同样深度的二叉树中,满二叉树的结点个数一定最多,同时叶子也是最多的
🎋完全二叉树
- 定义:对于一颗具有n个结点的二叉树按层序编号,如果编号为i(1<=i<=n)的结点与同样深度的满二叉树中编号为i的结点位置完全相同,则这棵二叉树称为完全二叉树。
如何理解?:实际上就是满二叉树删除最下面一层右边若干个结点得来的,满二叉树是满的,但是完全二叉树在称为满二叉树之前不会有下一层 - 特点:
- 叶子结点只能出现在最下面两层
- 最下层的叶子结点一定是集中在左部连续位置
- 倒数第二层如果有叶子节点,一定是集中在右部连续位置
- 如果结点的度为1,那么该节点只有左孩子
- 同样节点的二叉树,完全二叉树的深度最小
- 具有n个结点的完全二叉树的深度为log2n+1 log取下限!
- 如果对一颗有n个结点的完全二叉树(其深度为log2n取下限+1)的结点按层序编号,对于任意一节点i(1<=i<=n)有以下性质
①如果i=1,则结点i是二叉树的根,无双亲;如果i>1,则其双亲结点是i/2取整
②如果2i>n,则结点i无左孩子(结点i为叶结点),否则其左孩子是结点2i
③如果2i+1>n,则结点i无右孩子,否则其右孩子结点为2i+1
注意:满二叉树一定是完全二叉树,但是完全二叉树不一定是满二叉树
🎋二叉树排序数
- 一棵空树,或者是具有下列性质的二叉树:
- 若左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 左、右子树也分别为二叉排序树;
- 没有键值相等的结点。
🌳二叉树存储结构、建法、遍历及应用
🎋二叉树的顺序存储结构
- 顺序存储可以用数组来进行存储,只要将二叉树空的部分用空结点或者#补全成一颗完全二叉树即可,数组第一个可以存放#或者-1
- 定义
typedef ElemType BiTree[Max]; - 操作过程如下:

这样的操作极易浪费内存,因为当树结点为空的很多的时候,就会填进去很多个#导致内存浪费,所以这时候引入链式存储结构
- 定义
🎋二叉树的链式存储结构
- 定义:
typedef struct node
{
int data;//数据域
struct node *lchild;//指向左孩子
struct node *rchild;//指向右孩子
}BTree;
- 图示:
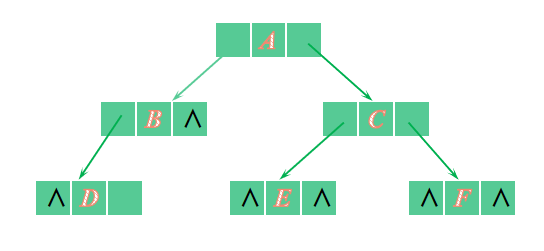
🐾二叉树的创建方法总结
🎋二叉树的顺序存储结构转成二叉链
- 给出一颗二叉树,把它填进数组里然后用#补成满二叉树
- 具体操作如下:
void CreateBTree(BTree &bt,string str, int i)
{
int len;
len = str.size();
bt = new TNode;
if (i > len || i < 1)
{
bt=NULL;return;//停止递归
}
if (str[i] == '#')
{
bt=NULL; return;//填进去
}
bt->data = str[i];//作为新的根节点
CreateBTree(bt->lchild,str, 2 * i);//创建左子树
CreateBTree(bt->rchild,str, 2 * i + 1);//创建右子树
}
- 这种方法比较简单
🎋先序遍历递归建树
- 首先先了解有哪些遍历方式遍历?
💎先序遍历 :一棵树的读入顺序为:根节点->左子树->右子树
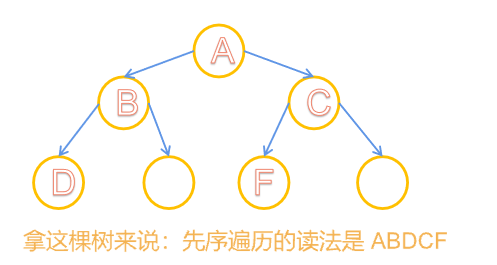
- 先序遍历递归算法
void PreOrder(BTree bt)
{
if (bt!=NULL)
{ printf("%c ",bt->data); //访问根结点
PreOrder(bt->lchild);
PreOrder(bt->rchild);
}
}
💎中序遍历:一棵树的读入顺序为:左子树->根节点->右子树

- 中序遍历递归算法
void InOrder(BTree bt)
{
if (bt!=NULL)
{ InOrder(bt->lchild);
printf("%c ",bt->data); //访问根结点
InOrder(bt->rchild);
}
}
💎后序遍历 :一棵树的读入顺序为:左子树->右子树->根节点
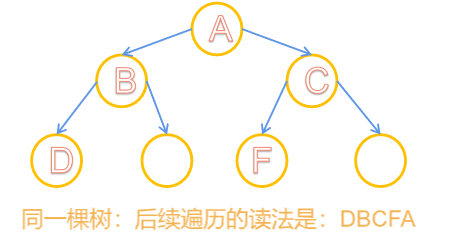
- 后序遍历递归算法
void PostOrder(BTree bt)
{
if (bt!=NULL)
{ PostOrder(bt->lchild);
PostOrder(bt->rchild);
printf("%c ",bt->data); //访问根结点
}
}
💎层序遍历:有点像顺序存储那样子遍历,先依次访问某一层的每个根节点(按顺序),再按照访问顺序分别访问它的左孩子和右孩子
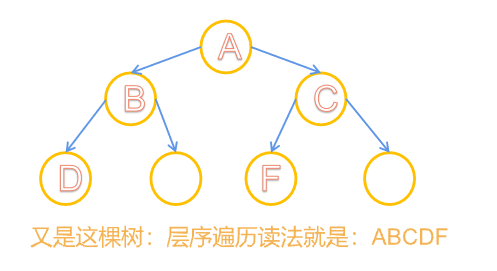
- 此种遍历方式比较,复杂,但是容易读,容易按顺序输出
- 需要引用队列注意:环形队列不可用
- 层序遍历过程:
void LayerOrder(BTreeNode *t)
{
if(t == NULL)return;
queue<BTreeNode*> q;
BTreeNode *temp;
q.push(t);
while(!q.empty())
{
temp = q.front();
q.pop();
cout<<temp->data<<' ';//访问它
if(temp->lchild != NULL)
q.push(temp->lchild);
if(temp->rchild != NULL)
q.push(temp->rchild);
}
}
回到先序遍历建树是不是觉得瞬间眉目舒展
就是那么一回事
BTree CreatTree(string str, int &i)
{
BTree bt;
if (i > len - 1) return NULL;//结束递归
if (str[i] == '#') return NULL;//填空
bt = new BTNode;//申请内存
bt->data = str[i];//访问根节点
bt->lchild = CreatTree(str, ++i);//创建左子树
bt->rchild = CreatTree(str, ++i);//创建右子树
return bt;//递归返回根节点
}
🎋层序遍历建树
- 按层序遍历给定一串树结点例如
A, B, C, D, F, G, I, 0, 0, 0, E, 0, 0, 0 - 空的用来补齐,而且不需要补满,只需要补齐每个结点的左孩子和右孩子即可
- 具体算法
void CreateBTree(BTree &BT,string str)
{
BTree T;int i=0;
queue<BTree> Q;//队列
if( str[0]!='0' ){
BT =new BTNode;
BT->data = str[0];
BT->lchild=BT->rchild=NULL;
Q.push(BT);
}
else BT=NULL; //返回空树
while( !Q.empty())
{
T = Q.front();//从队列中取出一结点
Q.pop();
i++;
if(str[i]=='0' ) T->lchild = NULL;
else //如果有左孩子,则生成新的节点,入队
{
T->lchild = new BTNode;
T->lchild->data = str[i];
T->lchild->lchild=T->lchild->rchild=NULL;
Q.push(T->lchild);
}
i++;
if(str[i]=='0') T->rchild = NULL;
else //如果有右孩子同理
{
T->rchild = new BTNode;;
T->rchild->data = str[i];
T->rchild->lchild=T->rchild->rchild=NULL;
Q.push(T->rchild);
}
}
🎋括号法字符串构造二叉树
- 碰到左括号表示左孩子,逗号表示右孩子,右括号则出栈
- 具体算法
void CreateBTNode(BTNode * &b,char *str)
{ //由str 二叉链b
BTNode *St[MaxSize], *p;
int top=-1, k , j=0;
char ch;
b=NULL; //建立的二叉链初始时为空
ch=str[j];
while (ch!='\0') //str未扫描完时循环
{ switch(ch)
{
case '(': top++; St[top]=p; k=1; break; //可能有左孩子结点,进栈
case ')': top--; break;
case ',': k=2; break; //后面为右孩子结点
default: //遇到结点值
p=(BTNode *)malloc(sizeof(BTNode));
p->data=ch; p->lchild=p->rchild=NULL;
if (b==NULL) //p为二叉树的根结点
b=p;
else //已建立二叉树根结点
{ switch(k)
{
case 1: St[top]->lchild=p; break;
case 2: St[top]->rchild=p; break;
}
}
}
j++; ch=str[j]; //继续扫描str
}
}
🐾二叉树的应用
表达式树
- 具体思路是:
void InitExpTree(BTree &T, string str)
建立两个栈,一个运算符栈一个树根栈
stack<BTree> num;stack<char> op;
然后在运算符栈里存入一个‘#’ 作用是为了控制第一个运算符直接存入以及表达式结束后 建树的操作控制循环条件
while(str[i])
if 是操作数 就直接创建一个树节点 令T->data=操作数 左右子树置空
i++;
else 是运算符
if str[i]的优先级<栈顶运算符
直接让运算符入栈 i++;
else if str[i]的优先级>栈顶运算符
开始建树节点 让运算符栈顶=T->data;
左右子树分别等于从数根栈中弹出的两个树节点
i++;
else if 两个符号优先级相等
运算符栈出栈;i++;
end if
end if
end while //表达式遍历完后
//开始利用两个栈进行建树操作
while(op.top()!=’#’)//‘#’为建树结束标志
建树操作跟str[i]的优先级>栈顶运算符的操作一样
end while
double EvaluateExTree(BTree T)//计算
后序遍历这棵树的左右节点用左右节点进行+-*/
注意除法的时候要注意除数为0的情况
还有判断数是否是空树以及字符数转化数字的操作
注意:控制第一个字符以及下面表达式二叉树的建立我用的是 判断运算符栈是否为空和两个栈是否为空,但是怎么都不行,跟同学讨论了一下知道了使用‘#’来控制的办法,把这个万恶的错误给改了
🍨普通树
🎋树结构
- 双亲存储结构
- 根据双亲表示法节点结构定义
typedef struct BTNode
{
ElemType data; //存放树中结点的数据
int parent; //存放双亲下标
}BTNode;
typedef struct
{
CTBox nodes[MAX_TREE_SIZE];
int r; //根的位置
int n; //结点的总数
}BTree;
- 其存放
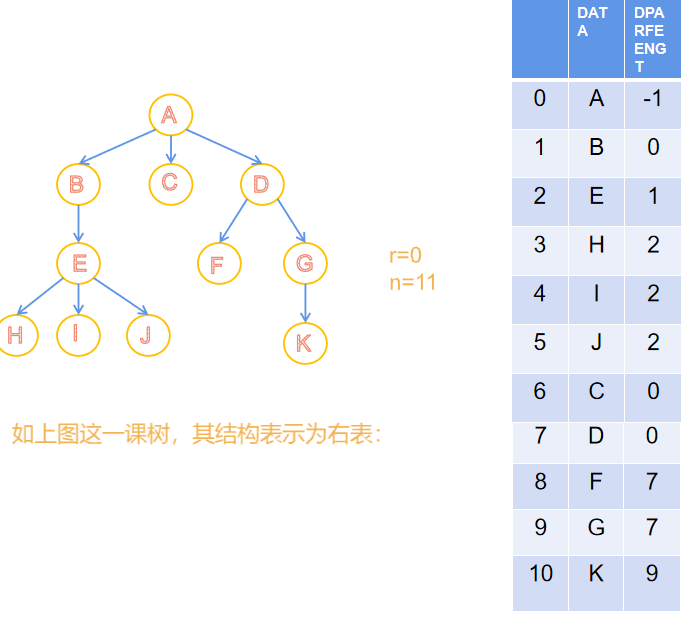
存放顺序为先序遍历。 - 这样的存储结构,我们可以通过结点的parent指针找到他的双亲结构,时间复杂度为O(1),当parent=-1时就是树结点的根
- 我们可以通过改变BTNode的结构,增加,然后可以增加孩子1或者孩子2;可以关注到它的孩子。
- 也可以给它的结构,给结构加个部分就是兄弟啥的,就可以指向兄弟
个人觉得很灵活
则引入孩子兄弟表示法
🎋孩子兄弟表示
typedef struct tnode
{
ElemType data;//结点的值
struct tnode *son;
struct tnode *brother;
}TSBNode;
- 二叉树是指向左子树右子树,而这里的两个结点一个指向兄弟一个指向孩子
🐾树的创建
🎋双亲表示法的创建
PTree InitPNode(PTree tree)
{
int i,j;
char ch;
//printf("请输出节点个数:\n");
scanf("%d",&(tree.n));
//printf("请输入结点的值其双亲位于数组中的位置下标:\n");
for(i=0; i<tree.n; i++)
{
fflush(stdin);
scanf("%c %d",&ch,&j);
tree.tnode[i].data = ch;
tree.tnode[i].parent = j;
}
return tree;
}
🎋孩子表示法的创建
CTree initTree(CTree tree)
{
printf("输入节点数量:\n");
scanf("%d",&(tree.n));
for(int i=0;i<tree.n;i++)
{
printf("输入第 %d 个节点的值:\n",i+1);
fflush(stdin);
scanf("%c",&(tree.nodes[i].data));
tree.nodes[i].firstchild=(ChildPtr*)malloc(sizeof(ChildPtr));
tree.nodes[i].firstchild->next=NULL;
printf("输入节点 %c 的孩子节点数量:\n",tree.nodes[i].data);
int Num;
scanf("%d",&Num);
if(Num!=0)
{
ChildPtr * p = tree.nodes[i].firstchild;
for(int j = 0 ;j<Num;j++)
{
ChildPtr * newEle=(ChildPtr*)malloc(sizeof(ChildPtr));
newEle->next=NULL;
printf("输入第 %d 个孩子节点在顺序表中的位置",j+1);
scanf("%d",&(newEle->child));
p->next= newEle;
p=p->next;
}
}
}
return tree;
}
🎋双亲孩子表示法的创建
void InitCtree(CTree &t) //初始化树
{
int i;
printf("请输入树的结点个数:\n");
scanf("\n%d",&t.n);
printf("依次输入各个结点:\n");
for(i=0; i<t.n; i++)
{
fflush(stdin);
t.tree[i].data = getchar();
t.tree[i].r = 0;
t.tree[i].firstchid = NULL;
}
}
void AddChild(CTree &t) //添加孩子
{
int i,j,k;
printf("添加孩子\n");
for(k=0; k<t.n-1; k++)
{
fflush(stdin);
printf("请输入孩子结点及其双亲结点的序号:\n");
scanf("%d,%d",&i,&j);
fflush(stdin);
CNode *p = (CNode *)malloc(sizeof(CNode));
p->childnode = i;
p->nextchild = NULL;
t.tree[i].r = j; //找到双亲
if(!t.tree[j].firstchid)
t.tree[j].firstchid = p;
else
{
CNode *temp = t.tree[j].firstchid;
while(temp->nextchild)
temp = temp->nextchild;
temp->nextchild = p;
}
}
}
🎋孩子兄弟表示法的创建
void creat_cstree(CSTree &T)
{
FILE *fin=fopen("树的孩子兄弟表示法.txt","r");
char fa=' ',ch=' ';
for( fscanf(fin,"%c%c",&fa,&ch); ch!='#'; fscanf(fin,"%c%c",&fa,&ch) )
{
CSTree p=(CSTree)malloc(sizeof(CSTree));
init_cstree(p);
p->data=ch;
q[++count]=p;
if('#' == fa)
T=p;
else
{
CSTree s = (CSTree)malloc(sizeof(CSTree));
int i;
for(i=1;i<=MAXSIZE;i++)
{
if(q[i]->data == fa)
{
s=q[i];
break;
}
}
if(! (s->firstchild) ) //如果该双亲结点还没有接孩子节点
s->firstchild=p;
else //如果该双亲结点已经接了孩子节点
{
CSTree temp=s->firstchild;
while(NULL != temp->nextsibling)
{
temp=temp->nextsibling;
}
temp->nextsibling=p;
}
}
}
fclose(fin);
}
🐾树的遍历
- 先根遍历:类似先序遍历,都是先访问根节点,然后按照次序一步一步往右移动,会先序遍历的人应该很容易理解先根遍历,这里就不绘图啦
- 后根遍历:类似后序遍历,按照顺序树的下面开始遍历 根都是最后访问的,总根在最后一个,注意一定是树不空的时候
- 层次遍历:哈哈这个是最有次序的与二叉树的层次遍历同理从上到下,然后从左到右
🍨线索二叉树和双向线索二叉树
🐾线索二叉树
- 我们的二叉树链不是每个结点都会用到,有的结点会造成浪费,而且由于二叉树条条路都走到黑,导致没有我们不知道它前驱后继,我们可以引入利用这个空的结点来记录前驱和后继
这时候就出现了线索二叉树- 这时候我们要考虑一下线索二叉树用什么遍历方式最好呢?只是说中序遍历线索二叉树更好,但是先序后序遍历也是欧克的啦。
答案:中序遍历 理由如下
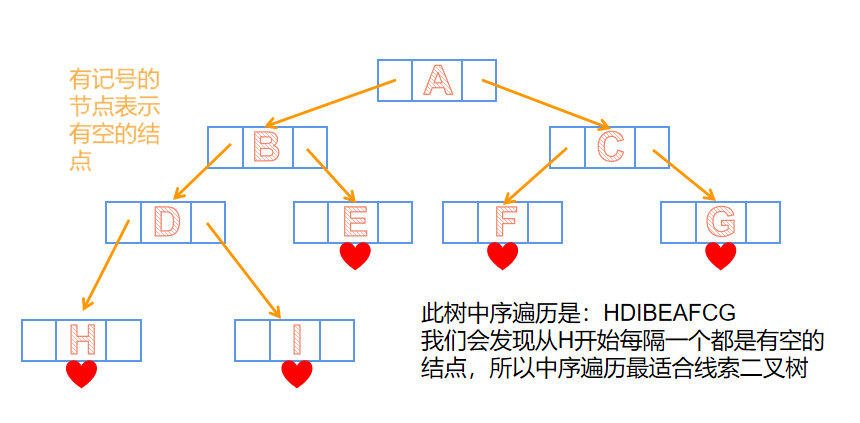
思路很简单:
- 这时候我们要考虑一下线索二叉树用什么遍历方式最好呢?只是说中序遍历线索二叉树更好,但是先序后序遍历也是欧克的啦。
- 如果左子树为空,则存放指向中序遍历序列中该结点的前驱结点。这个结点称为该结点的中序前驱;
- 如果右子树为空,则存放指向中序遍历序列中该结点的后继结点。这个结点称为该结点的中序后继;
🐾双向线索二叉树
- 这些空结点可以指向它的前驱和后继,当然也不是所有遇到的中序遍历每隔一个都有两个空的结点啦。
- 于是就有了双向线索二叉树,我们只需要对这个定义进行扩容,加上ltag和rtag即可
- 定义:
typedef struct node
{
ElemType data; //结点数据域
int ltag,rtag; //增加的线索标记
struct node *lchild; //左孩子或线索指针
struct node *rchild; //右孩子或线索指针
}TBTNode;
ltag,rtag的作用,当它们为0的时候分别指向左孩子和右孩子,当ltag为1时指向前驱,rtag为1的时候指向其后继
- 我这里拿中序遍历做个示范,其它同理,线索用虚线表示。
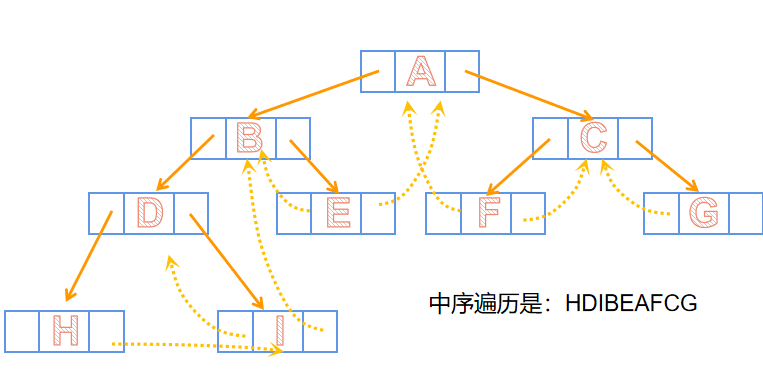
- 中序线索二叉树创建
TBTNode *pre; //全局变量
TBTNode *CreatThread(TBTNode *b) //中序线索化二叉树
{ TBTNode *root;
root=(TBTNode *)malloc(sizeof(TBTNode)); //创建头结点
root->ltag=0; root->rtag=1; root->rchild=b;
if (b==NULL) root->lchild=root; //空二叉树
else
{ root->lchild=b;
pre=root; //pre是*p的前驱结点,供加线索用
Thread(b); //中序遍历线索化二叉树
pre->rchild=root; //最后处理,加入指向头结点的线索
pre->rtag=1;
root->rchild=pre; //头结点右线索化
}
return root;
}
void Thread(TBTNode *&p) //对二叉树b进行中序线索化
{ if (p!=NULL)
{
Thread(p->lchild); //左子树线索化
if (p->lchild==NULL) //前驱线索化
{ p->lchild=pre; p->ltag=1; } //建立当前结点的前驱线索
else p->ltag=0;
if (pre->rchild==NULL) //后继线索化
{ pre->rchild=p;pre->rtag=1;} //建立前驱结点的后继线索
else pre->rtag=0;
pre=p;
Thread(p->rchild); //递归调用右子树线索化
}
}
🍨哈夫曼树和哈夫曼编码
🐾哈夫曼树
- 二叉树的带权路径长度
- 就是每个结点的值(即权值)和根结点到它的路径(这个路径就是层数-1)相乘的和
- wpl=wili求和(i>=1)
- 哈夫曼树就是最优解,即带权路径长度最短的树
🐾哈夫曼树的构建 - 原则:
- 权值越大的叶结点越靠近根结点。
- 权值越小的叶结点越远离根结点。
-方法: - 把需要建的东西都放到一个集合里,每次都取最小的两个权值建成一棵树,这棵树的根节点的权值是这两个最小的权值相加得到的,然后把这两个最小的值在原来的集合里删去,再把根节点的这个权值放进集合里,再重新找两个最小的来建树,到最后集合里只剩下一棵树,这棵树即是哈夫曼树啦
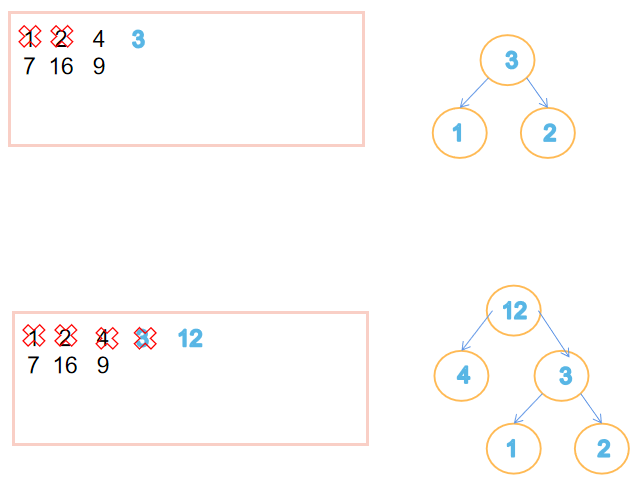
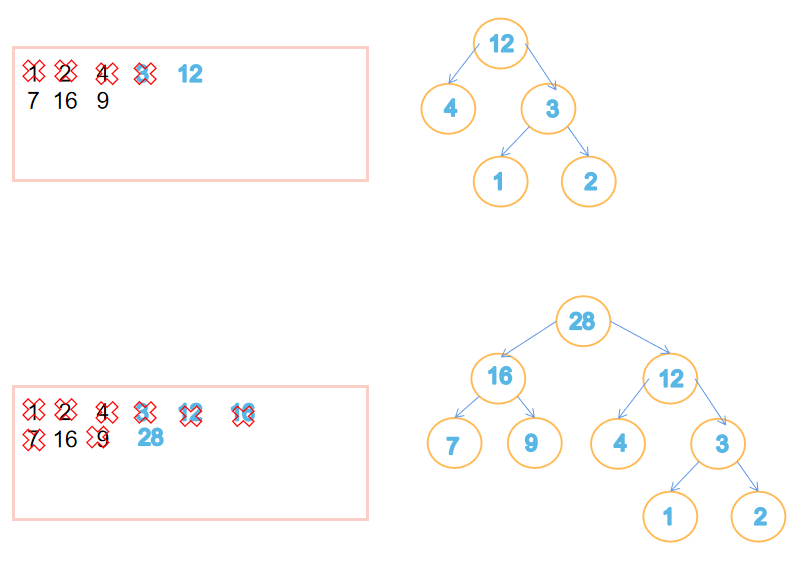
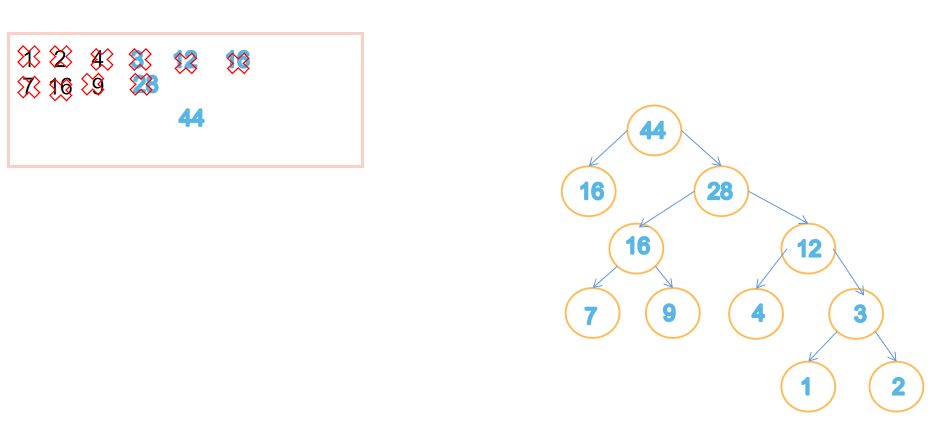
🐾哈夫曼编码
- 哈夫曼编码就是为了使得编码长度最短而出现的
- 哈夫曼编码有个性质就是一个编码不可能等于另一个编码的前缀。
- 哈夫曼编码依靠给出的字母出现的的频率,利用这个频率来进行建哈夫曼树的。
- 然后根据往左走和往右走可以分别在路径上写上0和1 得出来的就是哈夫曼编码
- 平均码长等于其wpl/出现总次数
- 哈夫曼编码求法
void CreateHCode(HTNode ht[],HCode hcd[],int n)
{ int i,f,c; HCode hc;
for (i=0;i<n;i++) //根据哈夫曼树求哈夫曼编码
{ hc.start=n;c=i; f=ht[i].parent;
while (f!=-1) //循环直到无双亲节点即到达树根节点
{ if (ht[f].lchild==c) //当前节点是左孩子节点
hc.cd[hc.start--]='0';
else //当前节点是双亲节点的右孩子节点
hc.cd[hc.start--]='1';
c=f;f=ht[f].parent; //再对双亲节点进行同样的操作
}
hc.start++; //start指向哈夫曼编码最开始字符
hcd[i]=hc;
}
🍨并查集
- 并查集特别适合找关系,等于就是把一堆人或者一堆东西,分成一个个集合,每一个集合代表一棵树
- 要判断某个人和某个人或者某个东西和某个东西是否有关系,那就层层递归,分别找他们的根节点,如果根节点一样,这两个东西或者两个人就有关系
- 根节点就意味着是老大
- 并查集从另一个意义上来讲就是一个集合森林
- 存储结构:
typedef struct node
{
int data; //结点对应人的编号
int rank; //结点秩:子树的高度,合并用
int parent; //结点对应双亲下标
} UFSTree; //并查集树的结点类型
- 说明:
- 一开始的双亲都指向自己,秩都初始化为0
🤞要形成一个集合,肯定是要先合并,形成一个关系网才能进行查找根,判断关系~
那么合并操作怎么做呢!
🍨两个元素各自所属的集合的合并
- 基本思路在于,谁的轶比较大谁就当另一个的老大,啊呸是双亲
void UNION(UFSTree t[],int x,int y) //将x和y所在的子树合并
{
x=FIND_SET(t,x); //查找x所在分离集合树的编号
y=FIND_SET(t,y); //查找y所在分离集合树的编号
if (t[x].rank>t[y].rank) //y结点的秩小于x结点的秩
t[y].parent=x; //将y连到x结点上,x作为y的双亲结点
else //y结点的秩大于等于x结点的秩
{ t[x].parent=y; //将x连到y结点上,y作为x的双亲结点
if (t[x].rank==t[y].rank) //x和y结点的秩相同
t[y].rank++; //y结点的秩增1
}
}
🍨查找一个元素所属的集合
- 基本思路:这一个找老大的过程,找到最上一层的那一个根结点,返回它~
int FIND_SET(UFSTree t[],int x) //在x所在子树中查找集合编号
{
if (x!=t[x].parent) //双亲不是自已
return(FIND_SET(t,t[x].parent)); //递归在双亲中找x
else
return(x); //双亲是自已,返回x
}
1.2.谈谈你对树的认识及学习体会。
难啊,递归搞不懂啊,而且概念说不上复杂就是很多,容易搞混,比如什么线索二叉树双向线索二叉树,晕乎乎的,刷题刷了也不一定会写呀,我翻阅了比较多的资料,就感觉自己的知识比较浅薄,而且我觉得这个对于数学思维要求还是挺高的,就是数学学得好,理解起来会更简单,但是我是属于,图会画,大致上也知道是个什么东西,可是敲代码来我就是个废物。唉,还是要多练把,可以在力扣上找一些简单题写写看,或者看看别人的代码是怎么写的。每次看到别人写递归我觉得我是个弟弟。
2.阅读代码
2.1 树的子结构
🍓题目
输入两棵二叉树A和B,判断B是不是A的子结构。(约定空树不是任意一个树的子结构)
B是A的子结构, 即 A中有出现和B相同的结构和节点值。
例如:
给定的树 A:3 / \4 5
/
1 2
给定的树 B:4
/
1
返回 true,因为 B 与 A 的一个子树拥有相同的结构和节点值。示例 1:
输入:A = [1,2,3], B = [3,1]
输出:false
示例 2:输入:A = [3,4,5,1,2], B = [4,1]
输出:true
🍓解题代码
class Solution {
public:
bool helper(TreeNode* A, TreeNode* B) {
if (A == NULL || B == NULL) {
return B == NULL ? true : false;
}
if (A->val != B->val) {
return false;
}
return helper(A->left, B->left) && helper(A->right, B->right);
}
bool isSubStructure(TreeNode* A, TreeNode* B) {
if (A == NULL || B == NULL) {
return false;
}
return helper(A, B) || isSubStructure(A->left, B) || isSubStructure(A->right, B);
}
};
2.1.1 该题的设计思路
使用了递归的方法在A中寻找和B根节点数据域相同的节点,当A和B都为空的时候返回false,因为题目约定空树不是任意一个树的子结构。当A,B都不为空的时候,一边进行A左右孩子的遍历,一边比较A与B的数据域。在比较数据域时,若两者指针都为空则代表两者在此处都没有数据存放,返回true,当数据域不相等时,则不符合题意,返回false,当相等时则使用递归继续比较各自左右孩子的数据域。将A与B比较的结果返回到isSubStructure函数中,若有一处返回true则证明B是A的子结构
- 时间复杂度:O(n^2);n为A的节点数
- 空间复杂度:O(h^2);h为A树的高度
2.1.2 该题的伪代码
bool isSubStructure(TreeNode* A, TreeNode* B){
if(A为空或者B为空)返回false;
返回helper(A,B)或isSubStructure( A->left,B)或isSubStructure( A->right,B);
}
bool helper(TreeNode* A,TreeNode* B){
if(A为空且B也为空)返回true;
if(A不为空或者B不为空)返回false;
返回(A->val==B->val)&&(isSameTree(A->left,B->left)&&isSameTree(A->right,B->right));
}
2.1.3 运行结果
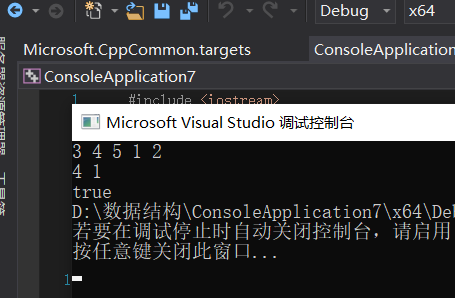
2.1.4分析该题目解题优势及难点。
- 该题目的解题使用了递归,缩短了代码长度,每一步的目的都很清晰,能让阅读者对代码易懂。
- 但是也在郧西过程当中会有许多多余的步骤。
- 题目难点在于需要先在A中找到与B根节点相同的节点,然后两者再进行结构数值上的比较,对于递归要求比较灵活的运用,并且需要对树空的情况加以区分。
2.2 验证二叉搜索树
🍓题目
给定一个二叉树,判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征:
节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。示例 1:
输入:
2
/
1 3
输出: true示例 2:
输入:
5
/
1 4
/
3 6
输出: false
解释: 输入为: [5,1,4,null,null,3,6]。
根节点的值为 5 ,但是其右子节点值为 4 。
🍓解题代码
bool fun(struct TreeNode* root, long low, long high) {
if (root == NULL) return true;
long num = root->val;
if (num <= low || num >= high) return false;
return fun(root->left, low, num) && fun(root->right, num, high);
}
bool isValidBST(struct TreeNode* root){
return fun(root, LONG_MIN, LONG_MAX);
}
2.2.1 该题的设计思路
- 对于每个节点值val,设其最低和最高的边界为low , high,用 long 长整型来防止INT_MAX溢出
- 判断根结点时,条件是val必须大于low,而且小于high ,否则返回 false
- 判断左右孩子的时候
- 左孩子的话是low要变化,因为左孩子只能比根节点要小,都比每次的根节点要小,新的low为high与val更小的那个数。但是因为是二叉搜索树所以val必小于high,所以新的low=val
- 右孩子的话是high要变化,因为右孩子只能比根节点大,比每次的根节点也都要大,新的high为low与val更大的那个数,但是同理,val肯定大于low,所以新的high=val
- 时间复杂度:O(n)
- 空间复杂度:O(n)
2.2.2 该题的伪代码
bool fun(struct TreeNode* root, long low, long high)
{
if 根节点是空 return 真
end if
if 根的值小于low或者根的值大于high return 假
end if
然后递归
return fun(左子树作为新的根传进去,又开始比较)&&(比较左子树又比较右子树)
}
2.2.3 运行结果
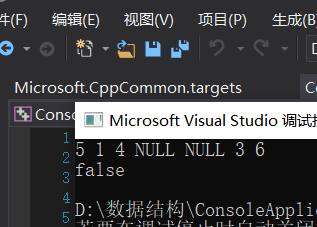
2.2.4分析该题目解题优势及难点。
- 这个代码是我对比其他的代码更加的简洁易懂,就觉得挺强的,思路也很简洁,因为二叉搜索树肯定是越往下根节点要么越大要么越小,不然就直接返回false,这个递归就可以做到这点,low和high运用十分巧妙,代码量也少
- 此题目的难点就在于,因为每次low和high都是要进行变化的,可是怎么变化,一定要有一个新的思路,不然就无法进行递归,这里传参直接传进num即结点val的值,就是已经在思路理由了,根据二叉搜索树的性质来进行判断新的low和high,我觉得一般人难有这种做法,所以写这个代码的人不是一般人。
2.3 重建二叉树
🍓题目
输入某二叉树的前序遍历和中序遍历的结果,请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
例如,给出
前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]返回如下的二叉树:
3/
9 20
/
15 7
🍓解题代码
TreeNode* reConstructBinaryTree(vector<int> pre,vector<int> vin)
{
if(pre.empty())return nullptr;
if(vin.empty())return nullptr;
int idx=0;
vector<int>vin_left;
vector<int>vin_right;
vector<int>pre_left;
vector<int>pre_right;
for(int i=0;i<vin.size();i++)
{
if(idx)
{
vin_right.push_back(vin[i]);
pre_right.push_back((pre[i]));
}
else{
if(pre[0]==vin[i])idx=1;
else{
vin_left.push_back(vin[i]);
pre_left.push_back(pre[i+1]);
}
}
}
TreeNode* res = new TreeNode(pre[0]);
res->left = reConstructBinaryTree(pre_left, vin_left);
res->right = reConstructBinaryTree(pre_right, vin_right);
return res;
}
2.3.1 该题的设计思路
- 基本思路
- 前序遍历:根结点左子树右子树;中序遍历:左子树根节点右子树
- 每次都从前序遍历中获得每次的根节点,然后再中序遍历中找到该位置,得到前序遍历和中序遍历的左右子树,然后再分别对左右子树进行同样的操作。
- 一直递归直到没有左右子树的时候
- 时间复杂度为O(n);
- 空间复杂度为O(n);
2.3.2 该题的伪代码
TreeNode* reConstructBinaryTree(vector<int> pre,vector<int> vin)
{
if 先序或中序为空 return null
end if
int idx=0;//
分别建立几个存放先序和中序遍历的左右子树的容器
for i=0 to 中序长度-1
if (idx)//已经找到根节点
继续把中序遍历和先序遍历剩下的分别放进属于他们的右子树中
else if 找到根节点 idx=1;
else 把中序继续放进它的左子树容器中
把先序序列则下移
end if
end if
建立一个新的根节点
然后进行左右子树递归,把容器里的左子树右子树进行递归建树
一直到没有左右子树的时候
2.3.3 运行结果
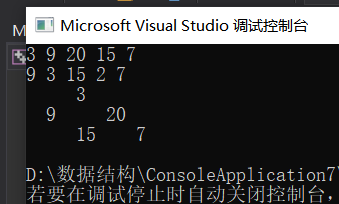
2.3.4分析该题目解题优势及难点。
- 该题的优势在于它使用了vector容器,相对比上课讲的方法,上课讲的是指针数组来进行建树,来说就更加的不容易出错,因为下标容易越界或者是段错误,而且善用idx,就是提前先弄好的容器里面的东东,最后用容器里的东东来建就好了,就更加的方便,大致思路都和课上差不多,就是觉得这个代码更加巧妙一点,更容易看懂。
- 难点在于找根的时候先序序列该怎么做,这个是要画图出来看会更加明确,更好理解的。
2.4 相同的树
🍓题目
给定两个二叉树,编写一个函数来检验它们是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例 1:
输入: 1 1
/ \ /
2 3 2 3[1,2,3], [1,2,3]输出: true
示例 2:
输入: 1 1
/
2 2[1,2], [1,null,2]输出: false
示例 3:
输入: 1 1
/ \ /
2 1 1 2[1,2,1], [1,1,2]输出: false
🍓解题代码
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
if(!p && !q) return true;
if(!p || !q) return false;
return (p->val == q->val)
&& (isSameTree(p->left,q->left)
&& isSameTree(p->right,q->right));
}
};`
2.4.1 该题的设计思路
- 基本思路:
利用递归的方法,当两指针都不为空的时候检查两者的数据域是否相等,若当前数据域相等则继续比较两者的左孩子,右孩子,若不相等返回false或者。当两指针都指向空的时候代表两者该点没有储存数值,返回true。当两者指针只有一方为空的时候,代表出现了另一方没有的节点,返回false
- 时间复杂度:O(n),n为节点数
- 空间复杂度:O(h),h为树的高度
2.4.2 该题的伪代码
bool isSameTree(TreeNode* p,TreeNode* q)
{
if(q为空且p也为空)返回true;
end if
if(p不为空或者q不为空)返回false;
end if
返回(p->val==q->val)&&(isSameTree(p->left,q->left)&&isSameTree(p->right,q->right));
}
2.4.3 运行结果
2.4.4分析该题目解题优势及难点
- 代码简洁明了,利用递归减少代码的长度,三种情况容易看得清楚,易于理解
- 这题也没什么特别难的地方,主要是递归比较难写吧
- 值得注意的是一定要小心空树的情况,不然容易崩溃
- 使用bool类型,更加方便简洁,不需要设置什么flag之类的东西,直接返回输出即可~


