DS博客作业02--栈和队列
0.PTA得分截图

1.本周学习总结
1.1 总结栈和队列内容
🧸栈
✨️ 栈的定义及其特点
- 栈的定义(如图所示):

- 栈的特点:不讲究先来后到,只讲究后进先出,先进后出
✨️ 栈的存储结构及其操作
无论是顺序栈还是链栈都少不了建栈,进栈,出栈,取栈顶元素,判断栈是否为空
🐤 顺序栈
- 定义:类比数组,栈顶就是数组的最后一个元素,只能对最后一个元素进行删除,或者在最后一个元素后面增添
typedef struct
{ ElemType data[MaxSize]; //数据域
int top; //栈顶指针
} Stack,*SqStack;
❤️顺序栈建栈:
void Stack(SqStack &s)
{ s=new Stack;
s->top=-1;//初始化栈顶的下标
}
| 类比数组 | data | data | …… | data | |
|---|---|---|---|---|---|
| 下标 | -1 | 1 | 2 | …… | MaxSize-1 |
| top | |||||
| 初始化 |
可知顺序栈判断栈空为:bool S_Empty(SqStack s) return(s->top==-1);
如果栈数据域定义时是指针,则建栈时需要申请内存才能变成变量
❤️顺序栈进栈
bool s_Push(SqStack &s,ElemType e)
{
if (s->top==MaxSize-1)
return false;//栈满情况
s->top++; //先让下标+1
s->data[s->top]=e;//再存入数据
return true;
}
| 类比数组 | e | …… | |||
|---|---|---|---|---|---|
| 下标 | -1 | 1 | 2 | …… | MaxSize-1 |
| top |
❤️顺序栈出栈
bool s_Pop(SqStack &s,ElemType &e)
{
if (s->top==-1) //栈为空的情况,不能出栈
return false;
e=s->data[s->top];//记录此时的栈顶元素
s->top--; //栈顶指针减1,直接删除
return true;
}
和数组不同的是,因为栈是指针,所以当它栈顶指针--的时候,原来的栈顶就会出栈

❤️顺序栈取栈顶元素
bool s_Top(SqStack *s,ElemType &e)
{
if (s->top==-1) //栈为空的情况
return false;
e=s->data[s->top];
return true;
}

取红色部分即栈顶元素
🐤链栈
实际上链栈就是使用头插法建立的一条链,栈顶为头节点之后的第一个节点元素
- 定义:
typedef struct linknode
{ ElemType data; //数据域
struct linknode *next; //指针域
} LiNode,*LiStack;
❤️链栈建栈(建一个头结点)
void Stack(LiStack &s)
{ s=new LiNode;
s->next=NULL;
}
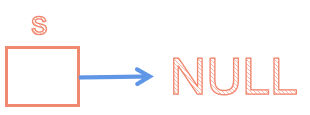
❤️链栈进栈(实际上就是头插法建链的过程)
- 进栈:
- 头插法:
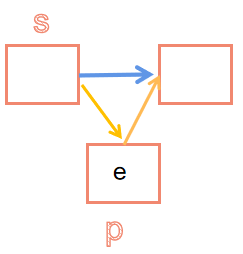
- 头插法:
void s_Push(LiStack &s,ElemType e)
{ LiStack p;
p=new LiNode;
p->data=e;
p->next=s->next;
s->next=p;
}
链栈不需要考虑栈满的情况
❤️链栈出栈
- 栈S为空的条件是s->next==NULL
- 判断栈是否为空:
bool s_Empty(LiStack s) return(s->next==NULL);- 出栈:
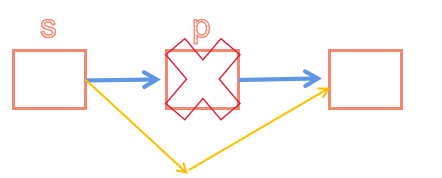
- 出栈:
bool s_Pop(LiStack &s,ElemType &e)
{ LiStack p;
if (s_Empty(s)) //栈空的情况
return false;
p=s->next; //p指向栈顶节点
e=p->data;
s->next=p->next; //跨过p
delete p; //释放
return true;
}
❤️链栈取栈顶元素
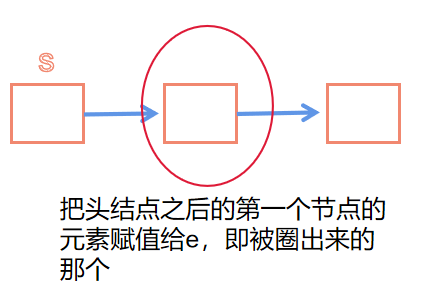
bool s_Top(LiStack s,ElemType &e)
{ if (s_Empty(s)) //栈空的情况
return false;
e=s->next->data;
return true;
}
✨️C++容器 栈
- 库:
#include <stack>- stack
s :初始化栈,参数比如int表示元素类型,s为栈的名字 - s.push(t): 入栈元素t
- s.top(): 返回栈顶元素
- s.pop(): 删除栈顶元素,并不返回该元素。
- s.empty(): 当栈空时,返回true。
- s.size(): 访问栈中的元素个数
- stack
✨️栈的运用
- 符号配对
- 表达式转换
- 迷宫求解
………………………………
例如:符号配对 - 思路:
输入一串字符串,包括[],{},()等 来进行配对,所以把左括号存进栈里,如果是右括号则进行配对,如果不配对则返回配对失败的元素,如果最后栈为空则匹配成功,否则返回栈顶元素
- 伪代码:
string str;cin>>str;
strlen=str.size();
for i=0 to strlen-1
if str[i]是左括号 则入栈
end if
if str[i]是右括号
if 栈不为空且与栈内元素匹配时
pop();
else 匹配失败记录栈顶元素返回false
end if
end if
end for
if栈不为空 那么返回栈顶元素 匹配失败
else 匹配成功 返回true
🧸队列
✨️ 队列的定义及其特点
- 队列的定义(如图所示):

- 队列的特点:讲究先来后到,具有先进先出,后进后出的特点
✨️ 队列的存储结构及其操作
🐤顺序队列和循环队列
- 定义:要有队头和队尾指针的结构
typedef struct
{ ElemType data[MaxSize]; //数据域
int front,rear; //队首和队尾指针
} Queue;
typedef Queue *SqQueue;
顺序队列容易假溢出,因为它队空的条件是rear==MaxSize-1,这时候通过更改条件可以改成循环队列修改这个缺陷
两者的结构体定义一样
❤️顺序队列和循环队列 建队
- 顺序队列
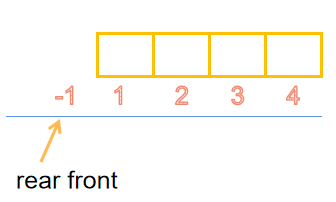
void Queue(SqQueue &q)
{
q=new Queue;
q->front=q->rear=-1;
}
- 循环队列
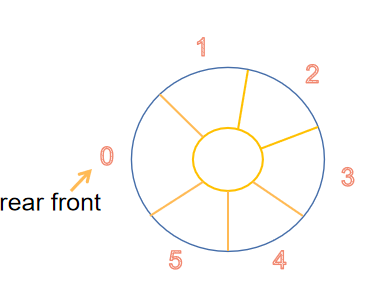
void InitQueue(SqQueue &q)
{
q=new Queue;
q->front=q->rear=0;
}
❤️顺序队列和循环队列 入队
- 顺序队列
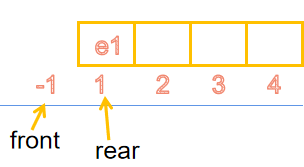
bool enQueue(SqQueue &q,ElemType e)
{
if (q->rear+1==MaxSize) return false;//队满条件
q->rear=q->rear+1;
q->data[q->rear]=e;
return true;
}
- 循环队列
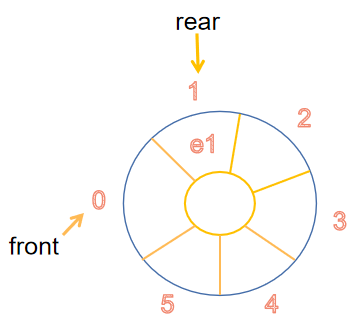
bool enQueue(SqQueue &q,ElemType e)
{
if ((q->rear+1)%MaxSize==q->front) //队满,不容易假溢出
return false;
q->rear=(q->rear+1)%MaxSize;
q->data[q->rear]=e;
return true;
}
假溢出
顺序队列的队满条件是front==rear 而循环队列是(rear+1)%MaxSize
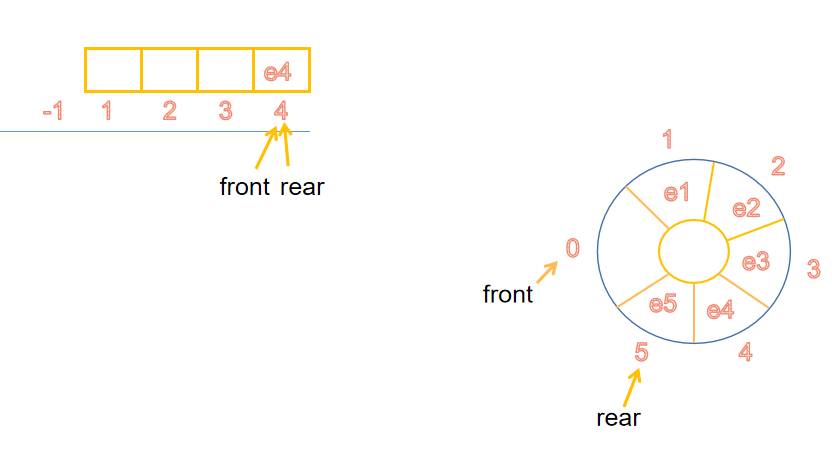
由图可知顺序队列可能会造成假溢出
❤️顺序队列和循环队列 判断队列是否为空
bool QueueEmpty(SqQueue q)
{
return(q->front==q->rear);
}
❤️顺序队列和循环队列 出队
- 顺序队列
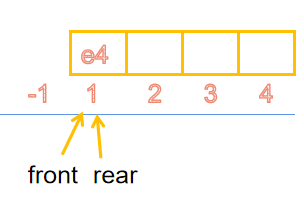
bool deQueue(SqQueue &q,ElemType &e)
{
if (q->front==q->rear) //队空
return false;
q->front=q->front+1;
e=q->data[q->front];
return true;
}
- 循环队列
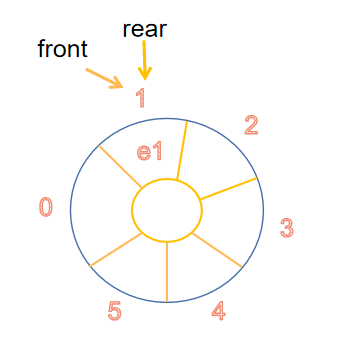
bool deQueue(SqQueue &q,ElemType &e)
{ if (q->front==q->rear) //队空
return false;
q->front=(q->front+1)%MaxSize;
e=q->data[q->front];
return true;
}
✨️C++容器 队列
- 库:
#include <queue>- queue
q1: 初始化队列 q1为队列名称 char为队列元素类型 - q.push(x): 将x接到队列的末端。
- q.pop():弹出队列的第一个元素
- q1.front():即最早被压入队列的元素。
- q1.back():即最后被压入队列的元素。
- q1.empty():当队列空时,返回true。
- q1.size():访问队列中的元素个数
- queue
✨️队列的应用
- 报数游戏
- 操作系统
- 售票系统
- 印机
- 手机短信发送
………………………………
例如:报数游戏
报数游戏其实就是入队出队一直到遇到目标元素的时候出队 然后重复操作即可
目标第m个 共有n个
初始化一个队列 然后赋值
if m>n return 0;
for i=0 to n
if i==m
cout << q.top()
q.pop();
else
q.push(q.top());
q.pop();
end if
end for
1.2.谈谈你对栈和队列的认识及学习体会。
栈和队列其实还是很好理解的,比链表要舒服很多,但是具体理解还是要靠画图思考,也别是更深层的问题,要考虑栈和队列用哪一个或者是不是都用,而且像迷宫求解,银行排队这些题目都是综合性比较高的题目,如果不多练就没办法做好,总之还是再接再厉把。加油!
2.PTA实验作业
2.1 编程题:7-5 表达式转换
🧸题目:
算术表达式有前缀表示法、中缀表示法和后缀表示法等形式。日常使用的算术表达式是采用中缀表示法,即二元运算符位于两个运算数中间。请设计程序将中缀表达式转换为后缀表达式。
输入格式:
输入在一行中给出不含空格的中缀表达式,可包含
+、-、*、\以及左右括号(),表达式不超过20个字符。输出格式:
在一行中输出转换后的后缀表达式,要求不同对象(运算数、运算符号)之间以空格分隔,但结尾不得有多余空格。
输入样例:
2+3*(7-4)+8/4输出样例:
2 3 7 4 - * + 8 4 / + ``
2.1.1 代码截图


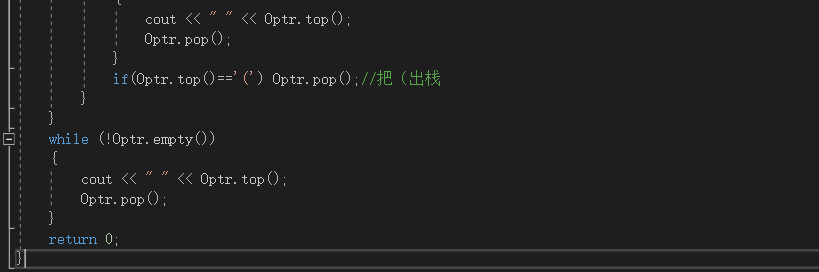
2.1.2本题PTA提交列表说明
问题及解决方法
这道题一开始就是各种错误,什么段错误啊什么格式错误啊,我一开始是用一个字符数组来储存后缀表达式的,导致格式很容易出错,同时也没有考虑到正负号的时候以及小数或者大于9的数的时候,后来为了改成格式错误,我改成了边判断边输出,然后利用变量来判断正负号,把错误改过来基本就没事了,具体错误点我在代码的注释里写了,值得注意的是在if的判断力 如果要判断栈为空,且有两个条件时,判断栈是否为空写在第一个条件上,其次还要考虑嵌套括号等情况,然后改正即可
2.2 编程题:7-7 银行业务队列简单模拟
🧸题目:
设某银行有A、B两个业务窗口,且处理业务的速度不一样,其中A窗口处理速度是B窗口的2倍 —— 即当A窗口每处理完2个顾客时,B窗口处理完1个顾客。给定到达银行的顾客序列,请按业务完成的顺序输出顾客序列。假定不考虑顾客先后到达的时间间隔,并且当不同窗口同时处理完2个顾客时,A窗口顾客优先输出。
输入格式:
输入为一行正整数,其中第1个数字N(≤1000)为顾客总数,后面跟着N位顾客的编号。编号为奇数的顾客需要到A窗口办理业务,为偶数的顾客则去B窗口。数字间以空格分隔。
输出格式:
按业务处理完成的顺序输出顾客的编号。数字间以空格分隔,但最后一个编号后不能有多余的空格。
输入样例:
8 2 1 3 9 4 11 13 15输出样例:
1 3 2 9 11 4 13 15
2.2.1 代码截图
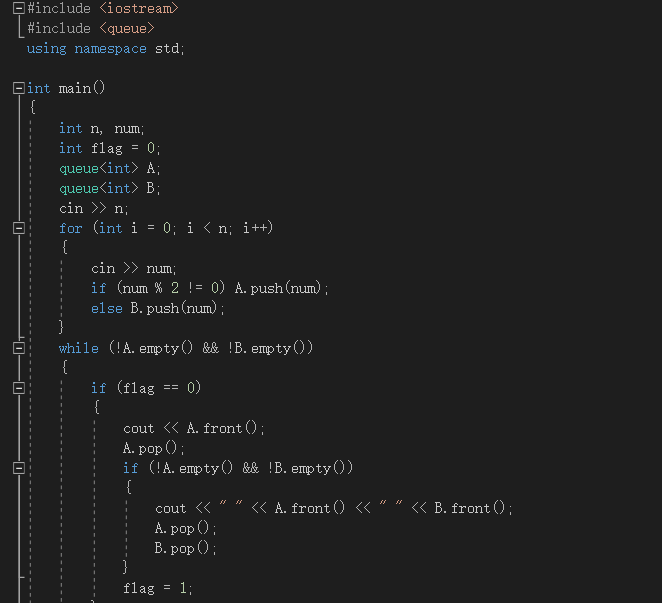
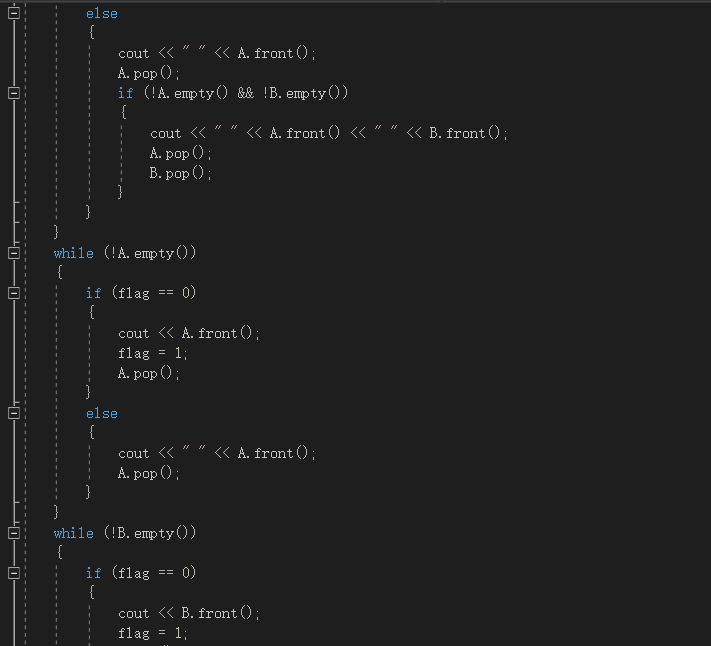

2.2.2本题PTA提交列表说明

问题及解决方法
我这里的问题就是一开始没有理解速度的两倍,就只是单纯的输出两个A窗口的客户的时候只输出一个B窗口的客户 没有考虑到如果A窗口是一个客户B窗口也是一个客户的时候怎么办,所以要对他进行栈的非空判断,因为非空判断是最容易出错的地方,容易错误
3.阅读代码
3.1 题目及其解题代码
🧸题目:验证栈序列
本题来自力扣
给定 pushed 和 popped 两个序列,每个序列中的 值都不重复,只有当它们可能是在最初空栈上进行的推入 push 和弹出 pop 操作序列的结果时,返回 true;否则,返回 false 。
示例 1:
输入:pushed = [1,2,3,4,5], popped = [4,5,3,2,1]
输出:true
解释:我们可以按以下顺序执行:
push(1), push(2), push(3), push(4), pop() -> 4,
push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1示例 2:
输入:pushed = [1,2,3,4,5], popped = [4,3,5,1,2]
输出:false
解释:1 不能在 2 之前弹出。提示:
0 <= pushed.length == popped.length <= 1000
0 <= pushed[i], popped[i] < 1000
pushed 是 popped 的排列。
🧸解题代码
class Solution {
public:
bool validateStackSequences(vector<int>& pushed, vector<int>& popped) {
stack<int > a;
int sizePush=pushed.size();
int sizePop=popped.size();
int sizePush1=0;
int sizePop1=0;
while (sizePush1<sizePush&&sizePop1<sizePop){
a.push(pushed[sizePush1]);
while(!a.empty()&&a.top()==popped[sizePop1]){//查看是否可以出栈
a.pop();
sizePop1++;
}
sizePush1++;
}
return a.empty();
}
};
3.1.1 该题的设计思路
- 构建一个栈,来模拟出栈入栈的顺序,从而判断是否返回true,让入栈序列一个一个入栈判断,如果栈顶等于出栈序列的元素,则意味着栈顶要出栈,不满足就继续压栈,一直比到最后直到栈为空的时候就是配对成功,否则失败。




- 时间复杂度:O(N),其中 N 是 pushed 序列和 popped 序列的长度。
- 空间复杂度:O(N).
3.1.2 该题的伪代码
stack<int> a//建立一个栈用来模拟出栈入栈
用sizePush和sizePop来记录两个序列的长度
然后用sizePush1和sizePop1来作为两个序列的下标
while(两个序列的下标都小许序列长度-1)
让pushed[sizePush1]入栈
while(栈顶不为空且栈顶等于popped[sizepop1])
出栈 然后sizepop1++ //popped数组下移
end while
sizePush1++;不满足或者匹配成功都要继续压栈
end while
return a.empty();
3.1.3 运行结果
3.1.4分析该题目解题优势及难点。
主要是模拟出栈入栈的过程,这里利用两个序列的下标然后让序列的单独入栈与出栈序列作比较,下移,过程简单,容易理解,而且利用栈是否为空就可以判断该返回的是true还是false,我觉得很妙啊。但是容易出错的是什么时候压栈,有时候容易误以为压栈只有匹配不成功的时候压栈,如果匹配成功也需要压栈,同时在匹配之前一定要记得判断栈是不是为空
3.2 题目及其解题代码
🧸题目:根据身高重建队列
本题来自力扣
假设有打乱顺序的一群人站成一个队列。 每个人由一个整数对(h, k)表示,其中h是这个人的身高,k是排在这个人前面且身高大于或等于h的人数。 编写一个算法来重建这个队列。
注意:
总人数少于1100人。示例
输入:
[[7,0], [4,4], [7,1], [5,0], [6,1], [5,2]]输出:
[[5,0], [7,0], [5,2], [6,1], [4,4], [7,1]]
🧸解题代码
class Solution {
public:
vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
// 排序
sort(people.begin(), people.end(),
[](const vector<int>& lhs, const vector<int>& rhs)
{return lhs[0] == rhs[0] ? lhs[1] <= rhs[1] : lhs[0] > rhs[0];});
int len = people.size();
list<vector<int>> tmp;
// 循环插入
for(int i = 0; i < len; ++i){
auto pos = tmp.begin();
advance(pos, people[i][1]);
tmp.insert(pos, people[i]);
}
// 重建vector返回
return vector<vector<int>>(tmp.begin(), tmp.end());
}
};
3.2.1 该题的设计思路
先介绍几个操作才能看懂这串代码
- insert()操作
- 列表 insert() 方法将指定对象插入到列表中的指定位置。
L.insert(index,obj); //index -- 对象obj需要插入的索引值。obj -- 要插入列表中的对象。 - 该方法没有返回值,但会在列表指定位置插入指定对象。
- advance()用来寻找插入位置;sort()用来插入排序
- list作为insert()的中间容器
- vector是向量类型,可以容纳许多类型的数据,因此也被称为容器,将完成所有插入操作的list重建为vector返回。
- 列表 insert() 方法将指定对象插入到列表中的指定位置。
- 思路
先将people按照身高降序排序,又由于每次插入的位置是k,所以相同身高需要按k升序排序,否则插入位置会越界
- 时间复杂度:O(n)。都是只需要一次循环
- 空间复杂度:O(n)。
3.2.2 该题的伪代码
利用sort()将people按照身高降序排序
相同身高需要按k升序
len用来存储人数
新建list容器tmp临时存放people中的数据
for i=0 to len-1
寻找并将数据插入对应位置
end for
返回 tmp重建的vector容器
3.2.3 运行结果
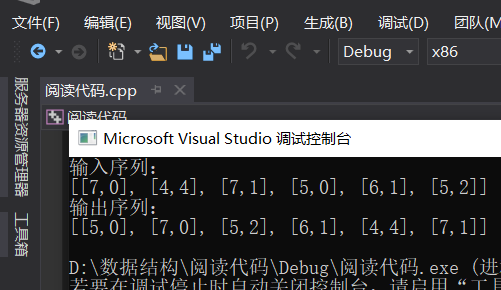
3.2.4分析该题目解题优势及难点
代码量简短,效率高,使用list作为中间容器而不直接使用vectot,大大提高了运行效率。
但使用的函数和操作复杂,需要课外拓展,需要借助各种头文件。
在排身高的时候要考虑越界等问题

