201871010123-吴丽丽 实验二 个人项目——处理背包问题
| 项目 | 内容 |
|---|---|
| 课堂班级博客链接 | 班级博客 |
| 这个作业要求链接 | 作业要求 |
| 我的课程学习目标 | 1.自己动手做项目,从而了解如何去开发项目,掌握软件项目个人开发的流程 2.能够用Github发布软件项目 3.掌握动态规划算法、回溯算法 |
| 这个作业在哪些方面帮助我实现学习目标 | 1.通过阅读《构建之法》来掌握PSP流程 2.自己动手操作,掌握用Github发布软件项目的技巧 3.通过网上查找资料来自主学习,从而对背包问题、动态规划算法、回溯算法有自己的认识 |
| 项目Github的仓库链接地址 |
一、实验目的与要求
(1)掌握软件项目个人开发流程。
(2)掌握Github发布软件项目的操作方法。
二、实验内容和步骤
任务1:阅读教师博客“常用源代码管理工具与开发工具”内容要求,点评班级博客中已提交相关至少3份作业。
任务2:详细阅读《构建之法》第1章、第2章,掌握PSP流程
已经阅读《构建之法》第1章、第2章内容,以下是通过阅读书籍,认为比较重要的几个概念:
1.软件=程序+软件工程 软件企业=软件+商业模式
2.软件工程是把系统的、有序的、可量化的方法应用到软件的开发、运营和维护上的过程。
3.软件工程包括软件需求分析、软件设计、软件构建、软件测试和软件维护。
4.软件是可以运行在计算机及电子设备中的指令和数据的有序集合。软件有各种分类方法,其中一种分为:系统软件、应用软件、恶意软件。
5.软件的基本特性有:
- 复杂性
- 不可见性
- 易变性
- 服从性
- 非连续性
6.PSP流程
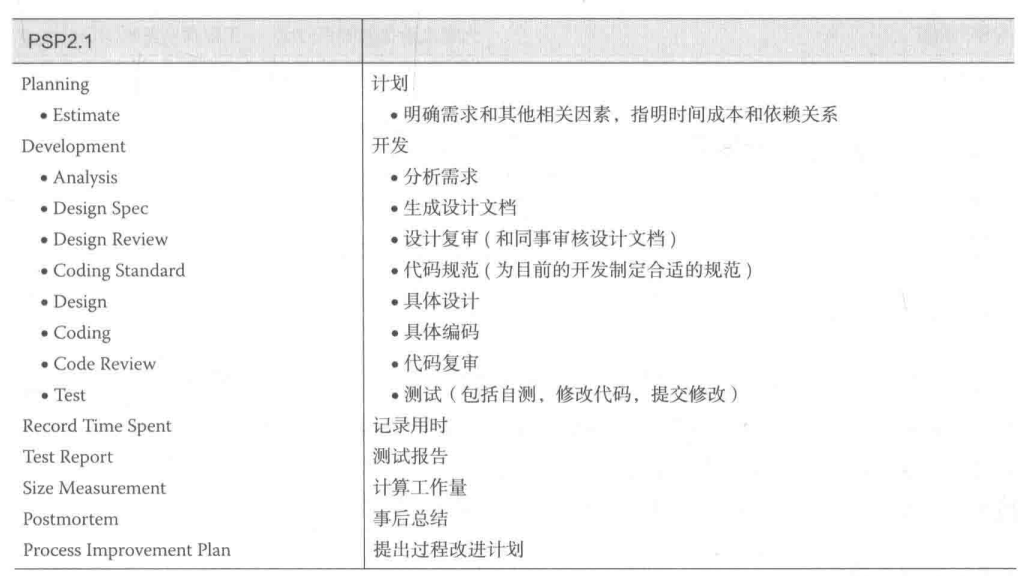
任务3:项目开发
1.项目开发背景:背包问题(Knapsack Problem,KP)是NP Complete问题,也是一个经典的组合优化问题,有着广泛而重要的应用背景。{0-1}背包问题({0-1 }Knapsack Problem,{0-1}KP)是最基本的KP问题形式,它的一般描述为:从若干具有价值系数与重量系数的物品(或项)中,选择若干个装入一个具有载重限制的背包,如何选择才能使装入物品的重量系数之和在不超过背包载重前提下价值系数之和达到最大?
2.开发要求:
D{0-1} KP 是经典{ 0-1}背包问题的一个拓展形式,用以对实际商业活动中折扣销售、捆绑销售等现象进行最优化求解,达到获利最大化。D{0-1}KP数据集由一组项集组成,每个项集有3项物品可供背包装入选择,其中第三项价值是前两项之和,第三项的重量小于其他两项之和,算法求解过程中,如果选择了某个项集,则需要确定选择项集的哪个物品,每个项集的三个项中至多有一个可以被选择装入背包,D{0-1} KP问题要求计算在不超过背包载重量 的条件下,从给定的一组项集中选择满足要求装入背包的项,使得装入背包所有项的价值系数之和达到最大;D{0-1}KP instances数据集是研究D{0-1}背包问题时,用于评测和观察设计算法性能的标准数据集;动态规划算法、回溯算法是求解D{0-1}背包问题的经典算法。查阅相关资料,设计一个采用动态规划算法、回溯算法求解D{0-1}背包问题的程序,程序基本功能要求如下:
a.可正确读入实验数据文件的有效D{0-1}KP数据;
b.能够绘制任意一组D{0-1}KP数据以重量为横轴、价值为纵轴的数据散点图;
c. 能够对一组D{0-1}KP数据按项集第三项的价值:重量比进行非递增排序;
d.用户能够自主选择动态规划算法、回溯算法求解指定D{0-1} KP数据的最优解和求解时间(以秒为单位);
e.任意一组D{0-1} KP数据的最优解、求解时间和解向量可保存为txt文件或导出EXCEL文件。
3.需求分析
-
背包问题是一个经典的组合问题,{0-1}背包问题是最基本的KP问题形式,其特点是:每种物品只有一件,可以选择放或者不放。如:有n种物品,物品j的重量为wj,价格为pj,假定所有物品的重量和价格都是非负的,背包所能承受的最大重量为W,可以用公式表示为:最大化
 受限于
受限于 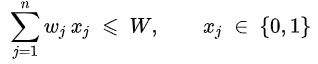
-
D{0-1}是经典{0-1}背包问题的拓展形式,动态规划算法、回溯算法是求解D{0-1}背包问题的经典算法。其中动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中,可能会有许多可行解。每一个解都对应于一个值,我们希望找到具有最优值的解。其基本思想是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解,因经分解得到子问题往往不是互相独立的,所以我们可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到,只要它被计算过,就将其结果填入表中。这就是动态规划法的基本思路。而回溯算法实际上一个类似枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回,尝试别的路径。回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法。其基本思想是:从一条路往前走,能进则进,不能进则退回来,换一条路再试。
-
通过分析,我们要能够将数据正确的读入,制作相应的散点图,对价值进行排序,采用动态规划算法、回溯算法来进行求解,能够以文件的形式呈现出结果,这些功能我们都将从函数来入手,让函数执行相应的功能。
4.功能设计
- 基本功能:
- 可正确读入实验数据文件的有效D{0-1}KP数据;
- 能够绘制任意一组D{0-1}KP数据以重量为横轴、价值为纵轴的数据散点图;
- 能够对一组D{0-1}KP数据按项集第三项的价值:重量比进行非递增排序;
- 用户能够自主选择动态规划算法、回溯算法求解指定D{0-1} KP数据的最优解和求解时间(以秒为单位);
- 任意一组D{0-1}KP数据的最优解、求解时间和解向量可保存为txt文件或导出EXCEL文件。
- 扩展功能:
- 能够以直方图的形式来进行比较用两种不同算法的求解时间
- 能够让用户简洁明了的进行操作,不必苦恼于如何使用,让其有一个好的用户体验
5.设计实现
- 在本次项目中计划着采用Python来写,用列表来存储相关数据,设置一个函数来进行读取文件,将数据进行相应的处理,再通过一个绘制函数来绘制以重量为横轴、价值为纵轴的数据散点图,设置一个排序函数来进行排序,再设计动态规划算法函数、回溯算法函数来求解指定D{0-1}数据的最优解,设计一个计算求解的时间函数来进行计算求解的时间,最后能够设置一个保存的函数来以txt、excel文件来保存对应的数据。最后通过设计主函数,有多个选项让用户选择,选择相应的选项,会做出对应的反应。
6.测试运行
读取数据:

绘制数据散点图:
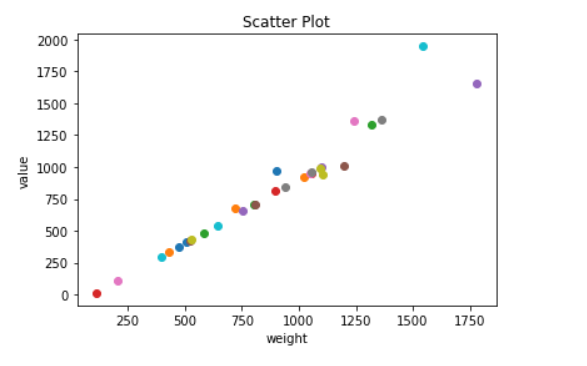
对IDKP0中第三项价值:重量进行排序:

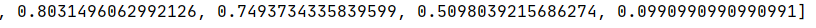
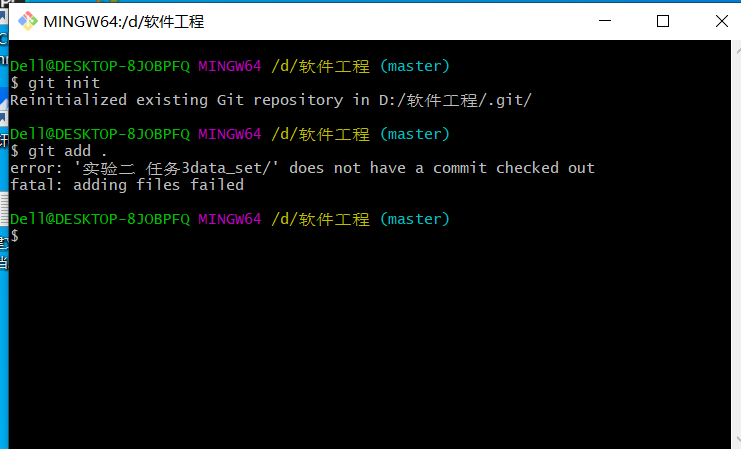
上传项目,创建仓库不成功:
用动态规划算法运行IDKP0数据得到的最大价值和运行时间,其运行截图如下:

7.代码展示
读取数据:
with open('idkp1-10.txt') as f:
allstr = f.readlines()
#print(allstr)
def func(s):
for i in range(len(allstr)):
if s in allstr[i]:
v1,v2 = allstr[i+1].split(',')
n=v1.split('=')[-1]
c=v2.split()[-1][:-1]
print('diemnsion: ',n)
print('cubage: ',c)
p = allstr[i+3].split(',')
print("物品的价值为:",p[:-1])
w = allstr[i+5].split(',')
print("物品的重量为:",w[:-1])
func('IDKP0')
绘制散点图:
def draw_scatter(n,v,w):
x=[]
y=[]
W=[]
V=[]
for i in range(n):
x=int(w[i])
W.append(x)
y=int(v[i])
v.append(y)
plt.scatter(x,y)
plt.title("W-V scatter plot")
plt.xlabel("W")
plt.ylabel("V")
plt.show()
排序算法:
def datasorted(w,v):
v_w=[]
v1=v[2::3]
w1=w[2::3]
for i in range(len(v1)):
s=int(v[i])/int(w[i])
v_w.append(s)
v_w.sort(reverse=True)
print(v_w)
动态规划算法:
def pack(w,v,C):
"""
w:list[list,list,...]
v:list[list,list,...]
"""
begin=time.time()
n_list = [3, 3, 3, 3, 3, 3, 3, 3, 3, 3]
dp = [0 for _ in range(C + 1)]
for i in range(1, len(w) + 1): # 物品循环
for j in reversed(range(1, C + 1)): # 剩余体积循环
for k in range(n_list[i - 1]): # 别的和0,1背包一样 就是这里枚举一下每个组内的值,在每个组内选出一个max值
if j - w[i - 1][k] >= 0:
dp[j] = max(dp[j], dp[j - w[i - 1][k]] + v[i - 1][k])
print("最大的价值为:",dp[C])
end=time.time()
print("运行时间为:",end-begin)
8.总结
- 在本次作业中,自己并没有能够按时的完成项目,因自己的编程能力有限,能实现的功能比较少,所以对于本次的个人项目无法完成。我觉得老师在安排项目的时候能够从学生本身的能力出发,虽然我们之前已经学习过相关的内容,但是对于项目的开发还是有一定的难度。
9.展示PSP
| PSP | 任务内容 | 计划共完成需要的时间(h) | 实际完成需要的时间(h) |
|---|---|---|---|
| Estimate | 估计这个任务需要多少时间,并规划大致工作步骤 | 1 | 0.8 |
| Development | 开发 | 48 | - |
| Analysis | 需求分析 (包括学习新技术) | 5 | 6 |
| Design Spec | 生成设计文档 | 3 | 2 |
| Design Review | 设计复审 (和同事审核设计文档) | 0 | 0 |
| Coding Standard | 代码规范 (为目前的开发制定合适的规范) | 1 | 2 |
| Design | 具体设计 | 10 | - |
| Coding | 具体编码 | 20 | - |
| Code Review | 代码复审 | 2 | - |
| Test | 测试(自我测试,修改代码,提交修改) | 1 | - |
| Reporting | 报告 | 1 | - |
| Test Report | 测试报告 | 2 | - |
| Size Measurement | 计算工作量 | 2 | - |
| Postmortem & Process Improvement Plan | 事后总结 ,并提出过程改进计划 | 1 | - |



