一些好玩的Hash算法(CMU15445)
Hash策略的分类
静态哈希
哈希表底层实际是一个数组嘛,静态哈希就是一个槽位一个值,当碰撞发生会采用某种机制占用其它的槽位。
那么假设当前槽位数为N,就只能存N个元素,如果想要保存更多元素,需要创建新的底层数组,对Hash表上的全部元素重新使用新的Hash函数进行迁移。
典型的静态哈希算法就是上课都学过的线性探测法(也叫开放寻址法)。
所以使用静态哈希的前提是你能够较为准确的预估要保存的键值对的数量,然后你提供更多个槽位,避免哈希表迁移。但在数据库系统中,我们经常使用Hash表来做Join之类的工作,在Join之前,我们很难预估具体的数量。
动态哈希
为了避免静态哈希的迁移,动态哈希策略允许哈希表中存储大于槽位个键值对。
若当前槽位数为N,动态哈希策略允许保存多于N个元素 。
最简单的就是链表法嘛(但是数据库系统中的稍有些差别),动态哈希算法通常还要考虑在元素数量不断增加时如何渐进式的改动整个Hash表,从而让性能不会退化的太严重(考虑链表法性能会下降到O(N))
Chained Hashing
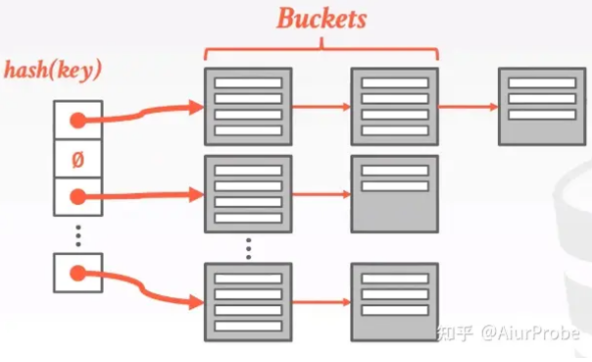
实际上和链表法是一样的。
首先我们有N个槽位,每一个槽位指向一个链表,这样我们便可以无限的向N个槽的HashTable添加更多的内容。
有一个区别,在数据库系统中应用的HashTable,通常都会有Bucket的概念,比如这里槽中保存的实际上是一个Bucket的链表。
Bucket中有多条键值对数据,正常来说它应该是一个数据库页的大小,我想这样做的原因有两个:
- 更利好磁盘,每次从磁盘读20字节挺蠢的
- 利好CPU的CacheLine,因为相邻的数据被放置在Bucket中,CPU一次性预取到缓存内。考虑Bucket大小为一个键值对(也就是单纯的链表),那么遍历是随机的,每一个键值对都要访问一次内存
链地址法的问题挺明显的,就是它虽然允许无限存放数据,但当数据量M与N的差值越大,对HashTable的访问性能趋近于链表。
实际上可以将Bucket链表组织成树以加速查找,但是教授指出实际的商用系统里可能还是更偏向直接使用简单的链表
若想让HashTable的访问性能恢复,实际上你还得重建整个HashTable,对每一个元素进行重映射,而这正与我们使用动态策略的目标相悖。所以,后面的这些策略非常精妙,它们都允许渐进式的对Hash表进行扩展,并且避免在扩展时进行全局的重映射。
Extendiable Hashing
我这里斗胆来描述一下这个策略。
- 我们有一个全局变量
G,Hash表有2^G个槽位 - 每个槽位指向一个Bucket,Bucket有一个局部变量
L - 我们使用
hash(key)的前G位来确定一个key所在的槽位 - 该槽位指向的Bucket中,若对其key进行
hash(key),得到的结果前L位都是相同的 - 我们假设一个Bucket能存3条数据
- 这里你脑子里需要注意的是,我们为了方便你观察,将Bucket中的entry写成了key的hash,实际上这里存的是实际的key-value数据,稍后在对一个Bucket中的元素进行转移时,我们必须将所有的key都重新做
hash(key)运算。这种Bucket级别的迁移要比整表迁移好多了。
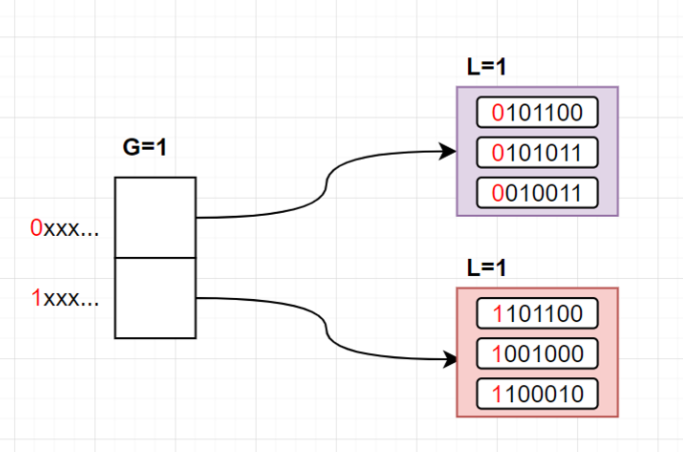
现在执行 insert(k), hash(k) = 1001110 ,明显,它要定位到第二个槽位,此时第二个槽位指向的Bucket已经满了。
此时如果我们加大前缀判断的位数,我们就可以将这个Bucket拆散,其中第一条,第三条中第二位为1,它们会分到一个Bucket中,第二条和新插入的数据第二位为0,它们会被分到一个Bucket中。
但由于 L==G ,L已经达到G的大小,G也必须跟着扩大,L和G都等于2,所以Hash表会被扩容成这样:
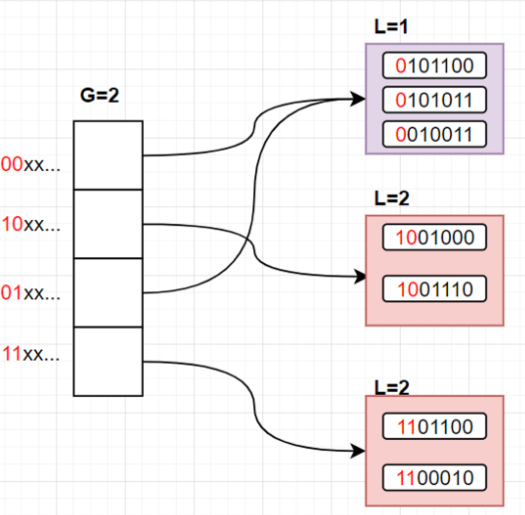
- 原来的溢出Bucket被拆分成了两个,并且L都增加了
- Hash表的槽位也被扩容了,但实际上只是对数组的简单复制,并不涉及到对所有key的rehash
- 未溢出的Bucket没动,00开头的和01开头的槽位都指向它,而它的
L==1,满足前1位相等的要求,前一位都是0
考虑此时插入 hash(k)=0100101 ,那么第一个Bucket会发生溢出,由于 L<G ,说明有多个槽位指向该Bucket,那么不用扩容数组。
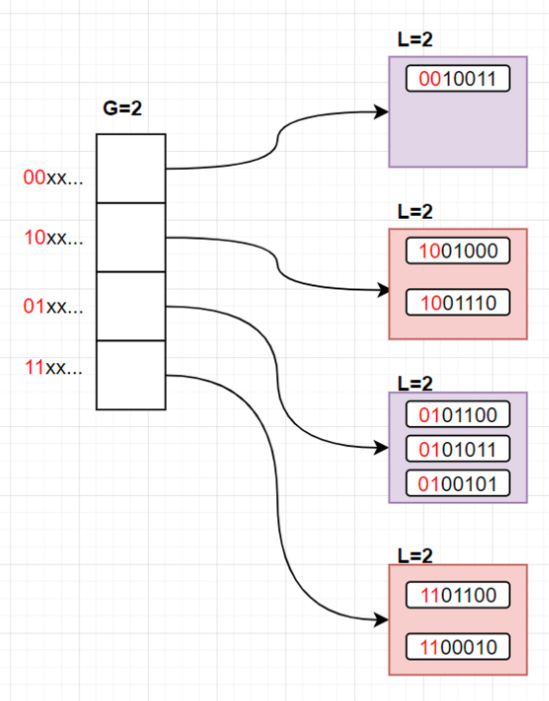
考虑若再次插入 hash(k)=0110001 ,此时第三个Bucket又将溢出,而 L==G ,再次对数组扩容:
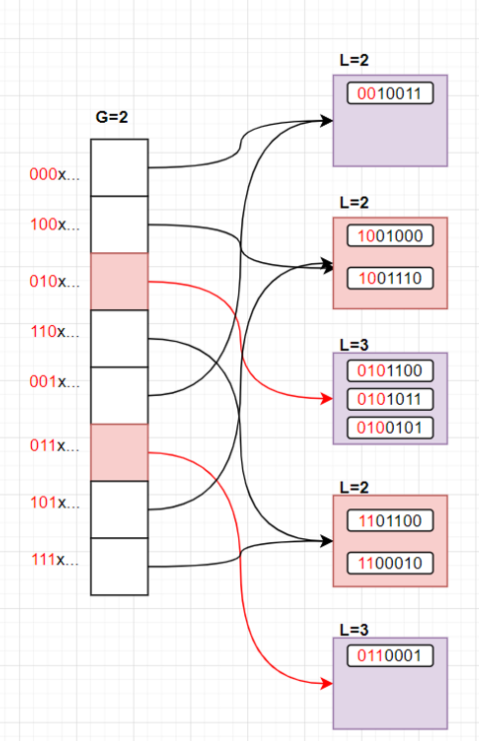
我们发现我们进行重映射的还是只有两个Bucket(我们把对应的Bucket和指向它们的指针标成了红色),其它坑位的性质不受任何影响
Extendiable Hashing让我们可以扩大底层数组的规模而不用重映射所有的元素,只重映射一个Bucket即可。
但其缺点也是每次扩大底层数组时要以2倍的形式扩充,并且要对底层数组做修复(将指针指向正确的Bucket),在修复完成前,该数据结构必须被latch锁住以防并发错误。
Linear Hashing
Linear Hashing的思路是这样的:
- 维护一个split指针,初始时它指向第0个槽位,当出现溢出Bucket,不管哪个溢出,都要拆分split指针指向的那个Bucket
- 拆分后,下移split指针一个格子,若还存在溢出Bucket,继续执行1
- 否则,扩容完成
如下图,最开始,split指针指向0,并且现在没有任何溢出Bucket,Hash表一切正常
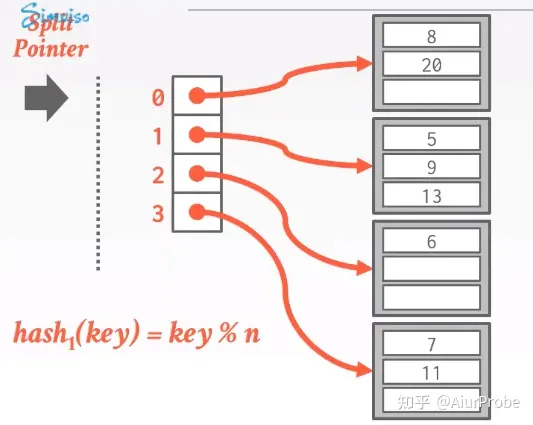
我们假设Hash键是整数,hash(key) = key % n,此时插入17,它要被插入到槽位1的Bucket中,此时发生溢出,在后面链式添加一个Bucket
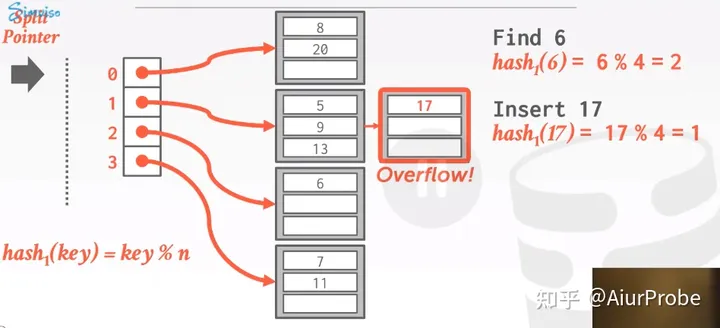
因为发生了溢出,所以开始扩容阶段,首先对split指针指向的槽位进行扩容,这里是0。新增一个槽位:
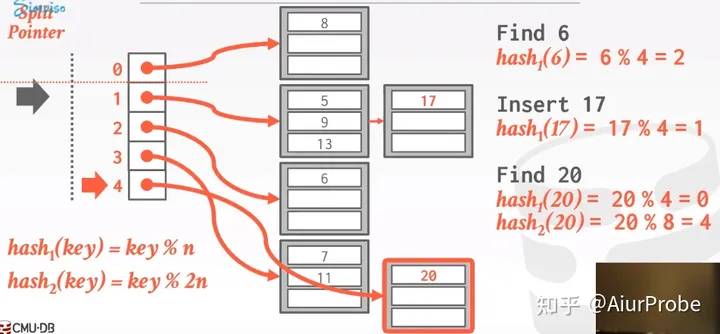
此时我们并不会将n变为5,n还是4,在最大槽位号扩大到2n之前,我们都可以用两个Hash函数对Bucket进行拆分,一个是hash1(k) = k % n,一个是hash2(k) = k % 2n。
在对一个Bucket进行拆分时,使用hash2对key进行计算会出现两种结果:
- 它还在原位置上
- 它在原位置+n的位置上
实际上貌似Java中的HashMap函数也使用了这种方式进行扩容
对split位置的元素扩容完成后,split下移。此时溢出Bucket仍然存在,还需要继续将split处(此时的1)的Bucket继续按照上面的方式拆分,也就是多了个槽位号为5的槽,并且,5、9、13、17被分配到这两个槽中。
我也不明白如果这四个数在使用hash2计算后还都处于原位时咋办,是继续扩容,直到n翻倍为2n,然后更新n为2n,继续向下扩容,祈祷下一轮时能把它们打散嘛?
当底层数组处于一个非2^k个槽的状态时,需要用两个hash函数进行查找:
- 先使用hash1运算,若得到的结果在split指针上方时,说明此时的依据是hash2函数,需要用hash2运算
- 否则使用hash1运算
该方法可以在删除一个元素时进行缩容不过我也不知道怎么缩
其实最开始认为这个算法挺鸡肋,因为每次扩容操作实际上都是申请个新数组,把原数组全部挪过去嘛,感觉没有Extendiable Hashing实用,但后来想想,为什么我们必须用一个数组呢?我们完全可以准备两个数组,一个保存n以下的那些槽,一个保存n之上的那些,只有当数组扩容到2n的长度时,我们再来两个一样长度的数组或者一个更长的数组,或者是进行一次实际的扩容。


