Rust In Action 五 Data in depth

Rust In Action 第五章翻译

这一章包含

• 学习计算机如何表示数据
• 构建一个可以工作的CPU模拟器
• 创建你自己的数字类型
• 理解浮点数

这一章完全是关于理解0与1是如何构成像文本、图片以及声音这样的大型对象的，我们也将了解计算机如何进行计算。

在这一章的末尾，我们将模拟一个功能完备的，具有CPU、内存以及用户定义方法的计算机，你将分解浮点数以构建一个你自己的，只占用一字节的数字类型。这一章还会引入一些术语，比如字节顺序（endianness）以及整数溢出（integer overflow），这些术语对于并没有做过系统编程的程序员来说可能不太熟悉。

位模式以及类型

一个小而重要的事是——一个位模式（在不同情况下）可能代表不同的东西，像Rust这样的高级语言的类型系统只是对现实世界的人工抽象，在你开始挖掘这些抽象之下的东西，并且想要得到对计算机如何运行的更深层次的理解之前，知道这件事是很有必要的。

Listing 5.1 (ch5-int-vs-int.rs)是一个使用相同的位模式来表示两种不同数字类型的例子，区分这些位模式的类型的工作是由类型系统（并不是CPU）来做的。下面展示了listing的输出：

a: 1100001111000011 50115
b: 1100001111000011 -15421

// LISTING 5.1
fn main() {
    let a: u16 = 50115;
    let b: i16 = -15421;

    // 这两个值具有相同的位模式 但它们类型不同
    println!("a: {:016b} {}", a, a);
    println!("b: {:016b} {}", b, b);
}

在位字符串和数字之间的不同映射解释了二进制文件和文本文件之间的部分区别。文本文件仅仅是遵循了在位字符串以及字符之间的某种一致的映射的二进制文件，这一种映射就称为一个编码。Arbitrary files don’t describe their meaning to the outside world, which makes these opaque.

我们可以更深一步，当我们让Rust将一个类型产生的位模式当成另一种类型使用时，会发生什么？下面的listing提供了一个答案。

// Listing 5.2
fn main() {
    let a: f32 = 42.42;

    let frankentype: u32 = unsafe {
        std::mem::transmute(a)
    };
    // 将f32类型的42.42的位串按小数查看
    println!("{}", frankentype);
    // {:032b}代表以32位通过std::fmt::Binary trait来格式化，左面补0
    println!("{:032b}", frankentype);

    let b: f32 = unsafe {
        std::mem::transmute(frankentype)
    };
    println!("{}", b);
    // 确定操作是对称的
    assert_eq!(a, b); 
}

编译并运行，Listing 5.2中的代码产生了如下输出：

1110027796
01000010001010011010111000010100
42.42

mem::transmute()方法告诉rust将f32解释成一个u32，但不修改任何底层位。

在程序中（像如上那样）混用数据类型容易造成混乱，所以我们需要在unsafe块中包裹这些操作。unsafe告诉Rust编译器，“别动，我会自己小心的”，这是你给编译器的一个信号，你告诉它你具有比它更多的上下文来验证程序的正确性。

使用unsafe关键字并不意味着（其内部的）代码就是不安全的了。举个例子，它并不允许你忽视rust的借用检查，它只是指出了编译器无法靠自己来保证程序的内存正确性。使用unsafe意味着程序员具有必须保证程序的完好的责任。

警告： 一些允许在unsafe块中使用的功能可能比其它的更加难以验证。比如，std::mem::transmute()方法就是语言中最不安全的方法之一，它打破了所有的类型安全。在你使用之前，请确认是否有其它的替代办法。

在Rust社区中，不必要的使用unsafe块是非常不推荐的，这可能让你的软件暴露在严重的安全风险下。它的主要目的是允许Rust与外部代码交互，例如一些使用其它语言编写的库以及OS接口。比起其它项目来说，这本书会经常使用unsafe块，这是因为我们的代码只是教学的工具，而不是工业软件。unsafe允许你查看和修改独立的字节，这是那些想去理解计算机如何工作的人的基础知识。

整数的一生

在前面的章节中，我们花了一些时间来讨论i32、u8或usize这些整数类型的意义。整数就像小巧精妙的鱼，它们完美的完成它们该做的，但是如果将它们带离它们的自然水域（range 范围），它们很快就会去世。

整数具有固定的范围（range）。每一个整数类型，当我们在计算机中表示它们时，它们都占用一个固定的位数。不像浮点数，整数不能牺牲它们的精度去扩展它们的范围。一旦这些位已经被填满1，唯一的前进方向就是所有位都回到0。

一个16位的整数可以表示0~65535（不包含）这些数字，当你想加到65536时会发生什么？我们来试试。

我们需要研究的这类技术术语称作——整数溢出（integer overflow）。溢出整数的一个方式是一直递增。

// Listing 5.3
fn main() {
    let mut i: u16 = 0;
    print!("{}..", i);
    loop {
        i += 1000;
        print!("{}..", i);
        if i % 10000 == 0 {
            println!("");
        }
    }
}

当我们尝试运行listing 5.3，我们的程序并没有正常的结束，让我们来看下输出：

0..1000..2000..3000..4000..5000..6000..7000..8000..9000..10000..
11000..12000..13000..14000..15000..16000..17000..18000..19000..20000..
21000..22000..23000..24000..25000..26000..27000..28000..29000..30000..
31000..32000..33000..34000..35000..36000..37000..38000..39000..40000..
41000..42000..43000..44000..45000..46000..47000..48000..49000..50000..
51000..52000..53000..54000..55000..56000..57000..58000..59000..60000..
thread 'main' panicked at 'attempt to add with overflow', examples/integer_overflow.rs:6:9
stack backtrace:
    ... omit some lines ...
note: Some details are omitted, run with `RUST_BACKTRACE=full` for a verbose backtrace.
61000..62000..63000..64000..65000..
Process finished with exit code 101

一个panic了的程序是一个死程序（dead program 也许是说是一个错误的程序），panic意味着程序员让程序做了一些做不到的事，程序不知道该怎么处理，于是它把自己关掉了。

为了了解为什么这是一类严重的bug，让我们看看底层发生了什么。Listing 5.4（ch5/ch5-bit-patterns.rs）打印了以位模式字面量形式定义的六个数字。

// Listing 5.4
fn main() {
    let zero: u16 = 0b0000_0000_0000_0000;
    let one: u16 = 0b0000_0000_0000_0001;
    let two: u16 = 0b0000_0000_0000_0010;
    // ...
    let sixtyfivethousand_533: u16 = 0b1111_1111_1111_1101;
    let sixtyfivethousand_534: u16 = 0b1111_1111_1111_1110;
    let sixtyfivethousand_535: u16 = 0b1111_1111_1111_1111;

    print!("{}, {}, {}, ..., ", zero, one, two);
    println!("{}, {}, {}", sixtyfivethousand_533, sixtyfivethousand_534, sixtyfivethousand_535);
}

当编译后，listing打印了下面这短短的一行：

0, 1, 2, ..., 65533, 65534, 65535

尝试通过rustc -O ch5-to-oblivioin.rs在开启优化的情况下编译代码，并运行编译后的可执行文件。行为有点不同，我们感兴趣的问题是当没有剩余的位时会发生什么，65536无法通过u16表示。（应该是在说我们无法通过字面量形式将65535赋值给u16变量，这样无法通过编译）

有一个更简单的使用类似技术杀掉一个程序的方法。在listing 5.5中，我们让Rust向u8中填入400，而它实际只能容纳255个值。看下面的listing中的内容：

// 下面这行是必须的，rust编译器可以检测到这种明显的溢出情况（所以必须加上它让编译器忽略）
#[allow(arithmetic_overflow)]
fn main() {
    let (a, b) = (200, 200);
    let c: u8 = a + b;
    println!("200 + 200 = {}", c);
}

代码编译了，但是下面两件事发生了：

• 程序panic：

  thread 'main' panicked at 'attempt to add with overflow', examples/ch5-bit-patterns.rs:4:17
  stack backtrace:
      ... omit some lines ...
  note: Some details are omitted, run with `RUST_BACKTRACE=full` for a verbose backtrace.
  

  这个行为可以在使用rustc的默认选项下发生

  rustc ch5-impossible-add.rs && ch5-impossible-add
  

• 程序给了你错误的答案：

  200 + 200 = 144
  

  这个行为会在使用-O参数执行rustc时发生

  rustc -O ch5-impossible-add.rs && ch5-impossible-add
  

这里有两个小知识：

• 理解你所使用的类型的限制是很重要的
• 即使Rust很强，用Rust编写的程序依然可能会歇菜

开发防止整数溢出的策略是系统程序员区别于其它程序员的方式之一。只有动态类型语言经验的程序员几乎不太可能遇到整数溢出。动态语言通常检测整数表达式的结果可以匹配类型的限制，当它们不能时，接收结果的变量就会变成一个更宽的整数类型。

当开发一个性能很重要的代码时，你可以选择要调整的参数。如果你使用一个固定大小的类型，你获得了速度，但是你需要接受一些风险。为了减轻这些风险，你可以检查溢出不会在运行时发生，同时，施加这些检查会拖慢你的效率。另外，更广泛的一个选项是，牺牲空间，使用更大的整数类型，比如i64。当你仍需要更大时，你可以选择任意大的整数，当然，它们也有自己的成本。

理解字节顺序

CPU厂商们争论的是构成整数的独立字节该如何排列。一些CPU将多个字节的序列从左到右排列，而另一些则从右到左排列，这被称为CPU的字节顺序（endianness）。这也是为什么复制一台计算机上的可执行程序到另一台计算机上可能不可用的原因之一。

译者：字节顺序是指多个字节之间的排序方式，别用位来思考，昨天没细看我就陷进去了，数了半天数

让我们考虑一个32位的整数，它其中有四个字节：AA、BB、CC以及DD。Listing 5.6中，在我们的老朋友sys::mem::transmute()的帮助下，展示了字节序带来的问题。当编译并执行后，listing5.6中的代码可能是两种输出其中之一，这取决于你机器的字节顺序。大多数人们日常工作的计算机会打印如下内容：

-573785174 vs. -1430532899

但是更加少见的硬件会交换两个数，就像这样：

-1430532899 vs. -573785174

// Listing 5.6
use std::mem::transmute;

fn main() {
    let big_endian: [u8; 4] = [0xAA, 0xBB, 0xCC, 0xDD];
    let little_endian: [u8; 4] = [0xDD, 0xCC, 0xBB, 0xAA];

    let a: i32 = unsafe { transmute(big_endian) };
    let b: i32 = unsafe { transmute(little_endian) };

    println!("{} vs. {}", a, b);

}

术语来自于字节序列中字节的意义，我们回到学习加法的时候，我们可以将数字123分解成三个部分：

表达式	结果
100x1	100
10x2	20
1x3	3

将所有这些部分相加，我们得到了初始的数字。第一部分，100，是重要的部分（系数最大）。当我们使用惯常的方式来写这个数字时，我们把123写作123，这就是大端法格式。当我们反转这个顺序，将123写成321，这就是小端法格式。

二进制数也是一样的。每一个数字部分是2的一个幂次（\(2^0, 2^1, 2^2, ..., 2^n\)）。

在1990年代后期，字节顺序是一个大问题，尤其是在服务器市场上。由于忽略了很多处理器可以支持双端字节序这一事实，Sun Microsystems、Cray、Motorola以及SGI都选择了其中一条路（大端或小端）。ARM开发了一款双端架构，Intel则走向了另一条路，显然另一条路赢了。整数几乎全部以小端法存储。

除了多字节序列的问题，这还有一个相关的字节问题。一个代表3的u8类型数据，它应该看起来像0000_0011还是1100_0000？计算机的独立位布局偏好被称为位顺序（bit endiannes或bit numbering）。不过无论如何，这种内部顺序很难影响到你每天的编程。如果想进一步了解的话，去看看你的平台的文档，看看最重要的位被排在了哪一边？

表示小数数字

我在这一章开始的时候说过，更多的了解位模式可以让你压缩你的数据。让我们到实践中来。在这一部分，你将学到如何提取位来表示一个浮点数，并且将这些注入到一个你自己创造的单字节格式中。

现在，我们手里有一些困难。机器学习的那些实践者们通常需要存储以及分派很大的模型，我们这里的目标中的一个模型仅仅是一个数字（小数）数组。这些模型中的数字经常落在0..=1或-1..=1的范围中，这取决于具体的应用。从给定的信息来看，我们不需要f32或f64的完整范围，为什么要使用所有的字节呢？让我们看看只使用1个字节能走多远。因为我们有一个已知的有限范围，所以创建一个可以紧凑的模拟这个范围的的十进制数字格式是可能的。

开始前，我们需要学学，在当今的计算机中，小数数据是如何表示的。

浮点数

每一个浮点数在内存中都使用科学计数法表示，如果你不熟悉科学计数法，这是一个简单的入门

科学家们使用\(1.898 \times 10^{27}\)来描述木星的质量，使用\(3.801 \times 10^{-4}\)来描述蚂蚁的质量。这一计数法的本质是可以使用相同数量的字符来描述具有截然不同的规模的数字。计算机科学家们将这一优点提取，来创建一个固定宽度的格式来编码大量的数字。一个数字中的每一位在科学计数法中都有一个角色：

• 符号：我们的两个例子中没有显式出现，它用于表示负数（负无穷到零）
• 尾数/数值部分（mantissa/significand）：例子中的1.898、3.801
• 基数（radix/base）：我们例子中的10
• 指数（exponent）：数值的规模，也就是我们例子中的27和-4

可以很轻易地从浮点数中找到这些概念，一个浮点数是一个具有三个属性的容器：

• 一个符号位
• 一个指数
• 一个数值部分

看看f32内部

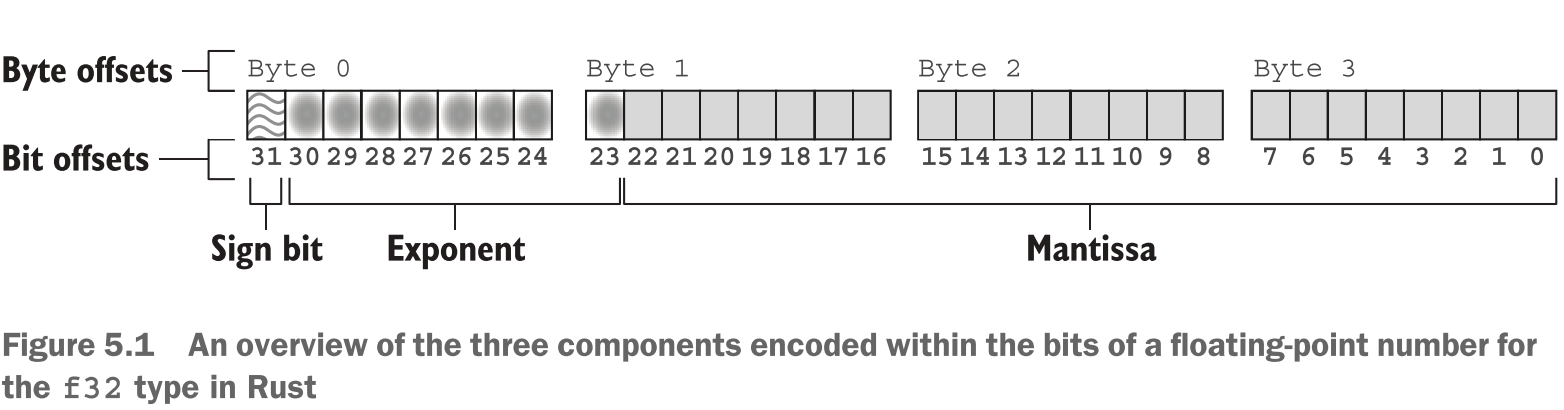
图5.1展示了Rust中f32类型的内存布局。这个布局在IEEE 754-2019与IEEE 754-2008标准中被称作binary32，它们的前身在IEE 754-1985中被称作single。

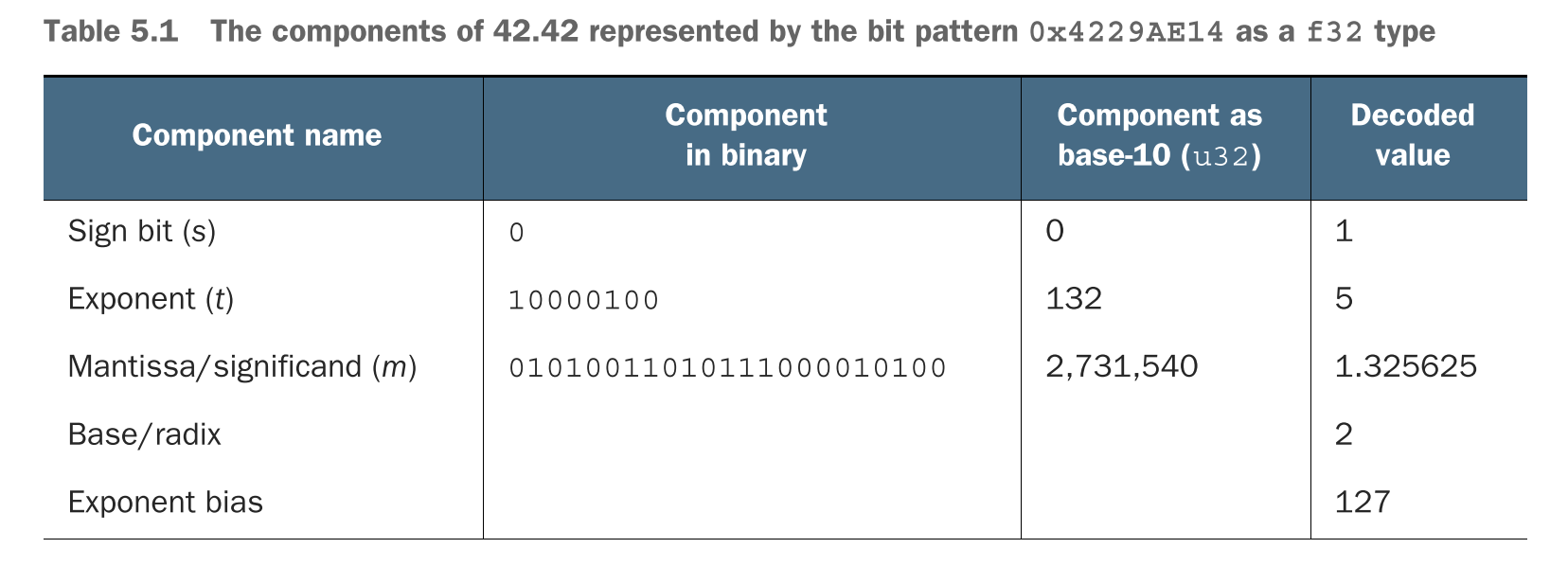
值42.42被编码成具有位模式01000010001010011010111000010100的f32数据。这个位模式可以更紧凑的写成0x4229AE14。表5.1展示了（浮点数的）三个属性的值以及它们代表了什么

下面的等式将浮点数的属性解码成单一数字（用人话来说就是具有三个属性的浮点数位模式如何代表一个具体的小数）。标准中的变量（Radix、Bias）使用首字母大写的格式来写，位模式中的变量（sign_bit、mantissa、exponent）使用小写字母来写。

\[n=-1^{sign\_bit}\times mantissa\times Radix^{(exponent-Bias)}\\ n=-1^{sign\_bit}\times mantissa\times Radix^{(exponent-127)}\\ n=-1^{sign\_bit}\times mantissa\times Radix^{(132-127)}\\ n=-1^{sign\_bit}\times mantissa\times 2^{(132-127)}\\ n=-1^{sign\_bit}\times 1.325625\times 2^{(132-127)}\\ n=-1^{0}\times 1.325625\times 2^{5}\\ n=1\times 1.325625\times 32\\ n=42.42 \]

浮点数中的一个怪事是，sign_bit允许正0和负0出现，也就是说，不同的位模式比较起来可能是相同的（0和-0），并且相同的位模式比较起来可能是不同的（NAN值）。

抽取符号位

为了抽取符号位，需要将其它的位移开。比如f32，右移31位（>>31）。下面的listing是一个简短的执行右移的代码片段：

// Listing 5.7
fn main() {
    let n: f32 = 42.42;
    let n_bits: u32 = n.to_bits();
    let sign_bit = n_bits >> 31;
    // 译者自己添加的代码
    // if sign_bit == 0 {
    //     println!("positive");
    // } else {
    //     println!("negative");
    // }
}

为了保证你对发生了什么有一个更深的直觉，下面用图形绘制了详情：

1. 从一个f32值开始

   let n: f32 = 42.42;
   

2. 使用u32来解释f32的位，以允许位运算：

   let n_bits: u32 = n.to_bits();
   

   
3. 将位右移31个位置：

   let sign_bit = n_bits >> 31;
   

   

抽取指数

为了抽取指数，必须有两个位运算。第一个，执行一个右移来覆盖数值位（>>23），然后使用AND掩码（& 0xff）来排除符号位（因为指数位有8位，右移23后剩9位，掩码排除了最高位）。

指数位仍需要进行解码，为了解码指数位，将它解释为一个8位的有符号整数，然后从结果中减去127。（就像我们在5.3.2节中讨论的，127是bias）下面的listing展示了描述上两段的步骤的代码。

let n: f32 = 42.42;
let n_bits: u32 = n.to_bits();
let exponent_ = n_bits >> 23;
let exponent_ = exponent_ & 0xff;
let exponent = (exponent_ as i32) - 127;

解释：

1. 从f32数字开始

   let n: f32 = 42.42;
   

2. 解释f32到u32以允许位运算

   let n_bits: u32 = n.to_bits();
   

   

3. 移动指数的8位到右侧，以覆盖数值位：

   let exponent_ = n_bits >> 23;
   

   

4. 使用AND掩码过滤符号位，只有右侧八位可以通过掩码：

   let exponent_ = exponent_ & 0xff;
   

   

5. 将剩下的位解释成一个有符号整数然后减去标准中定义的bias

   let exponent = (exponent_ as i32) - 127;
   

抽取数值位

为了抽取数值位的23位，你可以使用一个AND掩码区溢出符号位以及指数位（& 0x7fffff）。然而你实际上不需要这样做，因为随后的解码步骤可以简单的忽略这些无关的位。不幸的是，数值位的解码步骤要比指数复杂很多。

为了解码数值位，使用每一位的权重乘以每一位，然后将结果相加。第一位的权重是0.5（\(2^{-1}\)），后续的每一个位的权重都是当前权重的一半，例如：0.5（\(2^{-1}\)）、0.25（\(2^{-2}\)）、...、0.00000011920928955078125 (\(2^{–23}\))。一个隐式的第24位可以表示为1.0（\(2^{-0}\)）总被认为是存在的，除非触发特殊情况。特殊情况可以被如下的指数状态触发：

• 当指数位全为0，数值位将作为次正规数表示（也叫非正规数）。实际而言，这个改变让小数可以表示更加接近0的数，一个次正规数是一个在0与正规数行为下能表示的最小数之间的数。
• 当指数位全为1，小数表示无穷大和负无穷，或者Not a Number（NAN）。NAN值代表数值结果在数学上未定义的特殊情况（比如0 / 0）或者其它无效值。

引入NAN值的操作通常是违反直觉的。例如，测试两个值是否相等总会返回false，尽管两个位模式实际是一样的。一个有趣的事儿是f32有大约4.2亿个（\(~2^{22}\)）个位模式可以表示NAN。

下面的listing提供了非特殊情况下代码的实现：

// Listing 5.9
let n: f32 = 42.42;
let n_bits: u32 = n.to_bits();
let mut mantissa: f32 = 1.0;
for i in 0..23 {
    let mask = 1 << i;
    let one_at_bit_i = n_bits & mask;
    if one_at_bit_i != 0 {
        let i_ = i as f32;
        let weight = 2_f32.powf( i_ - 23.0 );
        mantissa += weight;
    }
}

再次慢放上面的过程：

1. 从f32值开始：

   let n: f32 = 42.42;
   

2. 将f32转为u32以允许位运算：

   let n_bits: u32 = n.to_bits();
   

3. 创建一个可变的f32值初始化为1.0（\(2^{-0}\)）。这代表隐含的24位的权重：

   let mut mantissa: f32 = 1.0;
   

4. 迭代计算数值位的小数位，添加这些这些位所代表的值到mantissa变量中：

   for i in 0..23 {
       let mask = 1 << i;
       let one_at_bit_i = n_bits & mask;
       if one_at_bit_i != 0 {
           let i_ = i as f32;
           let weight = 2_f32.powf( i_ - 23.0 );
           mantissa += weight;
       }
   }
   

   1. 使用一个临时变量i作为迭代数，从0迭代到23

      for i in 0..23 {
      

   2. 创建一个位掩码，将迭代号i作为允许通过的位，并将结果分配给mask

      let mask = 1 << i;
      

   3. 使用mask作为一个保存在n_bits中的原始数的过滤器，当原始数的第\(i\)位不是0时，one_at_bit_i将被赋予一个非零值

      let one_at_bit_i = n_bits & mask;
      

   4. 如果one_at_bit_i是非零，则执行：

      if one_at_bit_i != 0 {
      

   5. 计算在位置\(i\)处的位的权重，公式是：\(2^{i-23}\)

      let i_ = i as f32;
      let weight = 2_f32.powf( i_ - 23.0 );
      

   6. 原地添加权重到mantissa

      mantissa += weight;
      

解析Rust的浮点字面量比看起来要难
Rust的数字具有方法。为了返回离1.2更近的整数，rust使用1.2_f32.ceil()方法而不是ceil(1.2)这一函数调用。虽然这通常很方便，但这会在编译器解析你代码时导致一些问题。

举例来说，一元负号的优先级低于方法调用，这意味着可能发生预期之外的数学异常。使用括号来向编译器澄清你的意图是有帮助的。为了计算\(-1^0\)，将\(1.0\)包裹在括号中：

(-1.0_f32).powf(0.0)

而不是

-1.0_f32.powf(0.0)

这将会被解释成\(-(1^0)\)，因为\(-1^0\)和\(-(1^0)\)在数学上都是有效的，Rust将不会在你省略括号时抗议。

解剖一个浮点数

就像在5.4节开始时提到的，浮点数是一个具有三个属性的容器的格式，5.4.1到5.4.3节已经给了我们解剖每一个属性的工具，让我们把它们放到工作中。

Listing 5.10干了一个往返，它解剖了数字42.42的每一个属性，编码为f32的多个独立部分，然后再将它们整合起来创建另一个数字。为了将一个浮点数中的位转换成另一个浮点数，有三个任务要做：

1. 从容器中解开这些值的位（1到26行上的to_parts()）
2. 从它们的原始位模式中解码每个值到实际的值（28到47行的decode()）
3. 执行转换科学计数法到一个普通数字的转换（49到55行的from_parts()）

当我们运行listing 5.10时，它提供了编码成一个f32的数——42.42内部的两个视图：、

42.42 -> 42.42
field     |  as bits | as real number
sign      |        0 | 1
exponent  | 10000100 | 32
mantissa  | 01010011010111000010100 | 1.325625

在listing 5.10中，deconstruct_f32()使用位运算技术解剖了浮点数值的每一个属性。decode_f32_parts()展示了如何转换这些属性到相关的数。f32_from_parts()方法组合这些去创建一个单一的小数。

// Listing 5.10 复制它的代码比较难，译者这个代码和原书的稍有出入
fn to_parts(float: f32) -> (u32, u32, u32) {
    let n_bits: u32 = float.to_bits();
    let sign_bit = n_bits >> 31;
    let exponent_bit = (n_bits >> 23) & 0xff;
    let mantissa_bit = n_bits & 0x7fffff;
    (sign_bit, exponent_bit, mantissa_bit)
}

fn decode_f32_parts(
    sign_bit: u32,
    exponent_bit: u32,
    mantissa_bit: u32
) -> (f32, f32, f32) {
    let sign = (-1.0f32).powf(sign_bit as f32);
    let exponent = (exponent_bit as i32) - 127;
    let exponent = 2f32.powf(exponent as f32);

    let mut mantissa = 1.0;

    for i in 0..23 {
        let mask = 1 << i;
        if mantissa_bit & mask != 0 {
            let weight = 2f32.powf((i as f32) - 23.0);
            mantissa += weight;
        }
    }

    (sign, exponent, mantissa)
}

fn from_parts(sign: f32, exponent: f32, mantissa: f32) -> f32 {
    sign * exponent * mantissa
}

fn main() {
    let n: f32 = 42.42;

    let (sign_bit, exponent_bit, mantissa_bit)  = to_parts(n);
    let (sign, exponent, mantissa) = decode_f32_parts(sign_bit, exponent_bit, mantissa_bit);
    let result = from_parts(sign, exponent, mantissa);

    println!("{}", result);
}

理解如何从字节中解出位，意味着在你的职业生涯中，当你面对着需要解释从网络中传递过来的无类型字节的问题时，你将处于更有利的位置。

定点数格式

除了浮点数之外，定点数也可以用来表示小数。它们在表示分数以及没有浮点单元（FPU）的CPU上（比如微控制器）执行计算时非常有用。不像浮点数，它的小数位数不可以动态的移动以使用不同的范围。在我们的例子中，我们将使用一个定点数格式来紧凑的表示-1..=1之间的值，尽管它会损失精度，但它显著的节省了空间。

Q格式是一个使用单一字节的定点数格式，它是德州仪器公司为了嵌入式计算设备创建的，我们将实现的Q格式的确切版本被称作Q7。这代表其中有7个位可以用于表示数字，以及一个符号位。我们将通过将7个位隐藏在一个i8中来伪装小数。这意味着Rust编译器可以帮助我们持续跟踪值的符号（因为i8也是通过高位的符号位来表示正负）。我们将derive（衍生）一些traits，比如PartialEq和Eq，它们为我们的类型提供了无成本的比较操作。

下面的listing，一个从listing 5.14中提取的代码，提供了类型定义：

#[derive(Debug,Clone,Copy,PartialEq,Eq)]
pub struct Q7(i8);

一个从未命名属性中创建的结构体（例如Q7(i8)）被称为元组结构体，在你没有希望直接访问属性的意图时，这种结构体提供了一个简洁的写法。listing 5.11中没有展示出的一点是，元组结构体可以包含多个属性，你可以将它们用逗号隔开。作为提醒，#[derive(...)]块告诉Rust，帮助我们自动实现一些trait：

• Debug——被println!()宏（以及其它）使用，允许Q7被通过{:?}语法转换成一个字符串
• Clone——让Q7可以通过.clone()方法被克隆，因为i8实现了Clonetrait，所以我们可以直接使用derive衍生。
• Copy——在可能发生所有权问题或其他问题的地方，能够实现廉价和隐式的复制。说人话，就是让Q7在使用移动语义（move semantics）时转而使用复制语义（copy semantics）
• PartialEq——让Q7的值可以通过==符号来比较相等性
• Eq——向Rust知名，所有可能的Q7值都可以和任何可能的Q7值相比较

我们只是想把Q7设计成一个对于存储和数据传输都足够紧凑的类型。最重要的是到浮点数的转换和转回。下面的listing是5.14中的一部分，展示了到f64的转换：

// Listing 5.12
impl From<f64> for Q7 {
    fn from(n: f64) -> Self {
        if n >= 1.0 {
            Q7(127)
        } else if n<= -1.0 {
            Q7(-128)
        } else {
            Q7((n * 128.0) as i8)
        }
    }
}

impl From<Q7> for f64 {
    fn from(q7: Q7) -> Self {
        // 除以128
        (q7.0 as f64) * 2f64.powf(-7.0)
    }
}

listing 5.12中的两个impl From<T> for U向Rust解释了如何将T转换为U。

TIP：使用Fromtrait的转换应该是数学等价的。对于可能会失败的转换，考虑实现std::convert::TryFromtrait。

有了我们刚刚看到的From<f64>实现，我们可以很快的实现f32到Q7的转换。下面的listing，是从listing 5.14中提取的一部分。

// Listing 5.14
impl From<f32> for Q7 {
    fn from(n: f32) -> Self {
        Q7::from(n as f64)
    }
}

impl From<Q7> for f32 {
    fn from(q7: Q7) -> Self {
        f64::from(q7) as f32
    }
}

现在，我们已经覆盖了两种浮点数，但我们如何知道我们编写的代码实际做了我们想做的事呢？并且我们如何测试我们写的这玩意儿。通过cargo，Rust有了优秀的单元测试支持。

现在，你看到过的Q7代码已经可以作为一个完整的listing了，但在那之前，我们要先测试一下。进入crate的根目录，运行cargo test，下面展示的是listing 5.14的输出

   Compiling test_rust_project v0.1.0 (/mnt/d/WorkSpace/Sources/Rust/test_rust_project)
    Finished test [unoptimized + debuginfo] target(s) in 2.07s                   
     Running unittests examples/q7.rs (target/debug/examples/q7-fdd15277db77a05c)

running 3 tests
test tests::f32_to_q7 ... ok    
test tests::out_of_bounds ... ok
test tests::q7_to_f32 ... ok    

test result: ok. 3 passed; 0 failed; 0 ignored; 0 measured; 0 filtered out; finished in 0.00s

从随机字节中生成随机概率

这有一个有趣的练习来测试你对前面的知识的掌握程度。想象你有一个随机的字节来源（u8），并且你想要转换其中的一个到一个值再0到1之间的浮点数中（f32）。Naively interpreting the incoming bytes as f32/f64 via mem::transmute results in massive variations in scale. 下面的listing展示了使用除法操作来从一个任意的输入字节生成一个在0到1之间的f32值

// Listing 5.15
fn mock_rand(n: u8) -> f32 {
    // 255是u8能表示的最大值
    n as f32 / 255.0
}

除法是一个慢操作，或许有一些比简单的除以一个字节能表示的最大值更快的办法。也许我们可以利用f32的三个属性，我们可以假设一个恒定的指数值，然后将输入位（输入u8）位移到数值位上，这样，就可以构成一个0道义之间的范围。Listing5.16使用了位运算，这是我能达到的最棒的代码了

使用-1作为指数，可以表示为0b01111110（十进制中的126），原字节可以被映射到0.5到0.998之间，我们可以把它标准化到0.0到0.996，只需要做减法和乘法操作，但是真的没有更好的办法了吗？

// Listing 5.16
fn mock_rand(n: u8) -> f32 {
    let base = 0b0_01111110_00000000000000000000000;

    let large_n = (n as u32) << 15;

    let f32_bits = base | large_n;

    let m = f32::from_bits(f32_bits);

    2.0 * (m - 0.5)
}

作为一个完整的程序，你可以很轻松将listing5.16放到一个测试程序中。Listing 5.17从任意输入字节生成一个在0到1之间的小数，并且完全没用到除法。下面是输出：

max of input range: 11111111 -> 0.99609375
mid of input range: 01111111 -> 0.49609375
min of input range: 00000000 -> 0.0

// Listing 5.17
fn mock_rand(n: u8) -> f32 {
    let base = 0b0_01111110_00000000000000000000000;
    let large_n = (n as u32) << 15;
    let f32_bits = base | large_n;
    let m = f32::from_bits(f32_bits);
    2.0 * (m - 0.5)
}

fn main() {
    println!("max of input range: {:08b} -> {:?}", 0xff, mock_rand(0xff));
    println!("mid of input range: {:08b} -> {:?}", 0x7f, mock_rand(0x7f));
    println!("min of input range: {:08b} -> {:?}", 0x00, mock_rand(0x00));
}

实现一个CPU模拟器以建立函数也是数据的观念

一个相当平凡且耐人寻味的有关计算的细节是——指令也只是一堆数字。操作和数据共享同一种编码，这意味着，作为一个通用的计算设备，你的计算机可以通过软件来模拟其它的计算机指令集。虽然我们不能剥开一个CPU来看看其内部是如何工作的，但我们可以使用代码构建一个。

在这一部分后，你将学到一个计算机的底层是如何操作的。这一部分向你展示了函数是如何操作的以及术语——指针的含义。我们不会使用汇编语言，我们实际上直接通过十六进制编程。这一部分也向你介绍了另一个你曾经可能听过的术语——栈。

我们将实现一个叫做CHIP-8系统的子集，它于1970年代上市。CHIP-8被一众厂商支持，但是即使是按照当时的标准，它也可以说是相当原始。（相比起商业用途或科学应用，它被创建的目的更多是用来编写游戏）

一个曾经使用CHIP-8 CPU的设备是COSMAC VIP。它有一个64x32分辨率的单色显示屏，2KB的内存，1.76MHz的CPU，以及275美元的售价，你还需要自己组装电脑，其内部包含一个由世界上第一个女性游戏开发者——Joyce Weisbecker编程的游戏。

CPU RIA/1：地址

我们将从构建一个迷你的核心来开始构建我们对其的理解。我们首先构建一个只支持单一指令的模拟器，即加法指令。为了理解本节中的listing 5.22发生了什么，我们有三个主要的东西要学习：

• 熟悉新术语
• 如何解释操作码（opcodes）
• 理解主循环

与CPU模拟相关的术语

• 一个操作（operation，经常缩写成“op”）代表系统本身支持的程序。在你继续探索的过程中，你也可能遇到含义类似的短语，比如在硬件中实现的或内部操作。
• 寄存器是CPU可以直接访问的数据的容器。对于大部分操作，操作数必须移动到寄存器中，操作才能发生作用，对于CHIP-8，每一个寄存器是一个u8值
• 一个操作码是一个映射到指定操作上的数字。在CHIP-8平台上，操作码包含操作以及操作符寄存器。

定义CPU

我们想要支持的第一个操作是加法，该操作需要两个寄存器（x和y）作为操作数，并且将存储在y中的值加到x上。我们尽可能使用最少的代码来实现它，就像下面的listing那样。我们的CPU初始只包含两个寄存器以及一个单个操作码的空间。

// Listing 5.18
struct CPU {
    current_operation: u16, // 所有在CHIP-8操作码都是u16值
    registers: [u8; 2],     // 这两个寄存器足够用于加法
}

目前为止，CPU还无法工作起来，为了执行加法，我们需要做如下几步，但是我们现在还没有将数据存储在内存中的能力。

1. 初始化一个CPU
2. 加载u8值到registers
3. 加载加法操作码到current_operation
4. 执行操作

加载值到寄存器

启动CPU的过程包括写入在CPU结构中定义的属性。下面的listing，是从listing 5.22中提取出的，展示了CPU初始化进程。

// Listing 5.19
fn main() {
    let mut cpu = CPU {
        current_operation: 0,
        registers: [0; 2]
    };

    cpu.current_operation = 0x8014;
    cpu.registers[0] = 5;
    cpu.registers[1] = 10;
}

listing 5.19的第38行在没有上下文的情况下，很难解释。常数0x8014是CPU将要解释的操作码，为了解码它，将它分割成四个部分：

• 8意味着该操作卷入两个寄存器
• 0意味着cpu.register[0]
• 1意味着cpu.register[1]
• 4意味着加法操作

理解模拟器的主循环

现在，我们已经加载了数据，CPU已经可以做一些工作了。run()方法执行一批我们的模拟操作，使用接下来的步骤，它模拟CPU循环：

1. 读取操作码（通常从内存）
2. 解码指令
3. 匹配解码的指令来获知操作码
4. 将操作的执行，派发到一个指定函数上

下面的listing是从5.22中提取出的代码，它展示了第一个功能已经被添加到我们的模拟器中：

// Listing 5.20
impl CPU {
    fn read_opcode(&self) -> u16 {
        self.current_operation
    }
    fn run(&mut self) {
        let opcode = self.read_opcode();

        let c = ((opcode & 0xF000) >> 12) as u8;
        let x = ((opcode & 0x0F00) >> 8) as u8;
        let y = ((opcode & 0x00F0) >> 4) as u8;
        let d = ((opcode & 0x000F) >> 0) as u8;

        match (c, x, y, d) {
            (0x8, _, _, d) => self.add_xy(x, y),
            _ => todo!("opcode {:04x}", opcode),
        }
    }
    
    fn add_xy(&mut self, x: u8, y: u8) {
        self.registers[x as usize] += self.registers[y as usize];
    }
}

如何解释CHIP-8操作码

很重要的一件事儿是我们的CPU要能解释它的操作码（0x8014），这一部分对CHIP-8采用的程序以及它的命名规范进行详尽的解释。

CHIP-8的操作码是由4个半字节（nibbles）组成的u16值，也就是说，一个nibble是一个4位值，因为Rust中没有4位的类型，所以，拆解u16值到它们各自的部分上是一个棘手的事。更复杂的是，CHIP-8的字段经常被重新组合，以形成8位或12位的值，这取决于上下文。

为了简便的讨论操作码中每一部分，我们引入一些标准术语。每一个操作码由两个字节组成，高字节（high byte）以及低字节（low byte）。并且，相应地，每一个字节都由两个半字节组成，高半字节（high nibble）以及低半字节（low nibble），图5.2描述了每一个术语：

CHIP-8的操作手册引入了多种变量，包括\(kk\)，\(nnn\)，\(x\)以及\(y\)。表格5.2解释了它们的用途，位置以及宽度。

* n和d占据了相同的位置，但是它们只会在不同的，互斥的上下文中出现
† 变量c和d只在这本书里使用，没有出现在其它CHIP-8文档中
‡ 在CPU RIA/3（listing 5.29）中使用

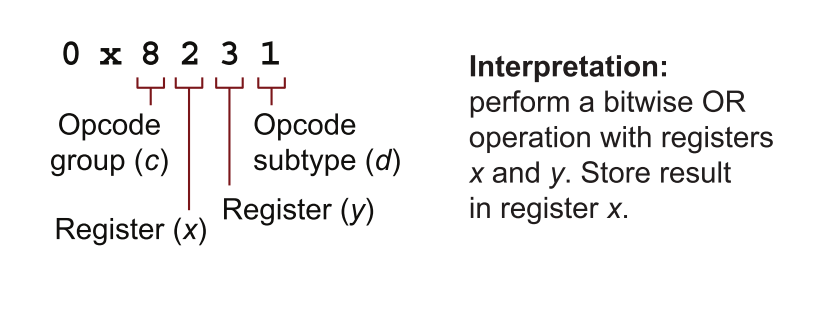
操作码有三种主要形式，就像图片5.3中描述的，解码过程需要匹配第一个字节的高nibble，然后来应用三种策略中的一种：

为了从字节序列中解出nibble，我们需要使用右移（>>）以及逻辑与（&）位操作。这些操作已经在5.4中引入过了，尤其是在5.4.1到5.4.3。下面的listing展示了应用这些位操作到目前的问题上：

// Listing 5.21
fn main() {
    let opcode: u16 = 0x71E4;
    
    let c = ((opcode & 0xF000) >> 12) as u8;
    let x = ((opcode & 0x0F00) >> 8) as u8;
    let y = ((opcode & 0x00F0) >> 4) as u8;
    let d = ((opcode & 0x000F) >> 0) as u8;
    
    assert_eq!(c, 0x7);
    assert_eq!(x, 0x1);
    assert_eq!(y, 0xE);
    assert_eq!(d, 0x4);
    
    let nnn = opcode & 0x0FFF;
    let kk = opcode & 0x00FF;
    
    assert_eq!(nnn, 0x1E4);
    assert_eq!(kk,   0xE4);
}

现在，我们已经能够解码指令了，下一步就是实际的去执行他们。

CPU RIA/1：加法器 完整代码

// Listing 5.22
struct CPU {
    current_operation: u16,
    registers: [u8; 2],
}

impl CPU {
    fn read_opcode(&self) -> u16 {
        self.current_operation
    }
    fn run(&mut self) {
        let opcode = self.read_opcode();

        let c = ((opcode & 0xF000) >> 12) as u8;
        let x = ((opcode & 0x0F00) >> 8) as u8;
        let y = ((opcode & 0x00F0) >> 4) as u8;
        let d = ((opcode & 0x000F) >> 0) as u8;

        match (c, x, y, d) {
            (0x8, _, _, d) => self.add_xy(x, y),
            _ => todo!("opcode {:04x}", opcode),
        }
    }

    fn add_xy(&mut self, x: u8, y: u8) {
        self.registers[x as usize] += self.registers[y as usize];
    }
}

fn main() {
    let mut cpu = CPU {
        current_operation: 0,
        registers: [0; 2]
    };

    cpu.current_operation = 0x8014;
    cpu.registers[0] = 5;
    cpu.registers[1] = 10;


    cpu.run();

    assert_eq!(cpu.registers[0], 15);

    println!("5 + 10 = {}", cpu.registers[0]);
}

CPU RIA/2：Multiplier

CPU RIA/1 可以执行一个单一指令：加法。 CPU RIA/2具有了Multiplier，可以执行序列中的多个指令。这个Multiplier包括RAM，一个工作的主循环，一个用于指示下面要执行那一条指令的变量，我们称作position_in_memory。Listing 5.26对5.22做了如下实质性的修改：

译者：这个Multiplier，译者本来以为是乘法器，但实际书上的意思应该是多路复用的意思？让CPU可以连续执行多条指令？也可能是什么专有名词，我也不知道。

• 添加4KB的内存（第8行）
• 包含一个完整的主循环以及停止条件（14到31行）
  在循环的每一步骤里，position_in_memory处的内存都将被访问并且解码成一个操作码。position_in_memory随后递增到下一个内存地址上，并且操作码被执行。CPU继续持续运行直到停止条件（遇到一个0x0000操作码）
• 移除CPU结构中的current_instruction属性，它被替换成了主循环中的一部分，从内存中解码字节（15到17行）
• 将操作码写入内存（51到53行）

扩展CPU以支持内存

我们需要进行一些修改来让我们的CPU更加有用，第一步，计算机需要内存。

Listing 5.23，也是从5.26中提取的代码，提供了CPU RIA2的定义。CPU RIA/2包含通用的寄存器用于运算，以及一个特殊用途的寄存器（position_in_memory）。方便起见，我们在CPU结构本身中使用memory属性包含系统内存。

// Listing 5.23
struct CPU {
    memory: [u8; 0x1000],
    // 使用usize替代u16是因为Rust允许使用usize来做索引
    position_in_memory: usize,
    registers: [u8; 2],
}

现在CPU有了些新玩意儿：

• 有了16个寄存器，这意味着可以使用一个单一的十六进制数（0到F）来寻址它们。这允许所有的操作码都可以紧凑的表示成u16值
• CHIP8只有4096字节的内存（也就是16进制的0x1000），这使得CHIP-8的usize类型只有12位宽，因为\(2^12=4096\)。这12位来自于我们前面讨论过的变量nnn

本书在两个方面没有遵守标准：

• 我们所说的“position in memory”通常被称作“program counter”（程序计数器 PC）。作为一个新手，程序计数器这个名字可能会让你难以理解，所以，本书使用了一个能够反映它用途的名字。
• 在CHIP-8定义中，前512字节（0x100）被系统保留，其它字节由程序所有。我们的实现中没有这一限制。

从内存中读取操作码

因为我们给CPU添加了内存，所以read_opcode()方法需要更新。下面的listing，是5.26中的一部分代码，它通过结合两个u8值到一个单一的u16值从内存中读取一个操作码。

// Listing 5.24
fn read_opcode(&self) -> u16 {
    let p = self.position_in_memory;
    let op_byte1 = self.memory[p] as u16;
    let op_byte2 = self.memory[p + 1] as u16;

    // 我们将内存中的两个值通过逻辑与操作结合，以创建一个u16的操作码，我们需要从一开始就将它们转换为u16，否则，左移操作将会把所有位置为0
    op_byte1 << 8 | op_byte2
}

处理整数溢出

在CHIP-8中，我们将最后一个寄存器作为一个carry flag，当它被设置，就代表一个操作已经溢出了u8寄存器的大小。下面的listing是5.26中的一部分，展示了如何处理这种溢出。

// 5.26
fn add_xy(&mut self, x: u8, y: u8) {
    let from = self.registers[x as usize];
    let to = self.registers[y as usize];

    // overflowing_add方法返回(u8, bool)，bool代表是否检测到溢出发生
    let (val, overflow) = from.overflowing_add(to);

    self.registers[x as usize] = val;

    // 检测到溢出，第十六个寄存器（carry flag）置1
    if overflow {
        self.registers[0xF] = 1;
    } else {
        self.registers[0xF] = 0;
    }
}

CPU RIA/2：Multiplier 完整代码

下面的listing展示了我们的第二版模拟器的全部代码

// Listing 5.26
struct CPU {
    memory: [u8; 0x1000],
    position_in_memory: usize,
    registers: [u8; 16],
}

impl CPU {
    fn read_opcode(&self) -> u16 {
        let p = self.position_in_memory;
        let op_byte1 = self.memory[p] as u16;
        let op_byte2 = self.memory[p + 1] as u16;

        // 我们将内存中的两个值通过逻辑与操作结合，以创建一个u16的操作码，我们需要从一开始就将它们转换为u16，否则，左移操作将会把所有位置为0
        op_byte1 << 8 | op_byte2
    }

    fn run(&mut self) {
        loop {
            let opcode = self.read_opcode();
            self.position_in_memory += 2;
            let c = ((opcode & 0xF000) >> 12) as u8;
            let x = ((opcode & 0x0F00) >> 8) as u8;
            let y = ((opcode & 0x00F0) >> 4) as u8;
            let d = ((opcode & 0x000F) >> 0) as u8;

            match (c, x, y, d) {
                (0x8, _, _, d) => self.add_xy(x, y),
                (0x0, 0, 0, 0) => return,
                _ => todo!("opcode {:04x}", opcode),
            }
        }
    }

    fn add_xy(&mut self, x: u8, y: u8) {
        let from = self.registers[x as usize];
        let to = self.registers[y as usize];

        // overflowing_add方法返回(u8, bool)，bool代表是否检测到溢出发生
        let (val, overflow) = from.overflowing_add(to);

        self.registers[x as usize] = val;

        // 检测到溢出，第十六个寄存器（carry flag）置1
        if overflow {
            self.registers[0xF] = 1;
        } else {
            self.registers[0xF] = 0;
        }
    }
}

fn main() {
    let mut cpu = CPU {
        registers: [0; 16],
        memory: [0; 4096],
        position_in_memory: 0
    };

    // 初始化寄存器值
    cpu.registers[0] = 5;
    cpu.registers[1] = 10;
    cpu.registers[2] = 10;
    cpu.registers[3] = 10;

    let mem = &mut cpu.memory;

    mem[0] = 0x80; mem[1] = 0x14;  // 加载操作码 0x8014，将寄存器1加到寄存器0
    mem[2] = 0x80; mem[3] = 0x24;  // 加载操作码 0x8024，将寄存器2加到寄存器0
    mem[4] = 0x80; mem[5] = 0x34;  // 加载操作码 0x8034，将寄存器3加到寄存器0

    cpu.run();

    assert_eq!(cpu.registers[0], 35);

    println!("5 + 10 + 10 + 10 = {}", cpu.registers[0]);
}

执行，CPU RIA/2打印：

5 + 10 + 10 + 10 = 35

CPU RIA/3：调用器

我们很快就要建立完所有的模拟器功能了，这一部分，我们给模拟器添加调用函数的能力。我们没有编程语言支持，所以任何程序仍然需要使用二进制来编写。除了实现函数之外，这一部分还验证了开始时的一个断言——函数也是数据。

扩展CPU以提供一个栈

为了调用函数，我们需要实现一些额外的操作码，如下：

• CALL操作码：（0x2nnn，nnn是内存地址），设置position_in_memory到nnn，也就是函数的地址。
• RETURN操作码：（0x00EE）设置position_in_memory到上一个调用CALL操作码的内存地址

为了让这两个操作码能工作，CPU必须用一些特殊的内存来存储地址，它们被称为栈。每一个CALL操作码都会通过累加栈指针并将nnn写入栈中栈指针的位置上来向栈中添加一个地址，每一个RETURN操作码都会通过递减栈指针来移除栈顶的地址。下面的listing，是listing 5.29中的一部分，提供了我们要模拟的CPU。

struct CPU {
    memory: [u8; 0x1000],
    position_in_memory: usize,
    registers: [u8; 16],
    // 栈最大深度是16，在16个嵌套方法调用之后，程序将遇到栈溢出
    stack: [u16; 16],
    // usize类型便于在stack中进行索引
    stack_pointer: usize,
}

定义一个函数并加载到内存中

在计算机科学领域，一个函数就是一系列可被CPU执行的字节，CPU从第一个操作码开始执行，直到结尾。下面的几个代码片段演示了CPU RIA/3 如何将一系列字节转换成可执行的代码这件事变为可能。

1. 定义函数。我们的函数执行两个加法操作，然后返回，就这三行代码，麻雀虽小，五脏俱全。用类似汇编语言的标记来表示的话，这个函数的内部结构看起来应该是这样的：

   add_twice:
       0x8014
       0x8014
       0x00EE
   

2. 转换这些操作码到Rust的数据类型，翻译这三个操作码到Rust的数组语法中，使用中括号与逗号来分割每个数字。现在，函数变成了一个[u16; 3]：

   let add_twice: [u16; 3] = [
       0x8014,
       0x8014,
       0x00EE,
   ];
   

   在下一步中，我们希望使用一个字节来处理，所以我们进一步解构[u16; 3]数组到一个[u8; 6]数组中：

   let add_twice: [u8; 6] = [
       0x80, 0x14,
       0x80, 0x14,
       0x00, 0xEE,
   ];
   

3. 将这个函数加载到RAM中，假设我们希望将它加载到内存地址0x100，有两个选择，第一，如果我们的函数是一个slice类型，我们可以使用copy_from_slice()函数将它复制到memory中：

   let mem = &mut cpu.memory;
   
   let add_twice = [
       0x80, 0x14,
       0x80, 0x14,
       0x00, 0xEE,
   ];
   
   mem[0x100..0x106].copy_from_slice(&add_twice);
   

   另一个办法就是直接覆盖字节，这不需要任何临时数组：

   mem[0x100] = 0x80; mem[0x101] = 0x14;
   mem[0x102] = 0x80; mem[0x103] = 0x14;
   mem[0x104] = 0x00; mem[0x105] = 0xEE;
   

现在我们已经知道了如何加载函数到内存中了，是时候来学习如何让CPU实际的调用它了。

实现CALL和RETURN操作码

调用一个函数，拢共分三步：

1. 在栈上存储当前内存地址
2. 递增栈指针
3. 设置当前内存地址为预定的内存地址（函数的地址）

从一个函数返回，也分三步，和上面正相反：

1. 递减栈指针
2. 从栈中取出调用时的内存地址
3. 设置当前内存地址到指定的内存地址（CALL调用时的）

下面的listing，是listing5.29中的一部分，主要展示call()和ret()方法。

// Listing 5.28
fn call(&mut self, nnn: u16) {
    if self.stack_pointer > self.stack.len() {
        panic!("Stack overflow!");
    }

    self.stack[self.stack_pointer] = self.position_in_memory as u16;
    self.stack_pointer += 1;
    self.position_in_memory = nnn as usize;
}

fn ret(&mut self) {
    if self.stack_pointer == 0 {
        panic!("Stack underflow!");
    }
    
    self.stack_pointer -= 1;
    self.position_in_memory = self.stack[self.stack_pointer] as usize
}

CPU RIA/3：方法调用的完整代码

现在，万事俱备，让我们组合这些代码到一个程序中。Listing 5.29能够执行一个硬编码的数学表达式，下面是输出：

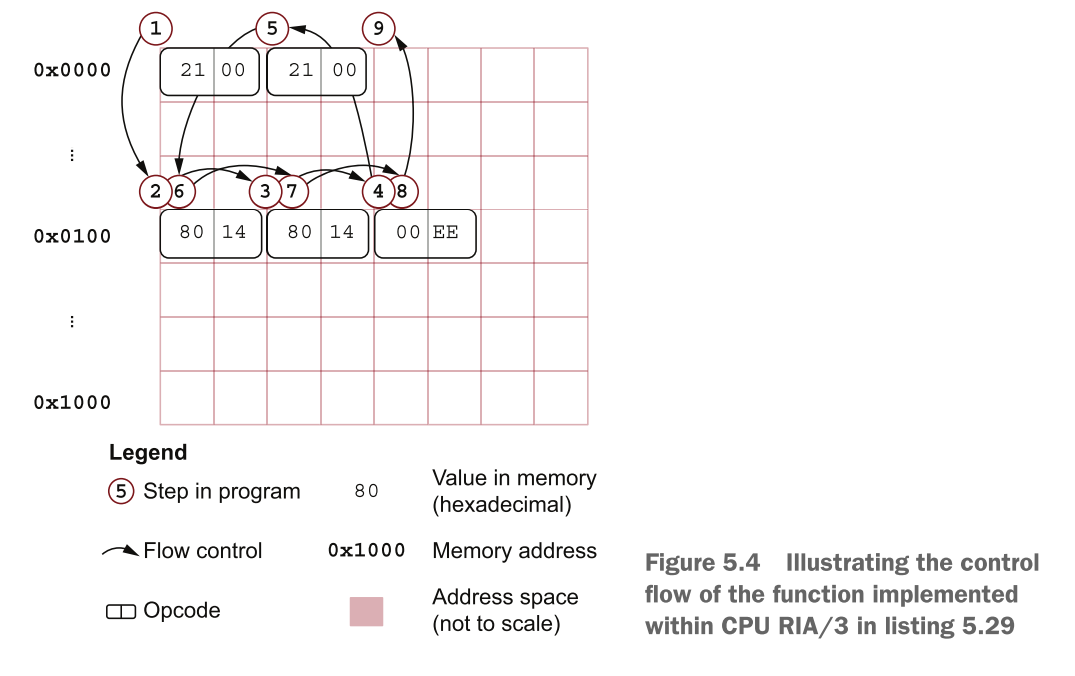
5 + (10 * 2) + (10 * 2) = 45

没有你以往熟悉的源代码了，你需要通过十六进制数来进行编程。图片5.4描述了当cpu.run()执行时发生了什么，箭头反映了程序运行过程中cpu.position_in_memory变量的状态，就像它开辟了自己的道路一样。

Listing 5.29展示了我们完整的CPU RIA/3模拟器：

// Listing 5.29
struct CPU {
    memory: [u8; 0x1000],
    position_in_memory: usize,
    registers: [u8; 16],
    stack: [u16; 16],
    stack_pointer: usize,
}

impl CPU {
    fn read_opcode(&self) -> u16 {
        let p = self.position_in_memory;
        let op_byte1 = self.memory[p] as u16;
        let op_byte2 = self.memory[p + 1] as u16;

        // 我们将内存中的两个值通过逻辑与操作结合，以创建一个u16的操作码，我们需要从一开始就将它们转换为u16，否则，左移操作将会把所有位置为0
        op_byte1 << 8 | op_byte2
    }

    fn run(&mut self) {
        loop {
            let opcode = self.read_opcode();
            self.position_in_memory += 2;
            let c = ((opcode & 0xF000) >> 12) as u8;
            let x = ((opcode & 0x0F00) >> 8) as u8;
            let y = ((opcode & 0x00F0) >> 4) as u8;
            let d = ((opcode & 0x000F) >> 0) as u8;

            let nnn = opcode & 0x0FFF;

            match (c, x, y, d) {
                (0x8, _, _, d) => self.add_xy(x, y),
                (0x2, _, _, _) => self.call(nnn),
                (0x0, 0x0, 0xE, 0xE) => self.ret(),
                (0, 0, 0, 0) => return,
                _ => todo!("opcode {:04x}", opcode),
            }
        }
    }

    fn add_xy(&mut self, x: u8, y: u8) {
        let from = self.registers[x as usize];
        let to = self.registers[y as usize];

        // overflowing_add方法返回(u8, bool)，bool代表是否检测到溢出发生
        let (val, overflow) = from.overflowing_add(to);

        self.registers[x as usize] = val;

        // 检测到溢出，第十六个寄存器（carry flag）置1
        if overflow {
            self.registers[0xF] = 1;
        } else {
            self.registers[0xF] = 0;
        }
    }

    fn call(&mut self, nnn: u16) {
        if self.stack_pointer > self.stack.len() {
            panic!("Stack overflow!");
        }

        self.stack[self.stack_pointer] = self.position_in_memory as u16;
        self.stack_pointer += 1;
        self.position_in_memory = nnn as usize;
    }

    fn ret(&mut self) {
        if self.stack_pointer == 0 {
            panic!("Stack underflow!");
        }

        self.stack_pointer -= 1;
        self.position_in_memory = self.stack[self.stack_pointer] as usize
    }
}

fn main() {
    let mut cpu = CPU {
        registers: [0; 16],
        memory: [0; 4096],
        position_in_memory: 0,
        stack_pointer: 0,
        stack: [0; 16]
    };

    // 初始化寄存器值
    cpu.registers[0] = 5;
    cpu.registers[1] = 10;
    cpu.registers[2] = 10;
    cpu.registers[3] = 10;

    let mem = &mut cpu.memory;

    // 0x2100 => CALL 100
    mem[0x000] = 0x21; mem[0x001] = 0x00;
    // 0x2100 => CALL 100
    mem[0x002] = 0x21; mem[0x003] = 0x00;
    // 0x0000 => 结束程序
    mem[0x004] = 0x00; mem[0x005] = 0x00;

    // 0x100  函数开始
    // 0x8014 => add 寄存器1 到 寄存器0
    mem[0x100] = 0x80; mem[0x101] = 0x14;
    // 0x8014 => add 寄存器1 到 寄存器0
    mem[0x102] = 0x80; mem[0x103] = 0x14;
    // 0x00EE => RETURN
    mem[0x104] = 0x00; mem[0x105] = 0xEE;

    cpu.run();

    assert_eq!(cpu.registers[0], 45);

    println!("5 + (10 * 2) + (10 * 2) = {}", cpu.registers[0]);

}

当你深入了解系统文档后，你会发现真实的函数比仅仅只是简单的跳转到一个预定义的内存更加复杂，操作系统以及CPU架构在调用规则以及能力上都有不同，有时操作需要被添加到栈中，又是它们需要被插入到预定义好的寄存器上。虽然具体的机制可能不同，但大体上都和刚刚你看到的类似，庆祝一下吧，你已经走了这么远！

CPU4：添加剩余部分

通过添加一些额外的操作码，我们可以在你的CPU上实现乘法以及更多的功能。Check the source code that comes along with the book, specifically the ch5/ch5-cpu4 directory at https://github.com/rust-in-action/ code for a fuller implementation of the CHIP-8 specification.

学习CPU以及数据的最后一步时理解控制流是如何工作的。在CHIP-8中，控制流通过判断寄存器中的值来实现，然后，根据输出修改position_in_memory。CPU中没有while和for循环，在编程语言中创建它们是编译器编写者的艺术。

总结

• 一个相同的位模式可以表示不同的值，取决于它的数据类型
• Rust标准库中的整数类型具有固定宽度，尝试增加到超过最大值会产生一个叫整数溢出的错误，递减到低于最小值会出现整数下溢（integer underflow）
• 通过在编译程序时开启优化（比如通过cargo build --release），可能让你的程序在运行时检查关闭的情况下出现整数溢出和整数下溢
• 字节顺序代表多字节类型中的字节布局，每一个CPU厂商都会决定它芯片组的字节顺序，一个为小端法CPU编译的程序在大端法CPU上运行会出现错误
• 小数类型主要通过浮点数类型标识。Rust的f32和f64遵循了IEEE 754标准，这些类型也被常称作单精度浮点数和双精度浮点数。
• f32和f64中，一样的位模式可能被比较为不相等，例如：f32::NAN != f32::NAN，并且不一样的位模式可能被比较为相等，比如-0 == 0。因此，f32和f64只满足部分等价关系（PartialEq），程序员需要在比较浮点值时留心。
• 在操作数据结构内部时，位运算非常有用，然而，做这些可能极其不安全。
• 定点数格式也可以使用，这些数的表示方式是将一个作为分子，另一个作为分母。
• 实现std::convert::From当你想要提供类型转换时。但是，在当类型转换可能失败时，选择std:convert::TryFrom更好
• 一个CPU操作码是一个数字，代表指令而不是数据，内存地址也只是一个数字，方法调用也只是一系列数字。